
当HP読者のHN「数er」さんからの出題です。(平成24年12月18日付け)
正五角形と正三角形の角度の問題は天下り的な方法以外で答えを求めることはできるの
でしょうか?できるのなら教えてください。お願いします。
例えば、「補助線の練習その2」の問題6とかです。天下り的にはできるのですが...。
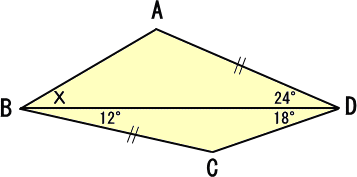
(答) らすかるさんが考察されました。(平成24年12月18日付け)
△ABDを裏返して、その裏返した三角形の辺DAと△BCDの辺BCをくっつけると頂角が36°
の二等辺三角形が出来ます。
この二等辺三角形に外接する正五角形を描き、Aと正五角形の1頂点を結ぶと、問題の角
度がわかります。問題6の答えは、30°だと思います。
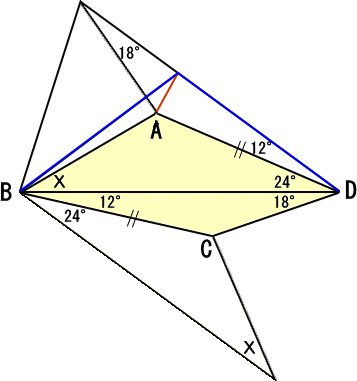
# 私は「この手の問題は必ず天下り的でない解き方が存在する」と思っています。
two-well さんからのコメントです。(平成27年3月20日付け)
8年ぐらい前に、「三角形の最大数」で書き込みさせていただきました。ネットで話題になっ
ていた幾何の問題を考えていたら、上記のような、私が見つけた解法と異なるものが掲載さ
れていました。過去の話題で今更という感じがしますが、その当時は「天下り的ではない解
法」を探されていたようですので、僭越ながら、ご紹介したいと思います。
以下のように補助線を描いて考えました。
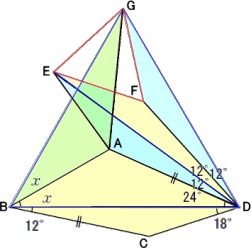
合同な三角形を3つ加えると、2つの正三角形
△BDG と △EFG
が出てきます。
2x=60°より、 x=30°
(コメント) two-well さん、お久しぶりです。なるほど!絵的に美しいですね。x の値が30°
ということが一目瞭然です。two-well さんに感謝します。