下図のように、２つの直角三角形が重なっている。
ＡＢ＝４、ＡＥ＝２、ＥＣ＝６、ＣＤ＝２ のとき、∠ＣＦＥの大きさを求めよ。
（答） １３５°
実際に、下図において、∠ＡＣＢ＝φ、∠ＤＥＣ＝θ とおくと、ｔａｎφ＝１/２、ｔａｎθ＝１/３
このとき、ｔａｎ（θ＋φ）＝（ｔａｎθ＋ｔａｎφ）/（１−ｔａｎθｔａｎφ）＝（１/３＋１/２）/（１−１/６）＝１
より、 θ＋φ＝４５° よって、 ∠ＣＦＥ＝１８０°−４５°＝１３５° （終）
三角関数を使わずとも、次のように考えれば、初等的に解くことが可能である。
△ＤＣＥ≡△ＥＡＥ’ となるように、点Ｅ’を定める。このとき、△ＥＤＥ’は、∠ＤＥＥ’＝９０°
の直角２等辺三角形となる。よって、∠ＥＤＥ’＝４５°となる。
さらに、ＢＣ
Ｅ’Ｄ なので、 ∠ＥＦＢ＝∠ＥＤＥ’＝４５°となる。したがって、∠ＣＦＥ＝１８０°−４５°＝１３５° （終）
よおすけさんから別解をいただきました。（令和６年７月１０日付け）
別の視点で挙げてみました。
（別解） 与えられた図のうち、△ＣDＥを平行移動させ、△ＧＨＣを作る。
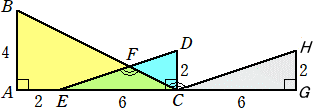
ＥD//ＣH、∠ＣＦＥ＝∠DＦＢ＝∠HＣＢ となるので、「角の大きさ(35)」の冒頭の図と同様
になる。
ＢＣ2＝４2＋８2＝８０ 、ＣＨ2＝２2＋６2＝４０ 、ＢＨ2＝２2＋１４2＝２００ より、
ｃｏｓ∠ＨＣＢ＝（８０＋４０−２００）/（８０
）＝−１/ なので、 ∠ＨＣＢ＝１３５°よって、∠ＣＦＥ＝１３５° （終）
（コメント） 「角の大きさ(35)」の類題になるとは、気がつきませんでした。よおすけさんに
感謝します。
以下、工事中！