
当HPがいつもお世話になっているHN「よおすけ」さんからの出題です。
(令和6年5月4日付け)
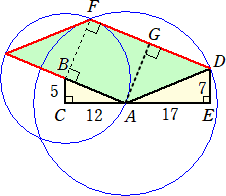
下図において、角θの大きさを求めよ。
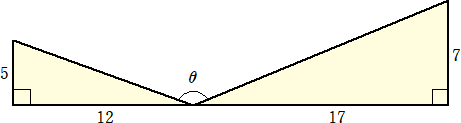
(答) θ=135°
実際に、線分BAを延長して、Dより垂線DFを引き、線分AEとの交点をGとおく。
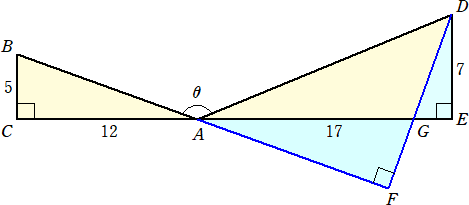
△ABC∽△AGF 、△AGF∽△DGE なので、 GE=(7/12)×5=35/12
よって、 AG=17−35/12=169/12 より、 AF=(169/12)×(12/13)=13
ここで、 AD2=172+72=338 より、 AD=13
よって、 DF=13 となり、△AFDは、AF=FDの直角2等辺三角形となる。
したがって、 ∠DAF=45° から、θ=180°−45°=135° (終)
(コメント) 点と直線の距離の公式を用いるなど、解き方は種々考えられる。
(別解1) AB=13 、AD2=172+72=338=2・169 より、 AD=13
BD2=292+22=845=5・169 より、 BD=13
余弦定理より、
cosθ=(AB2+AD2−BD2)/(2AB・AD)=(169+338−845)/(338
なので、 θ=135°
(別解2) Aを座標軸の原点とし、CEを x 軸にとると、直線BAの方程式は、
y=−(5/12)x すなわち、 5x+12y=0
D(17,7)と直線 5x+12y=0 との距離DFは、
(5・17+12・7)/√(52+122)=169/13=13
また、AD2=172+72=338=2・169 より、 AD=13
よって、 AF2=AD2−DF2=338−169=169 より、 AF=13
以上から、△AFDは、AF=FDの直角2等辺三角形となる。
したがって、 ∠DAF=45° から、θ=180°−45°=135°
カルピスさんからのコメントです。(令和6年5月6日付け)
θ=135°のとき、∠B+∠D(∠ADE)=135°で合ってますでしょうか?
(コメント) (90°−∠B)+(90°−∠ADE)+θ=180° から、
∠B+∠ADE=θ=135°
で、合っていますね!
カルピスさんからのコメントです。(令和6年5月7日付け)
問題から、少し外れますが、
2つの「直角三角形同士」が、この「向き」で接していた時、辺の長さが分かっていなくても
必ず、 ∠θ=∠B+∠D が成り立つ・・・ と、ちょとした公式(大げさ?)の出来上がりに
なるかな?中学入試問題にちょうどいい。
θが135°の時、∠Bと∠Dの和は何度ですか?(直感で、すぐに分かってしまうと思うけど)
(コメント) 点Aで垂線を立てれば、平行線の錯角の関係から明らかでしょう。
DD++ さんからのコメントです。(令和6年5月7日付け)

△ABC を、A を中心に時計周りに 90° 回転させてから外周が長方形になるよう補助線を
引くと、長方形から3つの直角三角形(うち、2つは合同)を切り落として直角二等辺三角形
が残る図ができます。
よって、 θ−90°=45°より、θ=135°
という解答が一番お手軽ですかね。
#直角三角形2つで、直角を挟む2辺の長さが
12+5=17 、12-5=7 、17+7=24=12*2 、17-7=10=5*2
みたいな関係のときには、まず、この図を作ることを考えるようにしています。
(コメント) なるほど、上手く、直角2等辺三角形が作れるんですね!気がつきませんでした。
DD++ さんに感謝します。
よおすけさんから別解をいただきました。(令和6年5月7日付け)
別解を見つけたので紹介。
与えられた図で、2辺が 5、12 の直角三角形を、BC=5、CA=12、∠ACB=90°の
△ABC、2辺が 7、17 の直角三角形を、DE=7、AE=17、∠AED=90°の△ADEとする。
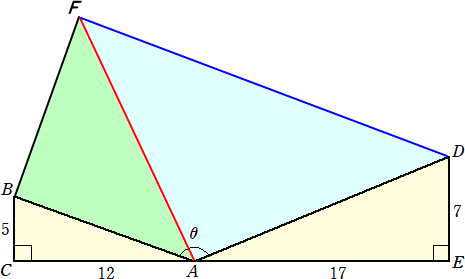
点Bを中心とし、反時計回りに点Aを90°回転させた点と、点Aを中心とし反時計回りに
点Dを90°回転させた点は、AD=AF=13
AD=AF および ∠DAF=90°
また、これによりできた△FBAは、AB=BF、∠AFB=∠BAF=45°で、∠ABF=90°の
直角二等辺三角形。よって、θ=∠BAF+∠DAF=135°
(コメント) よおすけさんからいただいた別解を若干補正させていただきました。趣旨が合う
ようにしたつもりですが、よおすけさん、これで合っていますか?
よおすけさんからのコメントです。(令和6年5月8日付け)
はい。おおむね挙げた通りです。そういえば、もう1つ解答をつくりました。
Aを中心とし、ADを半径とする円、Bを中心とし、ABを半径とする円を描き、2円の交点をF
とする。ABを延長し、円との交点をGとする。
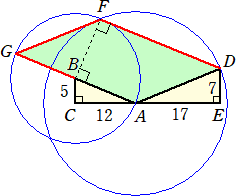
このとき、AD=AF=GF=13
直角2等辺三角形BFGにおいて、∠AGF=45°となる。
AD//GFより、θ+45°=180° なので、 θ=135゜ (終)
#三平方の定理を使わずに角θを割り出せる解法ないかな...と思って投稿しました。
(コメント) 「平行四辺形FGAD」がこの解答のキーワードですが、それを示すために、どうし
ても三平方の定理は必要で、三平方の定理の呪縛からは逃れられないと思います。
よおすけさんからさらなる別解をいただきました。(令和6年5月10日付け)
上記と冒頭は同じですが、別解がまたできたので紹介。
Aを中心とし、ADを半径とする円、Bを中心とし、ABを半径とする円を描き、2円の交点をF
とする。この時、∠DAF=90°
点Aから辺DFへ垂線を引き、その交点をGとする。
このとき、∠BAG=90°で、∠DAG=∠FAG=45°
また、∠DAF=90°、∠FAG=45°より、∠BAF=45°
∠BAF、∠FAG、∠DAGはいずれもθの1/3に等しいので、θ=135° (終)
(コメント) ∠BAG=90°、∠DAG=45°から、θ=135°とした方が速いかな?
以下、工事中!