角の大きさ（３）　　　　　　　　　　　　　　　　　　　　　　　　　　　

　下図の△ＡＢＣにおいて、辺ＢＣの下方に△ＤＢＣを作る。

ただし、∠ＢＣＤ＝２０°で、さらに、　ＡＢ＝ＣＤ　とする。

　　　　　　　

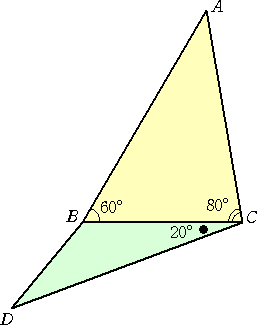
　このとき、∠ＤＢＣ は何度になるであろうか？　

　　　　　　　　　　　　　　　　　　　　　　　　　　　（大阪清風高校数学オリンピック問題より）



















（答）　１３０度である。

　そのままの図形で角度を求めることは、多分難しい．．．。

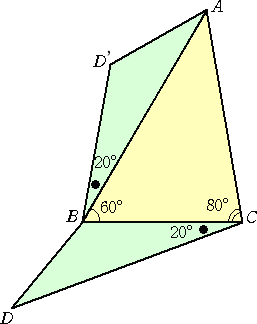　左図のように、下側の三角形と合同な三角形を
左側に貼り付けて考えると、考えやすいかもしれ
ない。

　このとき、左図の上側の四角形ＡＤ’ＢＣは、

当ＨＰの「角の大きさ（２）」で考えたものになる。

　その結果を用いれば、　

　　　∠ＢＡＤ’＝∠ＢＤＣ＝３０°　なので、

　　∠ＤＢＣ＝１３０°となる。








　清風高校の生徒さんの解答を参考にすると、次のような別解も可能となる。

左図のように、四角形ＡＢＣＥ が平行四辺形となるように点Ｅ をとる。 　次に、∠ＢＡＣの２等分線上に ＡＥ＝ＡＦ　となる点Ｆをとる。 　このとき、△ＡＥＦは２等辺三 角形となり、∠ＥＡＦ＝１００° よって、∠ＡＦＥ＝∠ＡＥＦ＝４０° このとき、 　　　∠ＦＥＣ＝∠ＦＡＣ＝２０° なので、４点 Ａ、Ｅ、Ｃ、Ｆ は同 一円周上にある。

　このことから、∠ＥＣＦ＝８０°で、∠ＥＣＡ＝４０°より、　∠ＦＣＡ＝４０°となる

したがって、線分ＦＣは∠ＡＣＢの２等分線となり、点Ｆは△ＡＢＣの内心となる。

　よって、　∠ＡＢＦ＝３０°となる。

　△ＡＢＦと△ＣＤＦにおいて、

　　　ＡＢ＝ＣＤ　、　ＡＦ＝ＡＥ＝ＣＢ　、　∠ＦＡＢ＝∠ＢＣＤ＝２０°

なので、２辺とその間の角相等から、　△ＡＢＦ≡△ＣＤＦ　となる。

　以上から、　∠ＤＢＣ＝∠ＢＦＡ＝１８０°−２０°−３０°＝１３０°　となる。　（終）