孅愜偡傞棟桼丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂偄偮傕夛崌偵巊偭偰偄傞強偑巊偊偢丄崱擔乮俀侽侽俁丏俉丏侾俉乯偼丄墶昹儔儞僪儅乕僋僞儚乕偵
夛応傪堏偟偰夛崌傪傕偭偨丅挬偐傜塉柾條偱丄嶗栘挰墂傪偍傝偰摦偔曕摴慜偱儔儞僪儅乕僋僞
儚乕傪尒忋偘偨傜丄拞憌奒埵偐傜塤偱偡偭傐傝暍傢傟偰偄偰丄嵟忋奒偑尒偊側偐偭偨丅傕偟丄
惏傟偰偄偨傜丄嵟忋奒偺揥朷幒偵峴偭偰乮桳椏乯丄墶昹偺宨娤傪妝偟傕偆偲寁夋偟偰偄偨偑丄
巆擮側偑傜弌棃側偐偭偨丅
丂夛崌偺媥傒帪娫偵丄傆偲偟偨偙偲偑偒偭偐偗偱丄乽側偤丄岝偼孅愜偡傞偺偐丠乿偲偄偆偙偲偑
榖戣偵側偭偨丅悢妛揑偵傕嫽枴偁傞僥乕儅側偺偱丄偙偙偱丄傑偲傔偰偍偒偨偄偲巚偆丅
丂岝偼丄俀偮偺堎側偭偨攠幙偺嫬奅柺偵摓払偡傞偲丄堦斒偵偼偦偺嫬奅柺偱曽岦傪曄偊偰
恑傓丅偙傟偑丄岝偺孅愜偲偄偆尰徾偱偁傞丅
丂偙偺傛偆側尰徾偼丄悈偺擖偭偨僐僢僾偺拞偵敘傪擖傟偨偲偒偲偐偱傕娤嶡偡傞偙偲偑偱偒傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂
丂偄偔偮偐尵梩傪妋擣偟傛偆丅
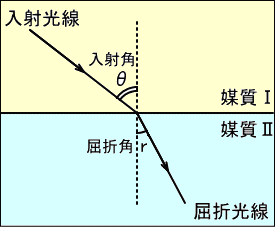 丂丂嵍恾偵偍偄偰丄
丂丂嵍恾偵偍偄偰丄
丂丂乮侾乯丂擖幩岝慄偲孅愜岝慄偼摨堦暯柺忋丅
丂丂
丂丂乮俀乯丂擖幩妏偲孅愜妏偺惓尫斾偼堦掕丅
丂丂丂丂丂乮斾椺掕悢傪丄乮憡懳乯孅愜棪偲偄偆丅乯
丂丂偑尵偊傞丅乮孅愜偺朄懃乯
丂丂丂偙偺孅愜偺朄懃偼丄俽値倕倢倢 偵傛傝丄侾俈悽
丂丂婭弶摢偵敪尒偝傟偨丅
丂丂攠幙嘥傪嬻婥乮恀嬻乯偲偟偨偲偒丄攠幙嘦偑悈偺応崌偺孅愜棪偼丄戝懱丂係/俁
偖傜偄
丂僈儔僗偺応崌偼丄戝懱丂俁/俀 偖傜偄偱偁傞丅
丂岝偺孅愜偼丄偳偆偟偰婲偙傞偺偐丄偦偟偰丄孅愜偺朄懃乮俀乯偼側偤惉傝棫偮偺偐丄側偳偼丄
幚偼丄師偺儂僀僿儞僗乮俫倳倷倗倕値倱乯偺尨棟偵傛偭偰愢柧偝傟傞丅
丂偙偺尨棟偼丄岝偼攇偱偁傞偲偄偆棫応偱弎傋傜傟傞丅乮儂僀僿儞僗偺攇摦愢乯
忋婰偱弎傋偨孅愜偺朄懃偼丄宱尡揑朄懃偱偁傞偑丄偙偺朄懃傪崌棟揑偵愢柧偡傞偨傔偵丄
儂僀僿儞僗偼丄偙偺尨棟傪採彞偟偨丅乮侾俇俈俉擭乯
丂侾俉侽俈擭偺儎儞僌偺姳徛幚尡偵傛傝丄岝偺攇摦惈偑妋擣偝傟偰偄傞丅
丂丂丂丂丂丂丂丂丂丂丂乮嶲峫暥專丗彫郪廏梇丂挊丂岝妛偲娽壢婡婍偐傜枹棃傊丂乮妛巑夛夛曬乯乯
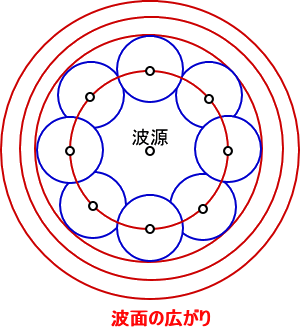
丂丂儂僀僿儞僗乮俫倳倷倗倕値倱乯偺尨棟
丂 丂攇偼攇尮偐傜攠幙傪捠偟偰揱斃偝傟傞偑丄
丂丂侾偮偺攇柺忋偺慡偰偺揰偼丄怴偨側攇尮
丂丂偲側偭偰丄摨偠懍搙丄摨偠怳摦悢偺彫攇傪
丂丂弌偡丅屄乆偺彫攇偼娤應偝傟偢丄偙傟傜
丂丂偺彫攇偺攇柺偵嫟捠偵愙偡傞嬋柺偑丄偦
丂丂偺屻偺攇柺偲偟偰娤應偝傟傞丅
丂丂丂攇偺恑峴曽岦偼攇柺傪悅捈偵偮側偄偩
丂丂慄偵側傞丅
丂偙偺儂僀僿儞僗偺尨棟傪梡偄傟偽丄攇偺揱斃懍搙偺曄壔偲偟偰丄孅愜偺婲偙傞棟桼偑愢柧
偝傟傞丅
丂堦斒偵丄攇尮偵懳偟偰丄偦偺攇柺偼媴柺乮媴柺攇乯偱偁傞偑丄攇尮偑廫暘墦偔偵偁傞丄傑偨偼丄
攇柺偺廫暘彫偝偄晹暘偱峫偊傞偲偡傟偽丄攇柺偼暯柺乮暯柺攇乯偱偁傞偲偟偰傛偄丅
丂丂丂丂丂丂丂丂丂丂丂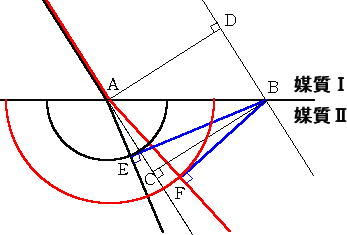
丂忋恾偼丄岝偑嫬奅柺忋偺揰俙偵払偟偰偐傜丄俙偲摨偠攇柺忋偵偁偭偨揰俢偑嫬奅柺忋偺揰俛
偵払偡傞傑偱偺攇偺揱斃偺條巕傪柾偟偨傕偺偱偁傞丅
丂忋恾偐傜暘偐傞傛偆偵丄攠幙嘦偵偍偗傞攇偺揱斃懍搙偑丄攠幙嘥偵偍偗傞傕偺偲摨偠側傜偽丄
揰俙偼揰俠偵揱傢傝丄孅愜偼婲偙傜側偄丅
丂偙傟偵懳偟偰丄攠幙嘦偵偍偗傞攇偺揱斃懍搙偑丄抶偗傟偽丄揰俤偵揱傢傝丄懍偗傟偽丄揰俥
偵揱傢傝丄柧傜偐偵孅愜偟偰偄傞丅徻偟偔偼丄墌偲愙慄偺娭學偵傛傝愢柧偝傟傞丅
丂偄傑丄孅愜岝慄偑捈慄俙俤偺応崌傪峫偊傞丅
擖幩妏傪 兤丄孅愜妏傪 倰 偲偡傞偲丄忋恾偵偍偄偰丄佢俛俙俢亖兤丄佢俙俛俤亖倰 偱偁傞偺偱丄
丂丂丂丂丂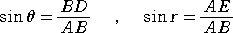
丂丂丂傛偭偰丄
丂丂丂丂丂丂丂丂丂丂丂丂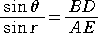
丂丂奺攠幙拞偺攇偺揱斃懍搙偼堦掕側偺偱丄忋幃偺塃曈偼掕悢偲側傞丅
丂偟偨偑偭偰丄擖幩妏偲孅愜妏偺惓尫斾偼堦掕偱偁傞偙偲偑帵偝傟偨丅
丂嬻婥拞偲悈拞偲偺懍偝傪斾傋傞偲丄岝偼悈拞偺曽偑抶偔丄壒偼悈拞偺曽偑懍偄丅
丂偟偨偑偭偰丄岝偑嬻婥拞偐傜悈偺拞傊恑傓偲偒丄忋恾偱尵偊偽丄揰俙偐傜揰俤傊帄傞婳愓傪
昤偔偙偲偵側傞丅傑偨丄僾乕儖偱悈拞偵愽偭偰偄傞偲偒丄妱偲嬤偔偱悈忋偐傜惡傪妡偗傜傟偰傕丄
墦偔偐傜偺傕偺偲姶偠傜傟傞偲偄偆偙偲偵傕崌揰偑偄偔丅
丂偲偙傠偱丄朻摢偺僐僢僾偺拞偺敘偼丄悈拞晹暘偑晜偒忋偑偭偰尒偊傞丅
偙傟偼丄師偺傛偆偵愢柧偝傟傞丅
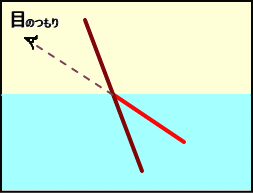 丂丂丂岝慄媡恑偺尨棟偐傜丄悈拞晹暘偺敘偼丄嵍恾偺
丂丂丂岝慄媡恑偺尨棟偐傜丄悈拞晹暘偺敘偼丄嵍恾偺
丂丂傛偆偵孅愜偟偰丄栚偵払偡傞丅偙偺偲偒丄恖娫偺擼
丂丂偼丄栚偵擖偭偰偒偨岝慄偺曽岦偐傜丄偦偺墑挿慄
丂丂忋乮愒偄晹暘乯偵敘偺愭偑偁傞傕偺偲嶖妎偡傞丅
丂丂偦傟偱丄悈拞晹暘偑晜偒忋偑偭偰偄傞傛偆偵尒偊
丂丂偨傢偗偱偁傞丅
乮嶲峫暥專丗嬥尨庻榊丂挊丂暔棟偺尋媶乮墵暥幮乯
丂丂丂丂丂丂丂椡晲忢師丒杒懞椙晇丒惔悈岝帯丂挊丂暔棟嘥丒嘦乮悢尋弌斉乯乯
乮捛婰乯丂岝偵懳偡傞僼僃儖儅乕乮1601乣1665乯偺峫嶡偐傜丄岝偼捠夁偵梫偡傞嫍棧偑嵟彫偲
丂丂丂丂側傞傛偆側宱楬偵増偭偰恑傓丅偙偺偙偲傪妋擣偟偰傒傛偆丅
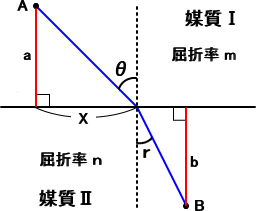 丂丂嵍恾偺傛偆偵丄俀揰俙丄俛傪岝偑捠夁偡傞応崌傪
丂丂嵍恾偺傛偆偵丄俀揰俙丄俛傪岝偑捠夁偡傞応崌傪
丂峫偊傞丅俙俛娫偺悈暯嫍棧傪 俴 偲偡傞偲丄岝偺宱
丂楬偺岝妛嫍棧 俵 偼丄
丂丂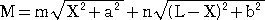
丂偺嵟彫抣偵傛傝梌偊傜傟傞丅幚嵺偵丄
丂丂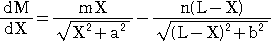
丂丂偙偺偲偒丄
丂丂丂丂丂丂丂丂丂丂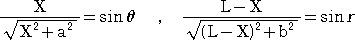
丂丂側偺偱丄
丂丂丂丂丂丂丂丂丂丂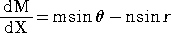
| 丂丂偲偙傠偱丄孅愜偺朄懃 |
丂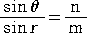 |
丂偑惉傝棫偮偲偒丄 |
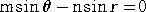 |
丂丂側偺偱丄
丂丂丂丂丂丂丂丂丂丂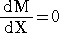
丂丂偲側傞丅傑偨丄擟堄偺倃偵偍偄偰丄
丂丂丂丂丂丂丂丂丂丂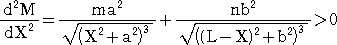
丂丂偑惉傝棫偮丅
丂丂埲忋偐傜丄孅愜偺朄懃偑惉傝棫偮岝偺宱楬偵偍偄偰丄俵偼嬌彫偐偮嵟彫偲側傞丅
丂偙偺偙偲傪丄媡偵峫偊傟偽丄俵偑嵟彫偲側傞傛偆側宱楬傪岝偑捠夁偡傞偲偒丄帺慠偵孅愜
偺朄懃偑惉傝棫偮偙偲偵側傞丅
乮嶲峫暥專丗屗揷惙榓丂挊丂嵟彫尨棟乮悢妛侾侽侽偺栤戣傛傝乯丂乮擔杮昡榑幮乯乯
乮捛乆婰乯丂岝偺孅愜丒斀幩偵偮偄偰丄戝曄嬃偔傋偒帠幚偑夝柧偝傟偨丅
丂崱傑偱丄岝偺擖幩抧揰偲摨偠応強偐傜丄斀幩丒孅愜偟偰偄傞偲峫偊傜傟偰偒偨偑丄帠幚偼
堘偆偲偺偙偲偱偁傞丅嶻嬈媄弍尋媶強偲搶戝偺僌儖乕僾偺尋媶偵傛傝撍偒巭傔傜傟偨丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮挬擔怴暦俀侽侽係擭俋寧俋擔晅偗挬姧乯
丂丂丂丂丂丂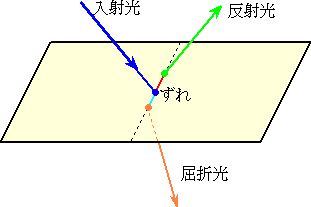
丂偢傟偼偛偔嬐偐偱丄岝妛惢昳乮儗儞僘側偳乯偱偼柍帇偱偒傞斖埻傜偟偄偑丄岝捠怣偵偼塭
嬁偑偁傞傜偟偄丅
乮捛婰乯丂暯惉俀俇擭俋寧侾俀擔晅偗
丂挿栰導棫斞嶳杒崅峑偺拞懞岞堦愭惗偑丄師偺栤戣偵庢傝慻傑傟偨丅偙偺暸偵娭楢偡傞
榖戣偱偲偰傕嫽枴偁傞栤戣偱偁傞丅
乮嶲峫暥專丗丂拞懞岞堦丂挊丂乽晜偒忋偑傝嬋慄乿丂乮悢尋捠怣丂俶倧丏俉侽丂乮悢尋弌斉乯乯乯
丂僾乕儖偺掙柺偵堷偐傟偨儔僀儞偼丄墦偔偵峴偗偽峴偔傎偳忋偵晜偒忋偑偭偰尒偊傞偑丄
偙偺嬋慄偺曽掱幃偼偳偆側傞偺偩傠偆偐丠
丂寁嶼傪娙扨壔偡傞偨傔丄
丂丂丂悈柺傪倶幉偲偟丄僾乕儖偺掙柺偵堷偐傟偨儔僀儞偺曽掱幃傪丄倷亖亅侾
偲偡傞丅傑偨丄娤應幰偺栚偺埵抲傪丄俲乮侽丆倛乯偲偡傞丅
丂揰俹乮侽丆亅侾乯偐傜擖幩妏冇偱擖幩偟偨岝慄偼悈柺偱孅愜偟丄孅愜妏兤偲偡傞偲丄孅愜慄偺
曽掱幃偼丄
丂丂丂丂丂丂丂倷亖乮亅侾/倲倎値兤乯乮倶亄倲倎値冇乯
丂摨條偵丄
丂揰俹乮侽丆亅侾乯偐傜擖幩妏冇亄儮冇偱擖幩偟偨岝慄偼悈柺偱孅愜偟丄孅愜妏兤亄儮兤偲偡
傞偲丄孅愜慄偺曽掱幃偼丄
丂丂丂丂丂丂丂倷亖乮亅侾/倲倎値乮兤亄儮兤乯乯乮倶亄倲倎値乮冇亄儮冇乯乯
丂俀捈慄偺岎揰乮倶丆倷乯偺嵗昗偼丄
丂倶亖亅倲倎値冇亄倲倎値兤乮倲倎値乮冇亄儮冇乯亅倲倎値冇乯/乮倲倎値乮兤亄儮兤乯亅倲倎値兤乯
丂倷亖亅乮倲倎値乮冇亄儮冇乯亅倲倎値冇乯/乮倲倎値乮兤亄儮兤乯亅倲倎値兤乯
丂偙偙偱丄儮冇仺侽 偲偡傞偲丄儮兤仺侽 偱丄乮倶丆倷乯仺乮倶0丆倷0乯偲偡傞偲丄
丂倶0亖亅倲倎値冇亄倱倝値兤們倧倱2兤/乮値們倧倱3冇乯
丂倷0亖亅們倧倱3兤/乮値們倧倱3冇乯
丂偙傟偼丄擖幩妏冇丄孅愜棪兤偺孅愜慄忋偐傜尒偨応崌偺揰俹偺尒偐偗忋偺揰俥乮倶0丆倷0乯
偺嵗昗偲側傞丅
丂悈偺孅愜棪傪値偲偡傞偲丄孅愜偺朄懃偐傜丄丂倱倝値兤亖値倱倝値冇丂側偺偱丄忋幃偼丄
丂倶0亖亅乮値2亅侾乯倲倎値3冇
丂倷0亖亅乮侾/値乯乮侾亅乮値2亅侾乯倲倎値2冇乯3/2
偲傕彂偗傞丅偙傟傛傝丄冇傪徚嫀偡傞偲丄
丂丂倷0亖亅乮侾/値乯乮侾亅乮値2亅侾乯1/3倶02/3乯3/2
偨偩偟丄掕媊堟偼丄亅侾/併乮値2亅侾乯亙倶亙侾/併乮値2亅侾乯丂偱偁傞丅
丂偦偙偱丄栤戣偼丄揰俹偑捈慄 倷亖亅侾 忋傪摦偔偲偒丄孅愜慄偑娤應揰俲傪捠傞応崌偺尒偐偗
忋偺揰俥乮倶0丆倷0乯偑偳偺傛偆側婳愓傪昤偔偐偲偄偆偙偲偱偁傞丅
丂忦審傛傝丄揰俹偺倶嵗昗偼丄丂倛倲倎値兤亄倲倎値冇丂偲側傞偺偱丄揰俥傕暯峴堏摦偝傟偰丄
丂倶0亖倛倲倎値兤亄倱倝値兤們倧倱2兤/乮値們倧倱3冇乯
丂倷0亖亅們倧倱3兤/乮値們倧倱3冇乯
偲側傞丅
丂偄傑丄俲俥2亖倶02亄乮倛亅倷0乯2亖倰2丂偲偍偔偲丄丂倰倱倝値兤亖倶0丂丄倰們倧倱兤亖倛亅倷0丂側偺偱丄
丂乮値2亅侾乯倶02亖乮倛亅倷0乯2乮値4/3倷0(-2/3)亅値2乯
丂偟偨偑偭偰丄媮傔傞揰俥偺婳愓偺曽掱幃偼丄
丂丂乮値2亅侾乯倶2亖乮倛亅倷乯2乮値4/3倷(-2/3)亅値2乯丂丂偨偩偟丄悈偺孅愜棪値亖係/俁偱丄倷亙侽
丂悈柺偐傜偺嫍棧倛亖侾丏俉偲偟偰僌儔僼昤夋僜僼僩偵僌儔僼傪昤偐偣傞偲丄師偺傛偆偵側傞丅
丂丂丂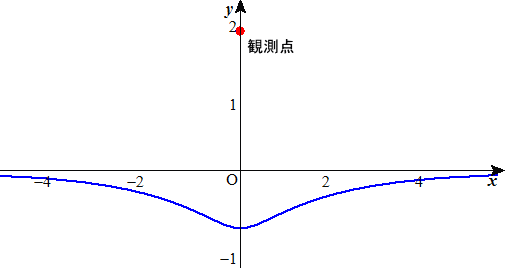
乮僐儊儞僩乯丂拞懞岞堦愭惗偺寢壥偵姶摦偟傑偟偨丅妋偐偵偙傫側晽偵尒偊偰偄傑偡傛偹両
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俇擭俋寧侾俀擔晅偗乯
丂忋婰傪攓尒偟偰丄傆偲崅峑帪戙偺媈栤傪巚偄弌偟傑偟偨丅偳側偨偐偙傟偵摎偊傜傟傞曽偑
偄傜偭偟傖偄傑偟偨傜偛嫵帵偔偩偝偄丅
丂悈柺傪x幉丄僾乕儖偺掙傪 y=-1 偲偟傑偡丅墱峴偼峫偊傑偣傫丅嬻婥拞偺岝偺懍偝傪1偲偟丄
悈偺孅愜棪偼娙扨偺偨傔2偲偟傑偡丅偡側傢偪悈拞偱偺岝偺懍偝傪1/2偲偟傑偡丅傑偨丄悈柺
偼廫暘偵壐傗偐偱偁傞偲偟傑偡丅
[1]丂悈柺偐傜堦搙奜偵弌傞応崌偲弌側偄応崌傪偦傟偧傟峫偊傞偙偲偱丄(4,-1) 偐傜 (0,-1) 傑
丂丂偱岝偑嵟抁偱撏偔宱楬傪尒偮偗偰偔偩偝偄丅
丂丂乮悢妛揑偵偼嵟抁偱側偔壓尷偲偄偆傋偒偐傕偟傟傑偣傫偑乯
[2]丂(4,-1) 偵揰岝尮傪抲偄偨応崌丄僼僃儖儅乕偺尨棟偵傛傟偽丄(0,-1) 偵偄傞娤應幰偼嬄妏
丂丂壗搙偵岝尮傪娤應偡傞偲峫偊傜傟傞偱偟傚偆偐丅
[3]丂揰岝尮傪 (5,-1) 偵傕抲偄偨応崌丄(0,-1) 偵偄傞娤應幰偼丄偙偺怴偟偄岝尮傪嬄妏壗搙偵
丂丂娤應偡傞偲峫偊傜傟傞偱偟傚偆偐丅
[4]丂偁傞応強埲墦偺掙慡懱傪岝傜偣傞偲壗傗傜戝曄側偙偲偵側傝偦偆偱偡偑丄偙傫側尰徾偼
丂丂壥偨偟偰尰幚偵婲偙傞偺偱偟傚偆偐丅婲偙傜側偄偺偩偲偡傞偲堦懱側偤丠
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俇擭俋寧侾俁擔晅偗乯
丂惓妋側抦幆傪帩偭偰傞帺怣偼側偄偱偡偑峫偊偰傒傑偟偨丅
丂僼僃儖儅乕偺尨棟偵傛傟偽丄乽抧揰A偐傜弌偨岝傪丄抧揰B偐傜娤應偟偨側傜偽丄偦偺岝妛
揑嵟抁宱楬偑帵偡曽岦偵岝偑娤應偝傟傞乿偲抦傜傟偰偄傞乮偐偲擣幆偟偰偄傑偡乯丅
丂偙偺庡挘偵俀偮拲堄揰偑偁傞偲峫偊傑偟偨丅
(a) 岝偺嫮偝偵偮偄偰
丂椺偊偽丄堜屗偺掙偵岝尮偑偁傞偲偟傑偡丅堜屗偺墶偵棧傟偰棫偭偰偄傞娤應幰偐傜偼岝尮
偼捈姶揑偵尒偊傑偣傫丅偟偐偟丄堜屗偺掙偐傜娤應幰偵岦偐偆嵟抁宱楬乮愜傟慄乯偼懚嵼偟
傑偡丅偍偦傜偔丄偦偺宱楬偺岝偼懚嵼偟側偄偙偲偼側偄乮夞愜乯偗傟偳旝庛側偺偱偟傚偆丅
丂偙偺傛偆偵丄僼僃儖儅乕偺尨棟偼岝偺嫮偝傪昡壙偟傑偣傫丅偦傟傪昡壙偡傞偵偼暿偺寢壥
偑昁梫偵側傝傑偡丅乮僼儗僱儖夞愜偲偄偆幃偑偁傞傛偆偱偡偑擄偟偔偰暘偐傝傑偣傫乯
(b) 懠偺宱楬傪捠偭偨岝傕娤應偝傟傞偙偲偵偮偄偰
丂嬀偺慜偱帺暘偺庤傪尒傞帪偵偼捈愙尒偊傞偺偵壛偊偰丄嬀偵塮偭偰偄傞偺傕尒偊傞偱偟傚
偆丅嵟抁宱楬傪嬌彫宱楬偲偐尵偄捈偡偲椙偄偐傕偟傟側偄偲巚偄傑偟偨丅
丂採帵偝傟偨栤戣傪峫偊傞嵺偵傕偆侾偮偺廳梫偲巚傢傟傞偙偲偱丄岝偑悈柺偵摉偨傞帪丄斀
幩岝偲孅愜岝偵暘偐傟傑偡丅偦偺嵺偺摟夁偲斀幩偺妱崌偵娭偟偰丄僼儗僱儖偺幃偑抦傜傟
偰偄傑偡丅寢壥偵偼丄孅愜岝偑悈柺偡傟偡傟乮孅愜妏兝偑90搙乯偵嬤偯偔偵偮傟偰丄斀幩岝
偺妱崌偑侾偵丄孅愜岝偺妱崌偑侽偵嬤偯偒傑偡丅
丂悈柺偡傟偡傟偺岝偼嵟抁宱楬偱偼偁傞偗傟偳傕旝庛側岝偵側傞偺偱偼側偄偐偲峫偊傑偡丅(a)
偦傟埲奜偵丄揰岝尮偐傜捈恑偟偰偔傞岝偲丄悈柺偱斀幩偟偰偔傞岝偑娤應偝傟傞偲巚偄傑偡丅(b)
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俇擭俋寧侾俁擔晅偗乯
丂側傞傎偳丄妋偐偵2夞偺孅愜偲偟偰嫮搙昡壙偡傞偲0廂懇偟傑偡偹丅柍尷偵峀偄岝尮傪梡堄
偟偰傕0廂懇偐崅乆桳尷廂懇偟偦偆偱偡丅偛夞摎偄偨偩偒偁傝偑偲偆偛偞偄傑偡丅
丂暿宱楬偐傜撏偔岝偑偁傞偙偲偵偮偄偰偼擣幆偟偰偄傑偟偨偑丄偙傟偵偮偄偰傕媈栤偑1偮巆偭
偰偄傑偡丅
丂捈愙岝偵偮偄偰偼嬌彫宱楬偲偄偆偙偲偱擺摼偡傞偲偟偰丄(2,0) 偱慡斀幩偟偰偔傞宱楬偼偄傢
偽埰揰偺傛偆側傕偺偱偁偭偰嬌彫偱偼側偄偲巚偄傑偡丅偦傟偱傕偙偺宱楬偺岝偑撏偔偺偼側偤
側偺偱偟傚偆偐丅
丂嬻廙偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俇擭俋寧侾係擔晅偗乯
丂嬌彫偲尵偆尵梩傪埨堈偵巊偭偰偟傑偭偨偐傕偟傟傑偣傫丅宱楬偑嬌彫偱偁傞偲偼偳偆偄偆偙偲
偐傪峫偊偰傒傞偲丄偦傟傎偳娙扨偱偼側偄傛偆偵巚偄傑偟偨丅傑偨峫偊偰傒傑偡丅


 丂丂嵍恾偵偍偄偰丄
丂丂嵍恾偵偍偄偰丄

 丂丂丂岝慄媡恑偺尨棟偐傜丄悈拞晹暘偺敘偼丄嵍恾偺
丂丂丂岝慄媡恑偺尨棟偐傜丄悈拞晹暘偺敘偼丄嵍恾偺 丂丂嵍恾偺傛偆偵丄俀揰俙丄俛傪岝偑捠夁偡傞応崌傪
丂丂嵍恾偺傛偆偵丄俀揰俙丄俛傪岝偑捠夁偡傞応崌傪
