質問に対する回答（７）　　　　　　　　　　　　　　　　　　

　平成１７年４月４日　当ＨＰの掲示板「出会いの泉」に、two-well 様から質問があった。

質問内容

　積分

　

の値を求めよ。

（置換積分による解法）　　ｘ＝ｔａｎθ　とおくと、ｄｘ＝（ｔａｎ²θ＋１）ｄθ

　このとき、

　

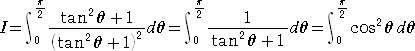
　ここで、

　

なので、

　

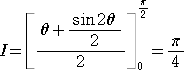
である。

（留数計算による解法）

　

として考える。

　ｚ を複素数として、

　

とおく。このとき、　ｚ＝ｉ　は、上半平面における唯一の特異点で、２位の極である。

留数を求めると、

　

である。

したがって、 ｒ＞１　として、実軸上の区間 ［−ｒ ，ｒ ］ と 半径 ｒ の上半円 Ｃ_ｒ で結ばれる曲

線 Ｃ に対して、

　

が成り立つ。ここで、

　

において、　 Ｃ_ｒ ：｜ｚ｜＝ ｒ　より、

　

なので、

　

以上から、　２Ｉ ＝ π/２　　となり、　Ｉ ＝ π/４　である。


（コメント）　two-well 様、このような解答でいかがでしょうか？