
平成17年3月11日 当HPの掲示板「出会いの泉」に、いつもお世話になっている未菜
実さんから質問があった。
質問内容
19×19 のマス目に、1×5 のタイルを敷詰める。19×19=361≡1 (mod 5) なので、
1マスどこかに穴があくはず! その穴の位置はどこだろうか?
未菜実さんによれば、
1×n のタイルを、m×m (ただし、m=p×n−1 、p、n は自然数)のマス目に敷詰める
場合、n が奇数の場合は既に解は判明しているが、n が偶数の場合は、まだ不明とのこと
である。
上記の問題を理解するために、次の例題を考えてみることにした。
例題 9×9 のマス目に、1×5 のタイルを敷詰める。穴の位置はどこだろうか?

のマス目に、
を埋め込む問題の常套的手段は、未菜実さんもやられているように、1×5 のタイルの5ヶ
所に異なる番号が割り振られるように9×9 のマス目に番号を割り振ることである。
1×5 のタイルをどのようにおいても上記の条件を満たすためには、次のように番号を割
り振ればよい。
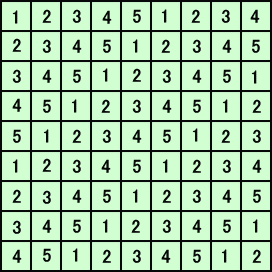
上記の表で、1、2、3、5 の番号は、何れも 16個で、4 の番号のみが 17 個ある。
1×5 のタイルには、全ての番号が均等に用いられるので、4 の番号のみが 1 個余る。
今、9×9 のマス目に、1×5 のタイルが敷き詰められ、4 の番号のどれかに穴があい
ているとものとする。
そのとき、その敷き詰められた状態を対称移動しても、同様にタイルが敷き詰められて、
どこかに穴があいているはずであるが、上記の理由から、その場所には、4 の番号が割
り振られていなければならない。
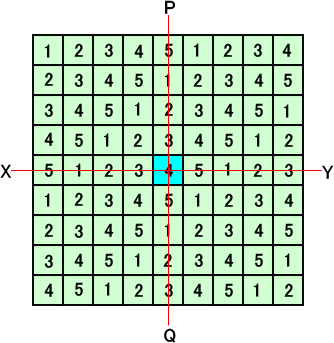
上図で、X−Y軸、P−Q軸に関する対称移動で所要の条件を満足する場所は中央の1ヶ
所のみである。(これは、あくまでも敷き詰められたとしたときの必要条件であり、十分条件
ではない。)
次に、上記の場所に穴があくことの十分性を確認しよう。そのためには、実際に、そのよう
な敷き詰め方を構成すればよい。
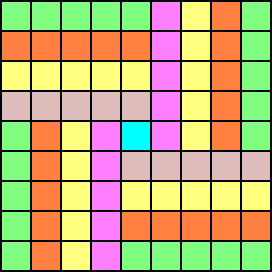
上記のような敷き詰め方が存在するので、上記で得られたことは十分条件にもなっている。
一般に、1×n のタイルを、m×m (ただし、m=p×n−1 、p、n は自然数)のマス目に
敷詰めるとき、 m≡−1 ( mod n )なので、上記と同様に番号を割り振れば、番号 n−1
が常に他の番号よりも 1 個多くなる。このことは、簡単に次のようにして確かめることがで
きる。
1 ≦ k ≦ n−2 のとき、 番号 k は、
k+(n+k)+(2n+k)+・・・+((p−1)n+k)
+(pn−(k+2))+((p−1)n−(k+2))+・・・+(n−(k+2))
=2(n+2n+・・・+pn)−pn−2p=p(p+1)n−pn−2p=p2n−2p (個)
ある。
k = n−1 のとき、 番号 n−1 は、
n−1+(n+(n−1))+(2n+(n−1))+・・・+((p−1)n+(n−1))
+(pn−(n+1))+((p−1)n−(n+1))+・・・+(2n−(n+1))
=2(n+2n+・・・+pn)−pn−n−2p+n+1=p(p+1)n−pn−2p+1
=p2n−2p+1 (個)
ある。
k = n のとき、 番号 n は、
n+(n+n)+(2n+n)+・・・+((p−2)n+n)+(pn−2)+((p−1)n−2)+・・・+(n−2)
=2(n+2n+・・・+pn)−(p−1)n−pn−2p+(p−1)n=p(p+1)n−pn−2p
=p2n−2p (個)
ある。
このことから、番号 n−1 のところに穴があく可能性がある。上述と同様に、対称性に注目
すれば、いくつかの場所に絞られる。(これは、あくまでも必要条件!)
十分性を確認するには、その存在を保証する構成法を与えればよい。
(追記) 未菜実さんの質問の核心の部分は次の点である。
n が奇数の場合は、上記で得られた場所すべてに穴があくが、n が偶数の場合は、あく
場合とあかない場合が発生する。穴があく場所を特定するには、どうしたらよいだろうか?
この質問に対して、当HPがいつもお世話になっている「らすかる」さんが、鮮やかな解答
を示してくれた。以下で、そのことをまとめたいと思う。
簡単のために、次の問題で考えることにしよう。
例題 7×7 のマス目に、1×4 のタイルを敷詰める。穴の位置はどこだろうか?

のマス目に、
を埋め込むわけであるが、まず、次のように番号を振ってみる。

上述と同様に対称性に注目すれば、番号3のうち、上図の水色の部分5ヶ所が、穴のあ
く候補となる。
中央の番号3に対しては、
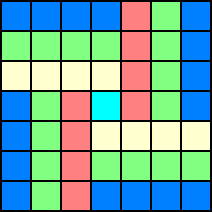
と穴がしっかりあくが、他の番号3の水色の部分については、穴があくとすると不具合が起
こるので、穴があくことはない。
この2つの可能性の判別として、「らすかる」さんは、番号の振り方を変えるという手法で
解決された。
まず、

において、左上部の4×4の正方形の部分に着目すると、他の部分はこの繰り返しとなっ
ている。
さらに、たて横同数の番号が割り振られているので、右下部の配列
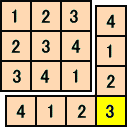
からも分かるように、4×4の正方形の右下部分の番号のみ欠落回数が他の番号よりも
1回分少ない。すなわち、右下部分の番号が他の番号と比べて、1個多いということであ
る。
したがって、4×4の正方形の右下部分の番号の場所で穴があく可能性のあることが
分かる。
番号の振り方を、次のように変えてみる。

先ほどの理論から、4×4の正方形の右下部分の番号3の場所で、穴があく可能性があ
るが、
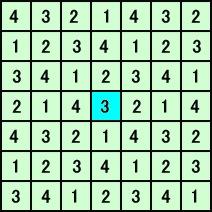
上下、左右の対称性を利用すれば、上図の水色の場所でのみ穴があく可能性があるこ
とが分かり、上述の議論から、これが求める場合である。
(番号の割り振りを変えることにより、可能性がだいぶ狭められる!)
らすかる さんによれば、4×4の正方形の右下部分の番号と同じ番号を他の列に割り
振る方法はいろいろあり、右下部分以外は必ず穴があかないようにできるとのことである。
ただし、n=2 のときは例外で、左上部も穴があくことに注意。
実際に、


であるように、穴があいてしまう。
以上をまとめると、
穴が空く可能性のある場所は、
n>2 のとき、pn行qn列目の場所(p、q は自然数)
である。
逆に、これらの場所に実際に穴があくことは次のようにして分かる。
(らすかる さんによる証明) 左下図は、15×15 (1×4 のタイル)の場合


