質問に対する回答(5) 
平成17年3月2日 当HPの掲示板「出会いの泉」に書き込みのあった質問に対する回
答です。
質問内容 (S さん)
空間に正方形があり、これを一つの平面に正射影すると、2辺の長さが 2 、
、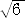 、
、
内角の1つが、30°である平行四辺形になる。
[1] 平行四辺形の2つの対角線の長さを求めよ。
[2] 正方形の面積を求めよ。
(解答)
[1] は、余弦定理を用いて解決される。対角線の長さを K、L とおくと、
K2=(2 )2+(
)2+(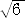 )2−2×2
)2−2×2 ×
×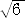 ×cos30°=8+6−12=2
×cos30°=8+6−12=2
L2=(2 )2+(
)2+(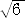 )2−2×2
)2−2×2 ×
×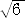 ×cos150°=8+6+12=26
×cos150°=8+6+12=26
よって、 対角線の長さは、  と
と 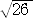
[2] は、2つの可能性が考えられる。
空間にある正方形の最下点が、内角30°の平行四辺形の頂点の直上にある場合と内
角 150°の平行四辺形の頂点の直上にある場合とである。
これらを図示すれば、下図のようになる。(正方形の一辺の長さ : X)
| 図1 |
図2 |
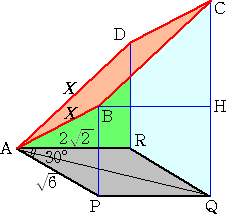 |
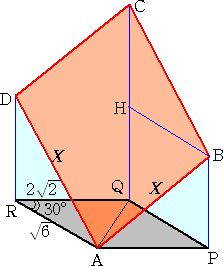 |
図1の場合、BP2=X2−6 、DR2=X2−8 なので、直角三角形AQCにおいて、三平方
の定理を用いれば、
(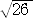 )2+(
)2+(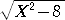 +
+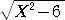 )2=(
)2=( X)2
X)2
ところが、この式を満たす実数Xは存在しないので、図1の場合は起こりえない。
図2の場合、BP2=X2−8 、DR2=X2−6 なので、直角三角形AQCにおいて、三平方
の定理を用いれば、
( )2+(
)2+(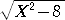 +
+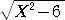 )2=(
)2=( X)2
X)2
これより、 2+X2−8+2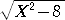
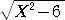 +X2−6=2X2 なので、
+X2−6=2X2 なので、
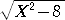
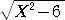 =6
=6
両辺を平方して整理すると、 (X2)2−14X2+12=0
X2≧8 に注意して、 X2=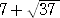
以上から、求める正方形の面積(=X2)は、 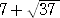 となる。
となる。
(コメント) 書き込みをしていただいた S さん、上記の解答でいかがでしょうか?


