平成16年6月20日、当HPの掲示板「出会いの泉」に、いつもお世話になっている未菜実
さんから質問が寄せられた。
パズルで、川に立ち寄って目的地に行く最短距離を求めるものがありますね。川が直線で
はなくて、曲線(簡単のため円を想定しましたが)の場合はどうやって求めるのか考えたいの
ですが...。
たぶん、次のような問題になると思います。
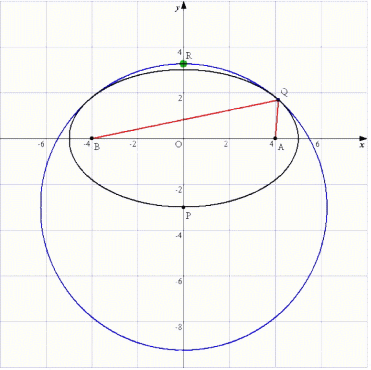
「円Pの内部に点Aと点Bがある。円周上に∠PQA=∠PQBを満足する点Qを作図するには、
どうすればいいか?ただし、∠PQAと∠PQBは重ならないものとする。」
この質問に対して、当HPでは次のように回答した。
円周上に∠PQA=∠PQBを満足する点Qを作図しても、最短距離を求めていることにはな
らないと直感的に思うのですが...?
代数幾何(2次曲線)において、2定点からの距離の和が一定な曲線は、楕円であること
が知られています。したがって、楕円の長径を増大させていって、曲線と最初に交わる点が、
最短距離を与える点だと思います。
これに対して、未菜実さんは、
「物理的に考えると、A点で光を出し、球面鏡で反射させた光をB点で観測すると考えると
その時の光の行路が最短距離になると思ったんですが・・・。
そう仮定すると、反射点では円の接線に関して対象の角度で反射しているはずなので、円
の中心をPとすれば、∠PQA=∠PQB となる。」と説明された。
その後いろいろ検討した結果、次のような場合が考えられるので、当HPの最初の回答
の通りに求めなければならないという結論に至った。