幙栤偵懳偡傞夞摎乮侾俀乯丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂暯惉俀侽擭俀寧俀侾擔丂崅峑俁擭偺庴尡惗偺曽偐傜儊乕儖傪偄偨偩偄偨丅
丂師偺栤戣偵擸傫偱偄傞偲偄偆丅
栤丂戣丂丂倎倶 亖 倢倧倗倎倶丂偺幚悢夝偺屄悢傪媮傔傛丅
丂擸傔傞庴尡惗傪椼傑偡偨傔偵夝偄偰傒偨丅
乮夝乯丂掙偺忦審偐傜丄丂倎亜侽丂乮偨偩偟丄倎亗侾乯偱偁傞丅
丂俀偮偺応崌偵暘偗偰峫偊傞偙偲偵偡傞丅
乮侾乯丂倎亜侾丂偺偲偒丄丂倷 亖 倎倶丂偼壓偵撌丄 倷 亖 倢倧倗倎倶丂偼忋偵撌偺娭悢偱丄偲傕偵憹壛
丂娭悢偱偁傝丄偟偐傕丄捈慄丂倷 亖 倶 偵娭偟偰懳徧偱偁傞丅偙偺偲偒丄俀嬋慄偺岎揰偼昁偢
丂捈慄 倷亖倶丂偺忋偵偁傞偺偱丄
丂倎倶 亖 倢倧倗倎倶丂偺幚悢夝偺屄悢丂偲丂倎倶 亖 倶丂偺幚悢夝偺屄悢丂偼摍偟偄
偲尵偊傞丅
丂傛偭偰丄倎倶 亖 倶丂偺椉曈偺懳悢傪偲偭偰丄丂丂倶丒倢倧倗 倎 亖 倢倧倗 倶 丂偐傜
丂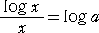
丂偟偨偑偭偰丄嵍曈偺僌儔僼偲塃曈偺僌儔僼偺岎揰偺悢傪挷傋傟偽傛偄丅
丂丂丂丂丂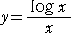 |
丂偺摫娭悢偼丄 |
丂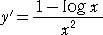 |
丂倷乫亖侽丂傪夝偄偰丄丂倶亖倕丂偲側傞丅
丂侽亙倶亙倕丂偱丄倷 偼扨挷偵憹壛偟丄倶亜倕丂偱扨挷偵尭彮偡傞丅
丂偝傜偵丄
丂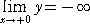 丂丂丂丂丂
丂丂丂丂丂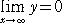
傛偭偰丄
丂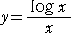
偺僌儔僼偼壓恾偲側傞丅
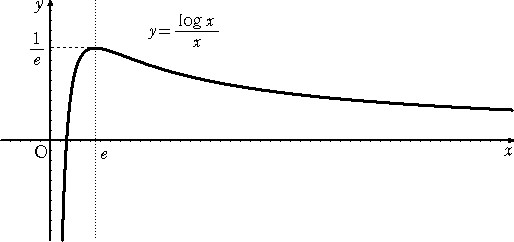
丂偙偺僌儔僼偲丄倶 幉偵暯峴側捈慄 倷 亖 倢倧倗 倎丂乮亜侽乯 偲偺岎揰偺悢傪挷傋傞丅
忋恾傛傝丄
丂侽亙倢倧倗 倎 亙侾/倕丂偡側傢偪丄侾亙倎亙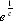 丂偺偲偒丄丂岎揰偼丄俀屄
丂偺偲偒丄丂岎揰偼丄俀屄
丂倢倧倗 倎 亖 侾/倕丂偡側傢偪丄丂倎亖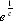 丂偺偲偒丄丂岎揰偼丄侾屄
丂偺偲偒丄丂岎揰偼丄侾屄
丂倢倧倗 倎 亜 侾/倕丂偡側傢偪丄丂倎亜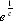 丂偺偲偒丄丂岎揰偼丄侽屄
丂偺偲偒丄丂岎揰偼丄侽屄
乮俀乯丂侽亙倎亙侾丂偺偲偒丄丂倷 亖 倎倶丂偲丂倷 亖 倢倧倗倎倶丂偼偲傕偵壓偵撌偺娭悢偱丄偲傕偵尭彮
丂娭悢偱偁傝丄偟偐傕丄捈慄丂倷 亖 倶 偵娭偟偰懳徧偱偁傞丅偙偺偲偒丄俀嬋慄偺岎揰偼昁偢偟
丂傕捈慄 倷亖倶丂偺忋偩偗偵偁傞偲偼尷傜側偄丅
丂椺偊偽丄倎亖侽丏侽俀丂偺偲偒偼壓恾偺傛偆偵側傝丄岎揰偼 俁屄偁傞丅乮旝柇偱偡偹両乯
丂丂丂丂丂丂丂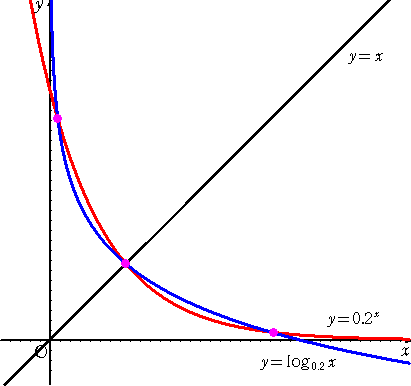
丂倷 亖 倎倶丂偺僌儔僼偲捈慄 倷亖倶 偼昁偢 侾揰偱岎傢傞偺偱丄倷 亖 倎倶丂偲丂倷 亖 倢倧倗倎倶丂偺岎
揰偼彮側偔偲傕 侾屄偼偁傞偙偲偵側傝丄偝傜偵丄僌儔僼偺摿挜偐傜丄岎揰偺悢偼丄侾屄傑偨偼俁
屄偱偁傞丅
丂偄傑丄俀偮偺嬋慄偺岎揰偱丄捈慄 倷亖倶 忋偵側偄揰乮 兛 丆 倎兛 乯偑懚嵼偡傞偨傔偺 倎 偺忦
審傪媮傔偨偄丅偙偺忦審傪枮偨偡偲偒丄俀偮偺嬋慄偺埵抲娭學偼壓恾偲側傞丅
丂丂丂丂丂丂丂丂丂丂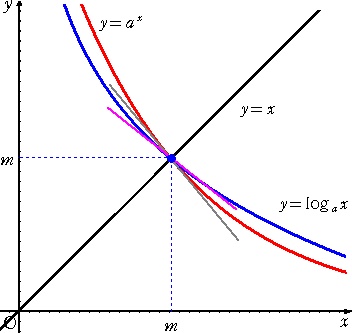
丂捈慄 倷亖倶 忋偺揰乮 倣 丆 倣 乯偵偍偄偰丄俀偮偺嬋慄偼岎傢傞傕偺偲偡傞丅偙偺偲偒丄忦審
傪枮偨偡偨傔偵偼丄揰乮 倣 丆 倣 乯偵偍偗傞俀偮偺嬋慄偺愙慄偺孹偒偵偮偄偰丄
丂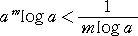
偑惉傝棫偰偽傛偄丅偙偺偲偒丄丂倎倣亖倣丂丄丂倢倧倗 倎亙侽丂偱偁傞偙偲偵拲堄偟偰丄
丂倣丒倢倧倗倎亙亅侾丂偡側傢偪丄丂倢倧倗 倣亙亅侾
丂偙偺偲偒丄丂侽亙倣亙侾/倕丂偲側傞丅
丂偙偙偱丄丂倎倣亖倣丂傛傝丄丂倣丒倢倧倗 倎亖倢倧倗 倣丂偱偁傝丄
丂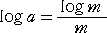
偐傜丄娭悢
丂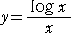
偺僌儔僼傪妶梡偟偰丄丂倢倧倗 倎亙亅倕丂丂偲側傞丅偙偺偲偒丄丂侽亙倎亙倕亅倕丂偑惉傝棫偮丅
傛偭偰丄
丂侽亙 倎 亙倕亅倕丂偺偲偒丄丂岎揰偼丄俁屄
丂倕亅倕亝 倎 亙侾丂偺偲偒丄丂岎揰偼丄侾屄
埲忋偐傜丄媮傔傞幚悢夝偺屄悢偼丄
丂侽亙 倎 亙倕亅倕丂偺偲偒丄俁屄
丂倕亅倕亝 倎 亙侾丂偺偲偒丄侾屄
丂侾亙倎亙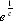 丂偺偲偒丄俀屄
丂偺偲偒丄俀屄
丂倎亖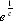 丂偺偲偒丄侾屄
丂偺偲偒丄侾屄
丂倎亜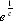 丂偺偲偒丄侽屄
丂偺偲偒丄侽屄
偲側傞丅
乮僐儊儞僩乯丂偙偺栤戣偼丄悢妛嘨傜偟偄栤戣偱偡偹両偱傕丄姰慡夝摎傪彂偔偺偼丄尰栶偺崅
丂丂丂丂丂丂峑惗偵偲偭偰偼擄偟偦偆側丏丏丏梊姶丅
丂暯惉俀侽擭俇寧俀俋擔晅偗偱丄俫俶乽偩傞傑偵偍傫乿偝傫偐傜夝摎偺晄旛偺偛巜揈傪捀偒丄廋
惓偝偣偰偄偨偩偒傑偟偨丅乮忋婰偼廋惓嵪傒乯丅傑偨丄摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞丄傜
偡偐傞偝傫偐傜傕偛嫵帵偄偨偩偒傑偟偨丅偩傞傑偵偍傫偝傫丄傜偡偐傞偝傫偵姶幱偄偨偟傑偡丅