ペントミノの話題　　　　　 　　　　　　　　　　　　　　　　

　ペントミノとは、面積 １ の正方形が５個つながった図形で、下図の ８×８ の正方形から
真ん中の正方形（２×２）を除いて得られる１２種類をいう。

　　　　　　　　　　　

　１２種類それぞれには名前が付けられている。（上記図形で適宜、回転、裏返しを施す。）

Ｐ 型		Ｌ 型		Ｉ 型		Ｎ 型
Ｔ 型		Ｆ 型		Ｕ 型		Ｖ 型
Ｗ 型		Ｘ 型		Ｙ 型		Ｚ 型

　平成１７年３月２９日に当ＨＰの掲示板「出会いの泉」に、いつもお世話になっている未菜
実さんから、Ｘ 型のペントミノに関して面白い問題の提起があった。

問　題

　ｎ×ｎ （ｎ≧３）のマス目に、ｘ-ペントミノが一つも置けなくなるように穴（１×１）を配置する
とき、穴の最小数を求めよ。

とのことである。問題は、ｎ＝９　以降について、その規則性はどうなっているだろうか？と
いう疑問である。

　この提起された問題について、当ＨＰがいつもお世話になっている「らすかる」さんがプロ
グラムを実際に組んで、以下のような解を列挙された。（当ＨＰの掲示板より転載）

　掲示板は、時間の経過とともに消え去る運命なので、ここに、未菜実さんとらすかるさん
の研究の成果を書き留めることにした。（未菜実さんとらすかるさんに感謝いたします。）

　以下は、全て最小の解の一つである。

ｎ＝３　のとき、穴の最小数は、　１		ｎ＝４　のとき、穴の最小数は、　２
ｎ＝５　のとき、穴の最小数は、　３		ｎ＝６　のとき、穴の最小数は、　４
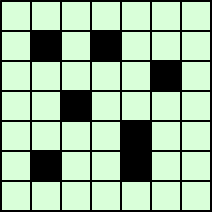
ｎ＝７　のとき、穴の最小数は、　７		ｎ＝８　のとき、穴の最小数は、　１０
ｎ＝９　のとき、穴の最小数は、　１２		ｎ＝１０　のとき、穴の最小数は、　１６
ｎ＝１１　のとき、穴の最小数は、　２０		ｎ＝１２　のとき、穴の最小数は、　２４
ｎ＝１３　のとき、穴の最小数は、　２９		ｎ＝１４　のとき、穴の最小数は、　３５
ｎ＝１５　のとき、穴の最小数は、　４０
ｎ＝１６　のとき、穴の最小数は、　４７

　らすかるさんによれば、ｎ＝１５ の場合に２時間かかったのを１８分で終わるところまで
プログラムを高速化し、ｎ＝１６ の場合を１３時間かけて求められたそうです。私の知らな
い世界で事が運んでいるようで、らすかる様とその愛用のパソコン殿に「お疲れ様！」と
コメントするしかないですね。（ｎ＝１７ の場合は１ヶ月くらいかかるとのことです．．．！！）


　らすかるさんからの続報です。（平成２４年４月１９日付け・・・７年ぶり！）

　私が、２００５年にプログラムを作って計算して、n=16までの結果をオンライン整数列大辞
典の「A104519」に新規登録しましたが、久しぶりに見たら、n=29まで拡張されていました。
（私が計算した部分が正しかったことも証明されたことになりますね。）

　そこにURLが載っている論文のPDFを見ると、図も掲載されています。
（最外周を除いた図になっています）　すごいですね〜！

（コメント）　確かに感動的！ですね。しかも、アルゴリズムまで．．．。