
1.2項分布
確率変数Xの確率分布が2項分布であるとは、Xが次のような分布に従うときを言う。
Xの取り得る値 0、1、2、・・・、n に対して、X=k に対する確率が
P(X=k)=nCkpk(1−p)n-k (0<p<1)
このとき、Xは「2項分布B(n,p)に従う」と言う。
(注意) 定義から分かるように、反復試行の確率分布は、2項分布である。
また、 Σk=0〜n nCkpk(1−p)n-k=(p+1−p)=1 である。
(問) 1枚の硬貨を3回続けて投げるとき、表の出る回数をXとする。Xの確率分布を求め、
E(X)、V(X)、σ(X)を求めよ。
2項分布B(n,p)の期待値、分散については、次の公式が重要である。
E(X)=np 、V(X)=npq (ただし、q=1−p)
(問) 上の公式の証明を与えよ。
(Hint) (px+q)n=Σk=0〜n nCkpkqn-k・xk の両辺をxについて微分せよ。
(問) 1個のさいころを720回振るとき、1の目の出る回数をXとする。Xの期待値、分散、
標準偏差を求めよ。
2.正規分布
2項分布のように、確率変数Xの値が飛び飛びの値をとり、それらに対応する確率の値が
階段関数になるとき、Xを離散的な確率変数という。これに対して、確率変数Xの値が連続
的な値をとる場合がある。
確率変数Xの取り得る値が区間[α,β]で、確率P(a≦X≦b)が、
P(a≦X≦b)=∫abF(x)dx ただし、F(x)≧0 で、∫αβF(x)dx=1
で与えられるとき、Xのことを連続的な確率変数といい、F(x)のことを確率密度関数という。
(問) Xが連続的な確率変数で、その確率密度関数F(x)が、F(x)=kx (0≦x≦2) と与
えられているとき、次の問いに答えよ。
(1) kの値を求めよ。 (2) P(1≦X≦3/2)を求めよ。
連続的な確率変数Xが正規分布とは、確率密度関数F(x)が、
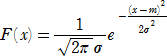
で与えられるときをいう。このとき、Xは正規分布N(m,σ2)に従うという。
連続的な確率変数Xに対して、
m=E(X)=∫αβx・F(x)dx 、 V(X)=∫αβ(x−m)2・F(x)dx
と定義する。
(問) [0,6]で定義された連続的な確率変数Xがある。Xの確率密度関数を、F(x)=ax
とするとき、平均、分散、標準偏差を求めよ。
3,標準正規分布とその応用
正規分布の確率密度関数F(x)について、次の事柄が成り立つ。
(1) y=F(x)のグラフ(正規分布曲線) ・・・ x=mに関して線対称
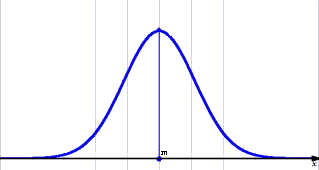
(2) ∫-∞∞F(x)dx=1 (面積が1) (→ 参考:「無限の拡がりを持つ面積1の図形」)
(3) E(X)=m 、 V(X)=σ2 、σ(X)=σ
(4) P(m−σ≦X≦m+σ)=0.683 、P(m−2σ≦X≦m+2σ)=0.954
P(m−3σ≦X≦m+3σ)=0.997
平均が0、分散が1の正規分布を標準正規分布N(0,1)という。
通常、P(u)=P(0≦X≦u) と表す。
(問) 正規分布表を用いて、P(1.2)、P(2.3)の値を求めよ。
(問) 次の確率を求めよ。
(1) P(1≦X≦2.5) (2) P(−1≦X≦2) (3) P(X≧1)
正規分布N(m,σ2)は、標準化 (X−m)/σ=Z を施せば、標準正規分布N(0,1)に
なる。
(問) XがN(2,25)に従うとき、P(2≦X≦4)を求めよ。
(問) XがN(4,9)に従うとき、P(7≦X≦10)を求めよ。
正規分布の応用を考えてみよう。
(問) ある高校の3年生300人について、200点満点の実力テストを行った結果、平均点
は、169.4点、標準偏差5点の正規分布にだいたい従う分布が得られた。
このとき、次の問いに答えよ。
(1) 170点〜180点の生徒は何人いるか。
(2) 160点とった生徒は、何番位か。
(3) 上位50名の中に入るには、何点以上あればよいか。
(問) センター試験地理の受験者は10万人で、平均点が48点、標準偏差が14点の正規
分布になるという大学入試センターの発表があった。次のものを求めよ。
(1) 90点とった人は、何番位か。
(2) 上位1万名中に入るためには、何点以上あればよいか。
(追記) 令和4年7月29日付け
当HP読者のHN「0hyose」さんよりご投稿いただいた。(令和4年7月27日付け)
テストを受けた全体の人数が500人で、400位以下が補習です。何点以下が補習でしょう
か?ただし、正規分布に従い、標準偏差9点、平均48点とする。
ちなみに、先生は、400÷500=0.8→0.2(20%) ここで急に -0.84 が出てきて、
48+9×(-0.84)=40.44 としていました。
どのように -0.84 を出すのですか?よろしくお願いします。
(コメント) 400÷500=0.8 なので、 P(α≦X)≒0.8 すなわち、 P(X≦α)≒0.2
となる近似値を標準正規分布表で探すと、標準偏差をσとして、
P(X≦α)=P(0.84σ)=0.200454 である。
すなわち、平均から 0.84σ だけ小さいところが、400位(下位20%)の点数となる。
よって、400位の点数は、48-0.84*9=40.44(点) となる。
以上から、点数に端数はないと思われるので、40点以下が補習対象となる。
4.ラプラスの中心極限定理
確率変数Xが2項分布B(n,p)に従うとする。n が十分大きいとき、Xは正規分布
N(np,npq)に従うものと見なせる。(中心極限定理・・・2項分布の正規近似)
(注意) 経験によれば、
p≦1/2 のとき、 n>5/p p≧1/2 のとき、 n>5/(1−p)
であるような n であれば、正規近似は実用上十分であることが分かっている。
Xは離散的な変数だから、Xは飛び飛びの値しかとらない。ところで、2項分布を正規分布
と見なすということは、Xを連続的な変数と見なすことである。
よって、P(a≦X≦b)を計算するとき、四捨五入して「a≦X≦b」となると考えて(←大切)、
a−0.5≦X<b+0.5 の確率を計算しなければならない。このような計算を半整数補正
という。
(問) さいころを720回投げて、1の目が出る回数をXとする。Xが100以下の値をとる確率
を求めよ。
(問) さいころを720回投げたとき、1の目が120回以上または80回以下出る確率を求め
よ。
(問) 数学の問題を5題中4題は解けると言われているS君が100題の問題を解くことに
なった。次の問いに答えよ。
(1) 90題以上を解くことができる確率を求めよ。
(2) 80%以上の確率で解くことが出来る問題数の最大値を求めよ。