無限の拡がりをもつ面積１の図形　　　　　　　　　　　　　　

　面積を持つなら、その図形には限りがある（数学的には有界）と、高校生の頃まで、ずっと
思っていた。大学に入って重積分とか正規分布の確率密度関数などを知るようになって、そ
の考えは根底から覆された。正方形の内部の点を全て通るというペア曲線に匹敵するぐら
いの衝撃を受けたことを今でも覚えている。



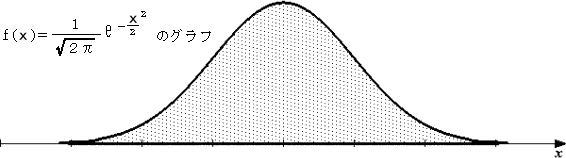
　この関数 ｆ（ｘ）に対して面積を求めると、　∫_-∞^∞ ｆ（ｘ）ｄｘ＝１　となる。

　実際に、　Ｉ＝∫_-∞^∞ ｅ^-x2ｄｘ　とおくと、対称性から、　Ｉ/２＝∫₀^∞ ｅ^-x2ｄｘ

　このとき、　∫₀^∞ ｅ^-x2ｄｘ∫₀^∞ ｅ^-ｙ2ｄｙ＝∫₀^∞∫₀^∞ ｅ^-x2-ｙ2ｄｘｄｙ

　ここで、　ｘ＝ｒ・ｃｏｓθ、ｙ＝ｒ・ｓｉｎθ　と変数変換して定積分を求めると、

　　上式＝∫₀^∞ ｒｅ^-ｒ2ｄｒ∫₀^π/2 ｄθ＝π/４

　よって、　Ｉ/２＝√π/２　より、　Ｉ＝√π　となる。

　このことを利用して、　ｘ＝ｔ　と変数変換して定積分を求めると、

　　　∫_-∞^∞ ｆ（ｘ）ｄｘ＝Ｉ/√π＝１

が成り立つ。

（参考文献：　一松　信　著　解析学序説　下巻（裳華房））