点予想問題 
直線は2点で決まることを考えると、全ての直線上に少なくとも2つの点があるような点の配
置(ドットダイアグラムという)を考えることは容易であるし、また、任意の点の配置はこの条件
を満たしている。以下において、考える点の集合は有限集合とする。
ところが、全ての点が1直線上にある場合を除くと、
全ての直線上に少なくとも3つの点があるような点の配置を作る
ということは容易ではない。
その結果、そのような配置はないだろうというのが、点予想問題といわれているものである。
この問題は、何十年もの間未解決で、多くの数学者たちが挑戦し、敗れ去っていったと聞く。
しかし、その証明は、何ら難しい数学的知識を必要とはしなかった。
今、全ての直線上に少なくとも3つの点があるような点の配置が存在したとする。その任意の
2点を結ぶ直線を全て考える。点の個数は有限個なので、直線の数も有限個である。
(n個の点があるとき、直線の個数は、高々n(n−1)/2 個である。)
そこで、全ての点と全ての直線との距離を考えると、その距離全体の個数も有限個である。
よって、その中に最小値が存在する。
最小値を与える点をAとし、直線をL、直線上の2つの点をB、Cとする。
点Aから直線Lに下ろした垂線の足をHとすると、Hは線分BC上にあるとしてよい。
実際に、Hで分割された半直線のどちらか一方に、2点B、Cがあると仮定する。一般性を
失うことなく、B、C、Hの順に並んでいるとしてよい。C=Hであってもよい。このとき、
CからABまでの距離≦HからABまでの距離<AH
となって、AHが最小であることに反する。
よって、Hに関して、2点B、Cは反対側にある。さらに、仮定から、直線L上には第3の点
(PまたはQ)が存在する。第3の点は、一般性を失うことなく、
P、B の順 または B、Q の順
としてよい。このとき、上記と同様の理由から、
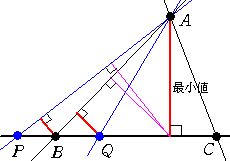 |
PまたはQの何れの場合も、Aと直線Lとの距離が
最短であることに矛盾する。
従って、全ての直線上に少なくとも3つの点がある
ような点の配置を考えることは、不可能である。
(平成23年8月23日付けで証明を修正)
|
(参考文献:サイモン・シン著 青木 薫 訳 フェルマーの最終定理 (新潮社))
余談になるが、訳者の青木 薫さんは、私と同じ高校の同級生である。一緒に電車通学し
ていた頃が懐かしい...。そういえば、模擬試験の問題を貸しっぱなしじゃなかったっけ?
(追記) 平成22年12月4日付け
当HPの掲示板「出会いの泉」に、HN「うなー」さんが次のような書き込みをされた。
先ほどフェルマーの最終定理を読み終わりました。その中に出てきた点予想について、補
遺を読んだのですが理解できませんでした。「線と点の距離で最小値」という所で、なぜ最小
値なのかという疑問が解決しなくて進めずにいます。
「うなー」さんの疑問に触発されて、上図をもっと分かりやすいものに修正した。この図を見
て「うなー」さんの疑問が解決することを祈ります。
上記の証明について、HN「数学素人」さんからの質問です。(平成23年8月22日付け)
私も、「うなー」さんとほぼ同様に、なぜ点Aが最小値になるか理解できません。また、点P、
Qが点Aより短いことが理解でき、仮定がまちがいなのも理解できるのですが、それが「全て
の直線上に少なくとも3つの点があるような点の配置を考えることは不可能である」にはつ
ながりません。
詳しく教えていただけるか、詳しく説明された本(フェルマーの最終定理以外)やHPをご紹
介いただけると助かります。気になって、気になってしょうがありません。
FNさんにご回答いただきました。(平成23年8月22日付け)
確かに、「点予想問題」のところの証明は不十分ですね。証明において本質的なのは次の
ことです。
Hを、AからLに引いた垂線の足とする。LをHによって、2つの部分に分けたとき、その一方
に2点がある。
L上に3点があるからこれは成り立ちます。これを明言すべきです。B、CがHに関して同じ
側にあるとしてよいから、B、C、Hの順に並んでいるとしてよい。C=Hであってもよい。この
とき、CからABまでの距離≦HからABまでの距離<AHとなって、AHが最小であることに反す
る。
さらに、FNさんからの回答の続きです。(平成23年8月22日付け)
疑問点はちょっと違う所にあるのかもしれないような気がしてきました。つけたします。その
ためにまず問題を正確に表現します。
平面上の有限個の点からなる集合Sで、次の条件を満たすものは存在しない。
(1) Sは同一直線上にない3点を含む。
(2) Sの異なる任意の2点A、Bに対して、直線AB上に、A、B以外のSの点Cが存在する。
有限集合というのが本質的で、無限集合なら当然存在します。平面上の点全部とか格子
点全部とかいくらでもあります。
同一直線上にない3点A、B、Cに対して、点Aと直線BCの距離を、d(A,BC) と書く。前に
書いたことから、(あるいは同様にして)次のことが成り立ちます。
同一直線上にないSの3点 A、B、C に対して、Sの3点 A'、B'、C' で、
d(A',B'C')<d(A,BC) を満たすものが存在する。
この操作は無限に繰り返すことができることになるが、有限集合だから、不可能である。
いわゆる無限降下法です。こういう証明でもいいのですが、有限集合だから、d(A,BC)に
最小値が存在するとして矛盾を導くという書き方をすることも多いです。その方が綺麗とい
う感じがあります。
数学素人さんの疑問「なぜ、点Aが最小値になるか理解できません。」ですが、最小にな
る点をAと置いたということです。
(コメント) FNさん、証明の不備のご指摘、ありがとうございます。再度証明を読み返して
みて、誤解が生じそうな部分を修正しました。
(追記) 平成23年5月11日付け
平面上の点の配置に関連して、次のような問題が知られている。
平面上に、n×n 個の点が格子状に配置され、その中から次の条件:
2n 個の点のうち、どの3点を選んでも同一直線上にはない
を満たすような 2n 個の点を選ぶことができるだろうか。
この問題は、「No-Three-in-Line 問題」と言われ、
「十分大きな n については、条件を満たすような点は選べないだろう」
という予想があるらしいが、n=17 までは解が見つかっている。
具体的な点の配置例を探訪してみよう。
n=2 のとき、
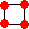
n=3 のとき、
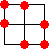
n=4 のとき、
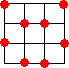
何とはなしに、塾生のOさんにこの問題を出題したら、瞬時に
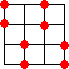
という解を見つけてくれた!(平成23年5月18日付け)
異なる解は何通り?という問いが自然に芽生えてきます...。
n=4 の場合、他の解は、
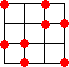
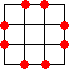
である。
オンライン整数列大辞典によれば、対称なもの、回転して重なるものを同一視して、
| |
| n の値 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
・・・ |
| 解の個数 |
0 |
1 |
1 |
4 |
5 |
11 |
22 |
57 |
51 |
・・・ |
|
が知られているようだ。
n=5 のとき、
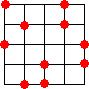
塾生のOさんは、さらに次の解も見いだされた!(平成23年5月19日付け)
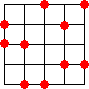
n=6 のとき、
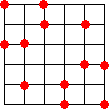
塾生のOさんは、さらに次の解も見いだされた!(平成23年5月19日付け)
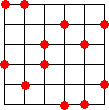
(コメント) 直線の傾きが、 0、±1、±2、±1/2、±3、±1/3、・・・、∞ である場合に、
その上に3点がないかどうかのチェックが大変ですね!n=5 から
n=6 になった
だけで、難しさは想像以上にアップしています...。そんな中、Oさんの解決力は
素晴らしいですね。
当HPがいつもお世話になっているHN「GAI」さんが n=26 のときの解を見出されました。
(平成23年5月19日付け)
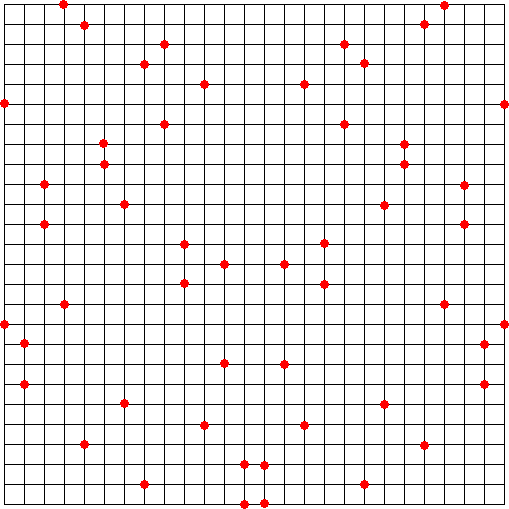
(コメント) GAIさんに感謝します。何やら左右対称ですね!作り方のコツですか?
平成23年現在、知られている最大の n の値は、「52」(Flammenkamp)らしい。
n≦46、n=48、n=50、n=52について、少なくとも一つの解が知られている。
at さんより、次のサイトをご紹介いただいた。(平成23年5月21日付け)
http://wwwhomes.uni-bielefeld.de/achim/no3in/readme.html
また、サイト「no-three-in-line問題」においては、画面上で点の配置を決め、正しいか正し
くないか判定してくれるので重宝している。皆さんも、遊んでみてはいかがですか?
GAI さんが、「対称性が強いパターン」と題して、n=2 から n=8 までの解について調べ
られた。(平成23年5月23日付け)
n=2 のとき、
● ●
● ●
n=3 のとき、
● ● ・
● ・ ●
・ ● ●
n=4 のとき、
● ● ・ ・
・ ・ ● ●
● ● ・ ・
・ ・ ● ●
● ・ ● ・
・ ● ・ ●
・ ● ・ ●
● ・ ● ・
● ・ ● ・
・ ・ ● ●
● ● ・ ・
・ ● ・ ●
・ ● ● ・
● ・ ・ ●
● ・ ・ ●
・ ● ● ・
n=5 のとき、
● ● ・ ・ ・
● ・ ・ ● ・
・ ・ ・ ● ●
・ ● ● ・ ・
・ ・ ● ・ ●
n=6 のとき
● ● ・ ・ ・ ・ : ・ ● ● ・ ・ ・
・ ・ ・ ● ・ ● : ・ ・ ● ・ ・ ●
・ ● ・ ・ ● ・ : ・ ・ ・ ・ ● ●
● ・ ● ・ ・ ・ : ● ● ・ ・ ・ ・
・ ・ ・ ・ ● ● : ● ・ ・ ● ・ ・
・ ・ ● ● ・ ・ : ・ ・ ・ ● ● ・
:
● ・ ● ・ ・ ・ : ・ ● ● ・ ・ ・
・ ・ ● ・ ● ・ : ・ ・ ・ ・ ● ●
● ● ・ ・ ・ ・ : ● ・ ● ・ ・ ・
・ ・ ・ ・ ● ● : ・ ・ ・ ● ・ ●
・ ● ・ ● ・ ・ : ● ● ・ ・ ・ ・
・ ・ ・ ● ・ ● : ・ ・ ・ ● ● ・
:
・ ● ● ・ ・ ・ : ・ ● ・ ● ・ ・
● ・ ・ ・ ● ・ : ・ ・ ● ・ ・ ●
● ・ ● ・ ・ ・ : ● ・ ・ ・ ● ・
・ ・ ・ ● ・ ● : ・ ● ・ ・ ・ ●
・ ● ・ ・ ・ ● : ● ・ ・ ● ・ ・
・ ・ ・ ● ● ・ : ・ ・ ● ・ ● ・
:
・ ● ● ・ ・ ・ : ・ ● ・ ● ・ ・
・ ・ ● ・ ● ・ : ・ ・ ・ ● ・ ●
● ・ ・ ・ ・ ● : ● ● ・ ・ ・ ・
● ・ ・ ・ ・ ● : ・ ・ ・ ・ ● ●
・ ● ・ ● ・ ・ : ● ・ ● ・ ・ ・
・ ・ ・ ● ● ・ : ・ ・ ● ・ ● ・
n=7 のとき
● ・ ● ・ ・ ・ ・ : ・ ● ・ ・ ● ・ ・
・ ・ ・ ・ ● ● ・ : ・ ● ・ ・ ● ・ ・
・ ● ・ ● ・ ・ ・ : ● ・ ・ ● ・ ・ ・
● ・ ・ ・ ・ ・ ● : ● ・ ・ ・ ・ ・ ●
・ ・ ・ ● ・ ● ・ : ・ ・ ・ ● ・ ・ ●
・ ● ● ・ ・ ・ ・ : ・ ・ ● ・ ・ ● ・
・ ・ ・ ・ ● ・ ● : ・ ・ ● ・ ・ ● ・
:
● ・ ・ ● ・ ・ ・ : ・ ● ・ ・ ● ・ ・
・ ・ ● ・ ・ ● ・ : ・ ● ・ ・ ● ・ ・
・ ・ ・ ・ ・ ● ● : ・ ・ ・ ● ・ ・ ●
・ ・ ● ・ ● ・ ・ : ● ・ ・ ・ ・ ・ ●
● ● ・ ・ ・ ・ ・ : ● ・ ・ ● ・ ・ ・
・ ● ・ ・ ● ・ ・ : ・ ・ ● ・ ・ ● ・
・ ・ ・ ● ・ ・ ● : ・ ・ ● ・ ・ ● ・
:
・ ● ・ ● ・ ・ ・ : ・ ● ・ ・ ● ・ ・
● ・ ・ ・ ・ ・ ● : ・ ・ ・ ● ● ・ ・
・ ・ ● ・ ● ・ ・ : ● ● ・ ・ ・ ・ ・
・ ● ・ ・ ・ ● ・ : ● ・ ・ ・ ・ ・ ●
・ ・ ● ・ ● ・ ・ : ・ ・ ・ ・ ・ ● ●
● ・ ・ ・ ・ ・ ● : ・ ・ ● ● ・ ・ ・
・ ・ ・ ● ・ ● ・ : ・ ・ ● ・ ・ ● ・
:
・ ● ・ ● ・ ・ ・ : ・ ● ・ ・ ● ・ ・
・ ・ ● ・ ● ・ ・ : ・ ・ ・ ・ ● ● ・
● ・ ・ ・ ・ ・ ● : ● ・ ・ ● ・ ・ ・
・ ● ・ ・ ・ ● ・ : ● ・ ・ ・ ・ ・ ●
● ・ ・ ・ ・ ・ ● : ・ ・ ・ ● ・ ・ ●
・ ・ ● ・ ● ・ ・ : ・ ● ● ・ ・ ・ ・
・ ・ ・ ● ・ ● ・ : ・ ・ ● ・ ・ ● ・
:
・ ● ・ ● ・ ・ ・ : ・ ● ・ ・ ・ ● ・
・ ・ ・ ・ ● ・ ● : ・ ・ ● ● ・ ・ ・
● ・ ● ・ ・ ・ ・ : ● ・ ● ・ ・ ・ ・
・ ● ・ ・ ・ ● ・ : ● ・ ・ ・ ・ ・ ●
・ ・ ・ ・ ● ・ ● : ・ ・ ・ ・ ● ・ ●
● ・ ● ・ ・ ・ ・ : ・ ・ ・ ● ● ・ ・
・ ・ ・ ● ・ ● ・ : ・ ● ・ ・ ・ ● ・
n=8 のとき、
● ・ ● ・ ・ ・ ・ ・ : ・ ・ ● ● ・ ・ ・ ・
・ ・ ・ ● ・ ● ・ ・ : ・ ・ ● ● ・ ・ ・ ・
・ ● ・ ● ・ ・ ・ ・ : ・ ・ ・ ・ ・ ・ ● ●
● ・ ・ ・ ・ ・ ● ・ : ・ ・ ・ ・ ・ ・ ● ●
・ ● ・ ・ ・ ・ ・ ● : ● ● ・ ・ ・ ・ ・ ・
・ ・ ・ ・ ● ・ ● ・ : ● ● ・ ・ ・ ・ ・ ・
・ ・ ● ・ ● ・ ・ ・ : ・ ・ ・ ・ ● ● ・ ・
・ ・ ・ ・ ・ ● ・ ● : ・ ・ ・ ・ ● ● ・ ・
:
・ ● ● ・ ・ ・ ・ ・ : ・ ・ ● ・ ● ・ ・ ・
● ・ ・ ・ ● ・ ・ ・ : ・ ● ・ ● ・ ・ ・ ・
・ ・ ● ・ ● ・ ・ ・ : ・ ● ・ ・ ・ ・ ・ ●
・ ・ ・ ・ ・ ・ ● ● : ● ・ ● ・ ・ ・ ・ ・
● ● ・ ・ ・ ・ ・ ・ : ・ ・ ・ ・ ・ ● ・ ●
・ ・ ・ ● ・ ● ・ ・ : ● ・ ・ ・ ・ ・ ● ・
・ ・ ・ ● ・ ・ ・ ● : ・ ・ ・ ・ ● ・ ● ・
・ ・ ・ ・ ・ ● ● ・ : ・ ・ ・ ● ・ ● ・ ・
:
・ ● ・ ● ・ ・ ・ ・ : ・ ・ ● ・ ● ・ ・ ・
・ ・ ● ・ ● ・ ・ ・ : ・ ● ・ ・ ・ ● ・ ・
● ・ ・ ・ ・ ・ ● ・ : ・ ・ ・ ・ ● ・ ・ ●
・ ・ ・ ・ ・ ● ・ ● : ● ・ ・ ・ ・ ・ ● ・
● ・ ● ・ ・ ・ ・ ・ : ・ ● ・ ・ ・ ・ ・ ●
・ ● ・ ・ ・ ・ ・ ● : ● ・ ・ ● ・ ・ ・ ・
・ ・ ・ ● ・ ● ・ ・ : ・ ・ ● ・ ・ ・ ● ・
・ ・ ・ ・ ● ・ ● ・ : ・ ・ ・ ● ・ ● ・ ・
:
・ ● ・ ● ・ ・ ・ ・ : ・ ・ ● ・ ● ・ ・ ・
・ ・ ・ ・ ● ・ ● ・ : ・ ・ ● ● ・ ・ ・ ・
● ・ ● ・ ・ ・ ・ ・ : ・ ・ ・ ・ ・ ・ ● ●
・ ・ ・ ・ ・ ● ・ ● : ● ・ ・ ・ ・ ・ ● ・
● ・ ● ・ ・ ・ ・ ・ : ・ ● ・ ・ ・ ・ ・ ●
・ ・ ・ ・ ・ ● ・ ● : ● ● ・ ・ ・ ・ ・ ・
・ ● ・ ● ・ ・ ・ ・ : ・ ・ ・ ・ ● ● ・ ・
・ ・ ・ ・ ● ・ ● ・ : ・ ・ ・ ● ・ ● ・ ・
:
・ ● ・ ● ・ ・ ・ ・ : ・ ・ ● ・ ● ・ ・ ・
・ ・ ・ ・ ・ ● ・ ● : ・ ・ ・ ● ・ ● ・ ・
・ ・ ● ・ ● ・ ・ ・ : ・ ● ・ ・ ・ ・ ・ ●
● ・ ・ ・ ・ ・ ● ・ : ● ・ ・ ・ ・ ・ ● ・
● ・ ・ ・ ・ ・ ● ・ : ・ ● ・ ・ ・ ・ ・ ●
・ ・ ● ・ ● ・ ・ ・ : ● ・ ・ ・ ・ ・ ● ・
・ ・ ・ ・ ・ ● ・ ● : ・ ・ ● ・ ● ・ ・ ・
・ ● ・ ● ・ ・ ・ ・ : ・ ・ ・ ● ・ ● ・ ・
:
・ ● ・ ・ ● ・ ・ ・ : ・ ・ ● ・ ● ・ ・ ・
・ ・ ・ ● ・ ● ・ ・ : ・ ・ ・ ・ ● ● ・ ・
・ ● ・ ・ ・ ・ ・ ● : ・ ● ・ ・ ・ ・ ・ ●
● ・ ・ ・ ・ ● ・ ・ : ● ● ・ ・ ・ ・ ・ ・
・ ・ ● ・ ・ ・ ・ ● : ・ ・ ・ ・ ・ ・ ● ●
● ・ ・ ・ ・ ・ ● ・ : ● ・ ・ ・ ・ ・ ● ・
・ ・ ● ・ ● ・ ・ ・ : ・ ・ ● ● ・ ・ ・ ・
・ ・ ・ ● ・ ・ ● ・ : ・ ・ ・ ● ・ ● ・ ・
以下、工事中










