放物線の作図　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　下図は、曲線群 Ｆ＝｛ ｙ＝ｍｘ＋ｍ²　（ ｍ は実数） ｝をパソコンで描いたものである。


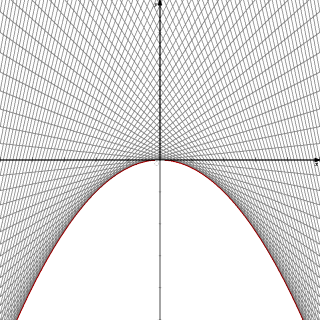
　 　それらに接する包絡線として、放物線　ｙ＝−（1/4）ｘ²　の姿
　　が垣間見える。


　　　このページでは、パソコンに頼らず手書きで放物線を描くこと
　　を試みたいと思う。



　作図のために、次の美しい放物線の性質が用いられる。


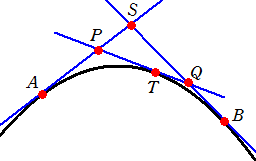
　　　放物線に対して、３本の接線を引いたとき、

　　　　　ＳＰ/ＰＡ＝ＢＱ/ＱＳ＝ＱＴ/ＴＰ

　　が成り立つ。





（証明）　簡単のため、放物線を ｙ＝ａｘ² とし、接点の座標を、

　　　　　　　　Ａ（α，ａα²）、Ｂ（β，ａβ²）、Ｔ（γ，ａγ²）

とすると、Ｓ（（α＋β）/２，ａαβ）、Ｐ（（α＋γ）/２，ａαγ）、Ｑ（（γ＋β）/２，ａγβ）

　このとき、　ＳＰ²＝（β−γ）²/４＋ａ²α²（β−γ）²＝（１＋４ａ²α²）（β−γ）²/４

　　　　　　　　ＰＡ²＝（γ−α）²/４＋ａ²α²（γ−α）²＝（１＋４ａ²α²）（γ−α）²/４

　　　より、　ＳＰ²/ＰＡ²＝（β−γ）²/（γ−α）²　が成り立つ。

　同様にして、　ＢＱ²＝（β−γ）²/４＋ａ²β²（β−γ）²＝（１＋４ａ²β²）（β−γ）²/４

　　　　　　　　　ＱＳ²＝（γ−α）²/４＋ａ²β²（γ−α）²＝（１＋４ａ²β²）（γ−α）²/４

　　　より、　ＢＱ²/ＱＳ²＝（β−γ）²/（γ−α）²　が成り立つ。

　また、　ＱＴ²＝（β−γ）²/４＋ａ²γ²（β−γ）²＝（１＋４ａ²γ²）（β−γ）²/４

　　　　　ＴＰ²＝（γ−α）²/４＋ａ²γ²（γ−α）²＝（１＋４ａ²γ²）（γ−α）²/４

　　　より、　ＱＴ²/ＴＰ²＝（β−γ）²/（γ−α）²　が成り立つ。

　以上から、　ＳＰ²/ＰＡ²＝ＢＱ²/ＱＳ²＝ＱＴ²/ＴＰ²　すなわち、

　　　　ＳＰ/ＰＡ＝ＢＱ/ＱＳ＝ＱＴ/ＴＰ

が成り立つ。　　（証終）


（コメント）　もっと純粋に幾何的な解法を追究しようとしたが思いつかず、結局解析的な解答
　　　　　　に落ち着いてしまった。比の値が、放物線に依らずに一定になることが面白い。果
　　　　　　たして、もっとエレガントな解法は存在するのだろうか？


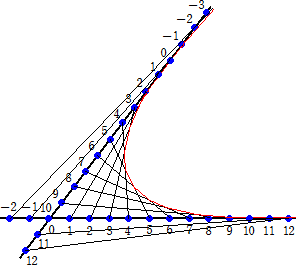
　上記で得られた性質から放物線が得られる。

　交わる２直線上に等分点を左図のように設
け、番号を付ける。同番号同士を線分で結ぶ
と、それらは放物線の接線となっている。










　放物線の性質って、意外と知らないものが多いことに気づかされる。次の美しい放物線の
性質に出会い、何となく得した気分で心地よい。


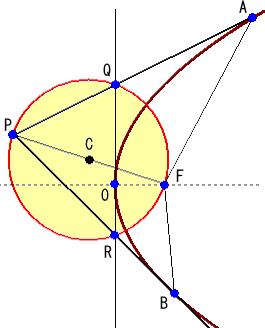
　　（１）　焦点Ｆの放物線において、放物線外の点
　　　　をＰとし、Ｐより放物線に接線ＰＡ、ＰＢを引く。

　　　　　このとき、△ＡＰＦ∽△ＰＢＦが成り立つ。

　　（２）　焦点Ｆの放物線において、放物線外の点
　　　　をＰとし、ＰＦを直径とする円Ｃを描く。

　　　　　　この円Ｃが、放物線の頂点Ｏを通り軸に
　　　　垂直な線分と交わる点をＱ、Ｒとする。

　　　　　このとき、ＰＱ、ＰＲは放物線の接線となる。






（証明）　（１）　放物線の準線上に、Ａ、Ｂより垂線の足Ｄ、Ｅを下ろす。さらに、線分ＡＰとＦＤ
　　　　　　　　の交点をＭ、線分ＡＰと準線の交点をＮとおく。

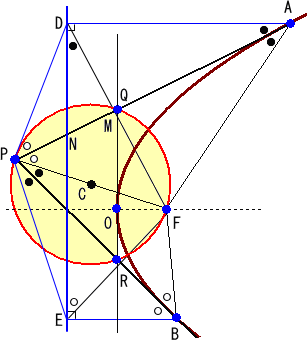このとき、放物線の性質から、 　∠ＦＡＭ＝∠ＤＡＭで、ＡＦ＝ＡＤ、ＡＭ共通 　より、　△ＡＦＭ≡△ＡＤＭ　が成り立つ。 よって、　ＦＭ＝ＤＭ　、ＡＰ⊥ＦＤ 　このとき、△ＡＤＮ∽△ＤＭＮ　より、 　　　∠ＦＡＰ＝∠ＤＡＰ＝∠ＥＤＦ　・・・（*） ＰＤ＝ＰＥ＝ＰＦ　より、３点Ｄ、Ｅ、ＦはＰを中 心とする同一円周上にあるので、 　　　∠ＡＰＦ＝∠ＤＥＦ　・・・（**） 　よって、（*）（**）より、２角相等なので、 　　　△ＡＰＦ∽△ＤＥＦ 　同様にして、　△ＤＥＦ∽△ＰＢＦ　が成り 立つので、 　　　　　　　△ＡＰＦ∽△ＰＢＦ

（２）　（１）から実は、Ｑ＝Ｍである。（Ｒも同様）　このことから（２）は自明だろう。　　（証終）


　上記の（１）より、△ＡＰＦ∽△ＰＢＦ　なので、　ＡＦ/ＰＦ＝ＰＦ/ＢＦ　すなわち、

　　　　ＰＦ²＝ＡＦ・ＢＦ

が成り立つ。さらに、次の性質も美しい。

　準線上の点Ｐから引いた接線の接点を結ぶ直線は焦点を通る。

　上図で、ＡＦとＢＦは一般には折れ線になるが、Ｐが準線上にあるとき、３点Ａ、Ｆ、Ｂは同一
直線上に並ぶというわけだ。

　幾何的には、∠ＡＦＢ＝２（∠ＡＰＦ＋∠ＢＰＦ）＝１８０°から明らかであるが、解析的な証
明にも取り組んでみよう。

（証明）　放物線を ｙ²＝４ｐｘ とすると、焦点Ｆ（ｐ，０）である。

　接点Ａ（ｐｍ²，２ｐｍ）、Ｂ（ｐｎ²，−２ｐｎ）　（ｍｎ≠０）における接線の方程式は、

　２ｐｍｙ＝２ｐ（ｘ＋ｐｍ²）、 −２ｐｎｙ＝２ｐ（ｘ＋ｐｎ²）　すなわち、

　　　　ｍｙ＝ｘ＋ｐｍ²、 ｎｙ＝−ｘ−ｐｎ²　である。

　辺々加えて、　（ｍ＋ｎ）ｙ＝ｐ（ｍ−ｎ）（ｍ＋ｎ）　より、　ｙ＝ｐ（ｍ−ｎ）

　このとき、　ｍｐ（ｍ−ｎ）＝ｘ＋ｐｍ²　より、ｘ＝−ｍｎｐ

　Ｐは準線上にあるので、　−ｍｎｐ＝−ｐ　すなわち、　ｍｎ＝１　が成り立つ。

　直線ＡＢの式において、ｍ＝ｎ のとき、Ａ（ｐｍｎ，２ｐｍ）、Ｂ（ｐｍｎ，−２ｐｍ）　すなわち、

　Ａ（ｐ，２ｐｍ）、Ｂ（ｐ，−２ｐｍ）となり、明らかに直線ＡＢは焦点Ｆを通る。

　ｍ≠ｎ のとき、傾きが２ｐ（ｍ＋ｎ）/ｐ（ｍ²−ｎ²）＝２/（ｍ−ｎ）　より、

　ｙ＝｛２/（ｍ−ｎ）｝（ｘ−ｐｍ²）＋２ｐｍ
　 ＝｛２/（ｍ−ｎ）｝ｘ−２ｐｍｎ/（ｍ−ｎ）＝｛２/（ｍ−ｎ）｝ｘ−２ｐ/（ｍ−ｎ）

　ｘ＝ｐ　のとき、ｙ＝０ となり、直線ＡＢは焦点Ｆを通る。　　（証終）

　　　　　　

　また、次の事実も上図より明らかだろう。

　準線上の点から放物線に引いた２本の接線は垂直である。

　∠ＤＰＥ＝１８０°なので、∠ＡＰＢ＝９０°となる。

　逆に、

　放物線に、互いに直交する２本の接線を引くとき、その交点は準線上にある。
また、交点と２接点の中点を通る直線は準線に直交する。

　前半は、上図から明らかだろうが、後半も含めて解析的に示そう。

（証明）　放物線を ｙ²＝４ｐｘ とし、接点Ａ（ｐｍ²，２ｐｍ）、Ｂ（ｐｎ²，−２ｐｎ）　（ｍｎ≠０）にお

　ける接線の方程式は、　２ｐｍｙ＝２ｐ（ｘ＋ｐｍ²）、 −２ｐｎｙ＝２ｐ（ｘ＋ｐｎ²）　すなわち、

　ｍｙ＝ｘ＋ｐｍ²、 ｎｙ＝−ｘ−ｐｎ²　である。これらが垂直なので、ｍｎ＝１ が成り立つ。

　辺々加えて、　（ｍ＋ｎ）ｙ＝ｐ（ｍ−ｎ）（ｍ＋ｎ）　より、　ｙ＝ｐ（ｍ−ｎ）

　このとき、　ｍｐ（ｍ−ｎ）＝ｘ＋ｐｍ²　より、ｘ＝−ｍｎｐ＝−ｐ

　よって、Ｐは、準線上にあり、その座標は、Ｐ（−ｐ，ｐ（ｍ−ｎ））

　さらに、線分ＡＢの中点のｙ座標は、　（２ｐｍ−２ｐｎ）/２＝ｐ（ｍ−ｎ）　となることから、交点

　と２接点の中点を通る直線は準線に直交する。　　（証終）


　上記の更なる一般の場合として、次の事実も面白い。

　放物線上の異なる３点Ａ、Ｂ、Ｃについて、点Ａにおける接線と点Ｃにおける接線との交点
をＰ、点Ｂにおける接線と点Ｃにおける接線との交点をＱ、点Ａにおける接線と点Ｂにおける
接線との交点をＲとする。このとき、

　　△ＰＱＲの外接円は、放物線の焦点を通る。

　Ｃが放物線の頂点の場合を考えれば、これまでに示したことであるが、実は、Ｃが頂点で
ない場合も言えるという点が興味深い。

　この事実を示すには、円周角の定理の逆が用いられる。

（証明）　放物線の焦点をＦとし、Ａから準線に下ろした垂線の足をＡ’とすれば、ＡＦ＝ＡＡ’

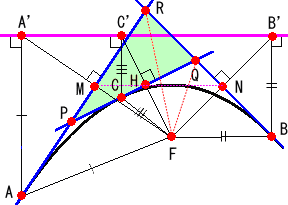　　　また、放物線の性質から、Ａにおける接
　　線は、∠ＦＡＡ’を２等分するので、ＡＭは
　　ＦＡ’の垂直２等分線となる。

　　　同様に、Ｂから準線に下ろした垂線の足
　　をＢ’、Ｃから準線に下ろした垂線の足をＣ’
　　とすれば、ＢＮはＦＢ’の垂直２等分線、ＣＨ
　　はＦＣ’の垂直２等分線となる。

　　　ここで、中点連結定理より、Ｍ、Ｎ、Ｈも同
　　一直線上にある。

　また、∠ＦＭＲ＝∠ＦＮＲ＝９０°であるから、四角形ＭＦＮＲは同一円周上にあり、
∠ＲＮＭ＝∠ＲＦＭ　すなわち、∠ＲＮＭ＝∠ＱＮＨである。

　∠ＱＨＦ＝∠ＱＮＦ＝９０°であるから、四角形ＦＮＱＨは同一円周上にあるので、
∠ＱＮＨ＝∠ＱＦＨが成り立つので、よって、∠ＲＦＭ＝∠ＱＦＨである。

　∠ＲＰＱ＝θ　とおくと、図から明らかに、∠ＨＦＭ＝θ

　ここで、∠ＲＦＭ＝∠ＱＦＨ　より、　∠ＲＦＭ＋∠ＨＦＭ＝∠ＲＦＭ＋∠ＲＦＱ　なので、

　∠ＲＦＱ＝∠ＨＦＭ＝θ

　従って、∠ＲＰＱ＝∠ＲＦＱ　となり、これは、Ｆが△ＰＱＲの外接円上にあることを示す。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（証終）

　放物線と言えば、共通接線の話題が有名だろう。次の性質も興味深い。

　２つの放物線 ｙ＝ａｘ²　、ｙ＝ａ（ｘ−ｐ）²＋ｑ の共通接線の傾きは、ｑ/ｐ である。

　２つの放物線は同形なので、その頂点（０，０）、（ｐ，ｑ）を結ぶ直線の傾きと共通接線の傾
きが同じだろうことは想像に難くない。しかし、いざ証明しようとすると、少し大変かもしれない。

（証明）　共通接線の方程式を ｙ＝ｍｘ＋ｎ とし、それぞれの接点の ｘ 座標を α、β とおくと、

　ａｘ²−（ｍｘ＋ｎ）＝ａ（ｘ−α）²　より、　ｍ＝２ａα　、ｎ＝−ａα²

　ａ（ｘ−ｐ）²＋ｑ−（ｍｘ＋ｎ）＝ａ（ｘ−β）²　より、　２ａｐ＋ｍ＝２ａβ　、　ａｐ²＋ｑ−ｎ＝ａβ²

　よって、　ｍ＝２ａ（β−ｐ）＝２ａα　より、　β−ｐ＝α　であり、また、　β−α＝ｐ

　このとき、

　　ｍ＝｛ａ（β−ｐ）²＋ｑ−ａα²｝/（β−α）＝｛ａα²＋ｑ−ａα²｝/（β−α）＝ｑ/ｐ

が成り立つ。　　（証終）

　この事実を知っていれば、次のような問題に応用できるだろう。

例　２つの放物線 ｙ＝ｘ²　、ｙ＝（ｘ−２）²＋４ の共通接線の方程式を求めよ。

（解）　放物線 ｙ＝ｘ² の接点の ｘ 座標を α とおくと、接線の傾きは、２αで、これが共通接

　　線の傾き ２ に等しいので、　２α＝２　より、　α＝１　　よって、接点（１，１）

　　これより、共通接線の方程式は、　ｙ＝２（ｘ−１）＋１＝２ｘ−１　となる。　　（終）


　もし、上記の事実を知らなければ、次のような計算をするのだろう。

（別解）　共通接線の方程式を ｙ＝ｍｘ＋ｎ とし、それぞれの接点の ｘ 座標を α、β とおくと、

　　　　ｘ²−（ｍｘ＋ｎ）＝（ｘ−α）²　より、　ｍ＝２α　、ｎ＝−α²

　　　（ｘ−２）²＋４−（ｍｘ＋ｎ）＝（ｘ−β）²　より、　４＋ｍ＝２β　、　４＋４−ｎ＝β²

　　　よって、　β−α＝２　、　β²−α²＝８　より、　β＋α＝４

　　　これより、　α＝１、β＝３　となり、　ｍ＝２、ｎ＝−１　なので、

　　　求める共通接線の方程式は、　ｙ＝２ｘ−１　となる。　　（終）


(コメント）　公式の有り難みが実感できますね！


　ところで、放物線 ｙ＝ａｘ² に点Ｐから引いた接線の接点の ｘ 座標を、α、β とすると、点
Ｐの ｘ 座標が、（α＋β）/２ で与えられることは有名であるが、同様なことが、２つの放物
線が共通接線を持つときにも起こる。すなわち、

　２つの放物線と共通接線の接点の ｘ 座標を、α、β とすると、２つの放物線の交
点の ｘ 座標は、（α＋β）/２　で与えられる。

（証明）　２つの放物線を ｙ＝ａｘ²、ｙ＝ａ（ｘ−ｐ）²＋ｑ 、共通接線の方程式を ｙ＝ｍｘ＋ｎ と

　し、それぞれの接点の ｘ 座標を α、β とおく。

　このとき、　ａ（ｘ−ｐ）²＋ｑ＝ａｘ²　より、　−２ａｐｘ＋ａｐ²＋ｑ＝０

　よって、　２ｘ＝（ａｐ＋ｑ/ｐ）/ａ＝（ａβ−ａα＋ｍ）/ａ＝（ａβ−ａα＋２ａα）/ａ＝α＋β

　より、　ｘ＝（α＋β）/２　となる。


（コメント）　これは全くの偶然なのか、それとも意味があることなのだろうか？


　　　以下、工事中！