
このページは、日頃からお世話になっている広島工業大学の大川研究室が出題した数学
の演習問題に対する解答をまとめたものである。興味を引く問題も多数含まれるので、一般
の方も是非挑戦してほしいと思う。
数学演習 
このページは、日頃からお世話になっている広島工業大学の大川研究室が出題した数学
の演習問題に対する解答をまとめたものである。興味を引く問題も多数含まれるので、一般
の方も是非挑戦してほしいと思う。
| 回 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 内容 | 不等式 | 連続・不連続 | 極限 | 微分1 | 微分2 | 逆関数 | 導関数 |
| 回 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 内容 | 極限値 | テイラー展開 | 極値・級数 | 不定積分 | 定積分 | 面積・長さ | 広義積分 |
問題1.1 次の集合を2通りの表し方で表せ。
n が3以上7以下の自然数のとき、n2 で表される数の全体
(答) {9,16,25,36,49} または { x | x=n2 ただし、nは自然数で、3≦n≦7}
問題1.2 次の条件を満たす x の集合を区間(の和集合)を用いて表せ。
(1) | x−5|<3 (2) x2 >4
(答) (1) 開区間 (2,8) (2) 開区間 (−∞,−2)∪(2,∞)
問題1.3 次の等式が x についての恒等式になるように a , b , c を定めよ。
![]()
(答) 通分して、分子を比較すれば、(a+b)x2+cx+a=1 より、a=1,b=−1,c=0
問題1.4 次の不等式を解け。
![]()
| (答) | 不等式を等式に変え、分母を払って、両辺を平方すれば、 (x+2)2=16(x−1) この2次方程式の解は、 (x−2)(x−10)=0 より、x=2,10 したがって、左図より、解は、 2<x<10 |
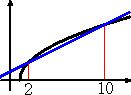 |
問題1.5 次の不等式を証明せよ。( a,b は実数) : |ab|≦(9/2)a2+(1/18)b2
(答) 相加平均と相乗平均の関係から、右辺≧2√((9/2)a2・(1/18)b2)=左辺
等号成立は、9a=b のときに限る。
問題1.6 次の数列の極限値を求めよ。
| (1) | |
(2) | |
(3) | |
| (4) | |
(5) | |
||
(答) (1) 3/2 (2) 0 (3) +∞ (4) 16 (5) 1/2
問題1.7 次の集合を求めよ。
(1) (1,5)∩[2,8] (2) {[1,3]∪(0,8)}∩[−1,9]
(3) [3,11)∩[0,7)∩(2,9]
(答) (1) [2,5) (2) (0,8) (3) [3,7)
問題1.8 1≦x≦8,−3<y<2 のとき、x−y2 はどの範囲にあるか?
(答) 0≦y2<9 より、−9<y2≦0 したがって、−8<x−y2<8
問題1.9 ( ← この問題は面白かったです...。)
(1) 正の実数 x を小数表示し、小数第2位を四捨五入して得られた数の小数第1位を
四捨五入して得られた数が丁度3になった。元の x はどの範囲にあるか?
(2) 正の実数 x を小数表示し、その数を5倍してから小数第2位を切り捨てて得られた
数を7で割った数の小数第1位を切り上げて得られた数が丁度3になった。元の
x
はどの範囲にあるか?
(答) (1) 正の実数 x を小数表示し、小数第2位を四捨五入して得られた数を、y とお
くと、題意より、y は、2.5,2.6,・・・,3.4 のいずれか。
したがって、求める x の範囲は、
[2.45,2.55)∪[2.55,2.65)∪・・・∪[3.35,3.45)
=[2.45,3.45)
すなわち、 2.45≦ x <3.45 が求める x の範囲である。
(2) 正の実数 x を小数表示し、その数を5倍してから小数第2位を切り捨てて得ら
れた数を、y とおく。題意より、 2.1≦ y/7 ≦3 なので、
14.7≦ y ≦21
したがって、 14.7≦ 5x <21.1 より、 2.94≦
x <4.22
第2回(連続・不連続)
問題2.1 平面上で、点(2,3)を通り、原点からの距離が1である直線の方程式を求めよ。
(答) 求める直線の方程式は、y=a(x−2)+3 とおける。点と直線の距離の公式から、
|
|
これを解いて、 |
問題2.2 次の極限値を求めよ。
| (1) | |
(2) | |
(答) (1) 1 (2) 1
問題2.3 (1) 次の関数の連続点、不連続点を求めよ。(注 [ x ] はGaussの記号)
f(x) = x3+[ x+1 ]
(2) 次の関数の連続点、不連続点を求めよ。
f(x) = ( | x |+1/2+[ x ] )2
(答)
| (1) | x が整数のとき、不連続、 それ以外のとき、連続 |
(2) | x が自然数のとき、不連続、 それ以外のとき、連続 |
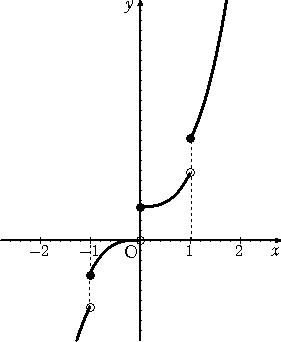 |
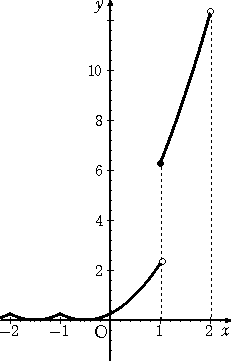 |
||
問題2.4 次の関数のグラフの概形を書け。
f(x) = −x+[ x ]
(答)
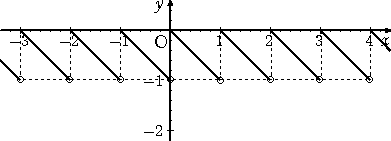
問題2.5 次の関数・数列の極限値を求めよ。
| (1) | |
(2) | |
(3) | |
(答) (1) 1/2 (2) 0 (3) 1/2
問題2.6 次の式を簡単にせよ。ただし、a>0、b>0とする。
| (1) | 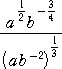 |
(2) | |
(答) (1) a1/6b-1/12 (2) ay(z+x)
第3回(極限)
問題3.1 次の式を因数分解せよ。
(1) x3−y3 (2) x4−y4
(答) (1) (x−y)(x2+xy+y2) (2) (x+y)(x−y)(x2+y2)
問題3.2 次の極限値を求めよ。
| (1) | 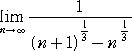 |
(2) | |
(答) (1) +∞ (2) 1
問題3.3 次の連続関数 f(x) = ax+b+c| x−3 | が、x≦3 で、傾き3の1次関数、
3≦x で、傾き5の1次関数、f(3) = 2 のとき、a、b、c を求めよ。
(答) 題意より、a−c=3 、a+c=5 、3a+b=2 よって、a=4、b=−10、c=1
問題3.4 実数全体で定義された関数で、3で不連続で、他で連続な関数の具体例を1つ
求めよ。
(答) たとえば、無限級数で表された関数
![]()
問題3.5 次の関数・数列の極限値を求めよ。
| (1) | |
(2) | |
(3) | |
(答) (1) 1 (2) −∞ (3) −∞
問題3.6
(1) 問題3.3の関数 f(x) の逆関数 g(x) を求めよ。
(2) 合成関数 f(g(x+1)−1) を求めよ。
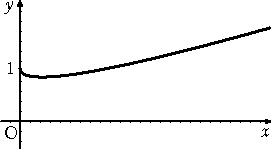
(3) 次の関数の自然な定義域と値域を求めよ。
![]()
(答) (1) x≧3 のとき、y=f(x)=5x−13 より、 y≧2 で、 x=(1/5)y+13/5
したがって、x と y を交換して、x≧2 のとき、y=(1/5)x+13/5
すなわち、 g(x)=(1/5)x+13/5
同様にして、 x≦2 のとき、g(x)=(1/3)x+7/3
上記を一つの式で表すには、
g(x) = ax+b+c| x−2 |
とおいて、 a+c=1/5 、a−c=1/3 、g(2) = 3 を解けばよい。
このとき、 a=4/15 、c=−1/15 、b=37/15
よって、 g(x) = (4/15)x+37/15−(1/15)| x−2 |
(2) g(x) は、x=2 の前後で関数の形が変わるので、g(x+1)
は、x=1 の前後
で関数の形が変わる。ところで、f(x) は、x=3 の前後で関数の形が変わるので、
g(x+1)−1=3 となる x の値を求める必要がある。g(2)
= 3 に注意して、
g(x+1)=4 であるので、 (1/5)(x+1)+13/5=4
これを解いて、x=6 となる。
よって、x≧6 のとき、 g(x+1)−1≧3 、x+1≧7≧2 なので、
f(g(x+1)−1)=5(g(x+1)−1)−13
=5g(x+1)−18
=5((1/5)x+14/5)−18= x−4
1≦x≦6 のとき、 g(x+1)−1≦3 、x+1≧2 なので、
f(g(x+1)−1)=3(g(x+1)−1)−7
=3g(x+1)−10
=3((1/5)x+14/5)−10= (3/5)x−8/5
x≦1 のとき、 g(x+1)−1≦3 、x+1≦2 なので、
f(g(x+1)−1)=3(g(x+1)−1)−7
=3g(x+1)−10
=3((1/3)x+8/3)−10= x−2
上記を一つの式で表すには、
g(x) = ax+b+m| x−1 |+n| x−6 |
とおいて、 a−m−n=1 、a+m+n=1 、a+m−n=3/5 を解けばよい。
このとき、 a=1 、b=−3 、m=−1/5 、n=1/5
よって、 f(g(x+1)−1)=x−3−(1/5)| x−1 |+(1/5)|
x−6 |
(3) 定義域は、 x≧0 、 値域は、 y≧15/16
第4回(微分1)
問題4.1 関数を微分せよ。
| (1) | |
(2) | |
(3) | |
(答) (1) f(x)=x10+x5+1 なので、f’(x)=10x9+5x4
(2) f(x)=x+1/(x+1) なので、f’(x)=1−1/(x+1)2
(3) f’(x)=100(4x+1)(2x2+x+3)99
問題4.2 次の各直線の方程式を求めよ。
(1) 曲線 y=x3−3x+1 の y 軸との交点における接線の方程式を求めよ。
(2) 曲線 y=x3−x+1 の点(1,1)を通る接線の方程式を求めよ。
(答) (1) 接点(0,1)より、y’=3x2−3=−3 なので、接線の方程式は、y=−3x+1
(2) y’=3x2−1=2 なので、接線の方程式は、y=2(x−1)+1=2x−1
問題4.3 次の連続関数 f(x) = ( | x−1 |− | x |+ | x+1 |−2
)2 の微分可能な点を
調べ、導関数を求めよ。
(答) x≦−1 のとき、 f(x) =( x+2 )2 、−1≦x≦1 のとき、 f(x) =x2
x≧1 のとき、 f(x) =( x−2 )2 なので、x=1,−1 以外で微分可能。
導関数は、x≦−1 のとき、 f’(x) =2( x+2 )、−1≦x≦1 のとき、 f’(x)
=2x
x≧1 のとき、 f(x) =2( x−2 )
(参考)
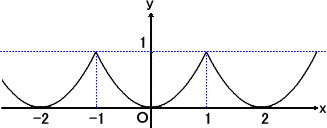
(コメント: パッと見で、x=0 で微分できないと予想しましたが、以外にも微
分可能なのですね。驚きました!これも自乗の効果なのですね。)
問題4.4 実数全体で定義された連続関数で、3で微分不可能で、他で微分可能な関数
の具体例を1つ求めよ。
(答) 具体例の一つとして、 f(x) = | x−3 |
問題4.5 次の関数の導関数を積の微分の公式から求めよ。
![]()
(答) y=f(x) とおくと、 y・y =x なので、両辺を x について微分すれば、y’・y+y・y’=1
よって、 y’=1/(2y)=1/(2√x)
問題4.6 次の関数の導関数を逆関数の導関数の公式から求めよ。
| (1) | |
(2) | |
(答) (1) y=f(x) とおくと、 x=y2 なので、dy/dx=1/(dx/dy)=1/(2y)=1/(2√x)
(2) y=f(x) とおくと、 x=y3 なので、dy/dx=1/(dx/dy)=1/(3y2)=1/(3x2/3)
問題4.7
| (1) | f(x)=sin(6x+1) の導関数を求めよ。 |
| (2) | f(x)=sec(x2+1) の導関数を求めよ。 |
(答) (1) f’(x) =6cos(6x+1)
(2) f’(x) =2x・sec(x2+1)・tan(x2+1)
問題4.8 x=sin t 、y=cos t 、5< t <6 のとき、dx/dy を
y の式として求めよ。
(答) dx/dy =(cos t )/(−sin t ) において、5< t <6 のとき、sin
t <0 なので、
sin t =−√(1−cos2t) =−√(1−y2) よって、 dx/dy = y/√(1−y2)
(コメント:問題文の注釈に、「t の範囲によって符号が変わることに注意」とあります
が、符号は変わらないと思うのですが...?)
→ 負の符号になるという意味だそうです。
第5回(微分2)
問題5.1 関数を微分せよ。
| (1) | |
(2) | |
(3) | |
| (4) | |
(5) | |
(6) | |
| (7) | |
(8) | |
(9) | |
| (10) | |
(11) | |
||
| (12) | |
||||
| (13) | |
(14) | (13)の関数の導関数をもう一度微分せよ。 | ||
(答) (1) x/(x2+1) (2) log x (3) 2・1002x+3log 100 (4) n(log x)n−1/x
(5) −2xe(−x2+1) (6) xx(log x+1)
(7) (3log(2x+1)+(6x−2)/(2x+1))(2x+1)3x−1 (8) 2xlog2+3xlog3
(9) (log x−1)/(log x)2 (10) 20e20x (11) 3x2cos(log(x3+1))/(x3+1)
(12) −6x2sin(x3+1)/cos(x3+1) (13) 3x| x | (14) 6| x |
問題5.2 x=t/(t2+1) 、y=t2+1 のとき、
(1) dx/dy を求めよ。 (2) (1)の値を、y の式で求めよ。
(符号に注意。t の範囲によって場合分けをせよ。)
(答) (1) (1−t2)/(2t(t2+1)2)
(2) ±(2−y)/(2y2√(y−1)) ( t ≧ 0 のとき、+、t < 0 のとき、− )
問題5.3 x=et+2e−t 、y=et−2e−t のとき、
(1) dx/dy を求めよ。 (2) (1)の値を、y の式で求めよ。
(答) (1) (et−2e−t)/(et+2e−t) (2) x >0 に注意して、 y/√(y2+8)
(コメント: 導関数を「値」と表現することに違和感を覚えました。また、媒介変数表示の場
合の導関数の計算は、高校では通常 dy/dx を求める場合が多いのですが、
問題のように、dx/dy を求めさせることに、何か意図があるのでしょうか?)
第6回(逆関数)
問題6.1 次の逆三角関数の値を求めよ。
(1) sin-11 (2) sin-1(−1) (3) sin-1(1/2) (4) cos-11
(5) cos-1(1/2) (6) tan-1√3 (7) tan-1(−1/√3)
(8) sin-1(√6−√2)/4 (9) sin-1(1/√2)
(答) (1) π/2 (2) −π/2 (3) π/6 (4) 0 (5) π/3
(6) π/3 (7) −π/6 (8) π/12 (9) π/4
問題6.2 次の関数の導関数を求めよ。
(1) y=sin-1x (2) y=cos-1x (3) y=tan-1x (4) y=(sin-1x)3
(5) y=sin-1x3 (6) y=tan-1(x+1)2 (7) y=cos(2cos-1x)
(8) y=log√(x4−1)−log√(x2−1)
(答) (1) 1/√(1−x2) (2) −1/√(1−x2) (3) 1/(1+x2)
(4) 3(sin-1x)2/√(1−x2) (5) 3x2/√(1−x6)
(6) 2(x+1)/(1+(x+1)4)
(7) 倍角の公式から、cos(2cos-1x)=2cos2(cos-1x)−1=2x2−1 なので、
導関数は、4x となる。
(8) y=log√(x2+1) であるので、導関数は、 x/(1+x2)
問題6.3
(1) 次の等式を示せ。
|
|
( xy<1 ) |
(2) 次の関数を微分せよ。

(答) (1) A=tan-1x 、B=tan-1y とおく。ただし、 −π/2<A、B<π/2 である。
このとき、 x=tanA 、y=tanB なので、
(x+y)/(1−xy)=(tanA+tanB)/(1−tanA・tanB)=tan(A+B)
ところで、 −π<A+B<π なので、±πという定数差を無視して、
A+B=tan-1(x+y)/(1−xy) が成り立つ。
(コメント) 「 tan(tan-1x+tan-1y)=(x+y)/(1−xy) を示せ。」という問題の方が無難
かもしれないですね。
(2) (−x2−1+2(x+1)√x)/2(x3+x2+x+1)√x
問題6.4 次の関数 f(x) の逆関数 f-1(x) の導関数を求めよ。(x の式で表せ。)
f(x) = cos x + sin x
(答) f(x) = √2・ sin( x+π/4) なので、 f-1(x) = −π/4+sin-1(x/√2)
したがって、 その導関数は、 (1/√2)/√(1−x2/2) = 1/√(2−x2) である。
第7回(導関数)
問題7.1 次の各関数の第2次導関数を求めよ。
(1) y=xx (2) y=arcsin x (3) y=(log x)2 (4) y=cos(x2+1)
(5) y=loglog x
(答) (1) xx-1(x(log x+1)2+1) (2) x/(1−x2)√(1−x2) (3) 2(1+log x)/x4
(4) −2sin(x2+1)−4x2cos(x2+1) (5) −(log x+1)/(xlog x)2
問題7.2 次の関数の第12階導関数を求めよ。 y=(x15−1)/(x3−1)
(答) y=x12+x9+x6+x3+1 より、y(12)=12!
問題7.3 次の各関数の第n階導関数を求めよ。
(1) y=cos(3x+1) (2) y=√(2x+1) (3) y=x/(x2−1)
(4) y=log√(3x+1) (5) y=log√(x2−3x+2)
(6) y=ex/x (7) y=sin x cos x (8) y=cos2 x − sin2 x
(答) (1) 3n・cos(3x+1+nπ/2)
(2) (1/2)((1/2)−1)・・・((1/2)−n+1)(2x+1)(1/2)−n2n
または、(−1)n-1(2n−3)!(2x+1)(1/2)−n/(2n-2(n−2)!)
(コメント:答の最終形として、どちらが適切であろうか?個人的には、前者で十分
と思うが...?)
(3) y=(1/(x+1)+1/(x−1))/2 であることに注意して、
y(n)=(−1)nn!(1/(x+1)n+1+1/(x−1)n+1)/2
(4) y(n)=−(−3)n(n−1)!/(2(3x+1)n)
(5) y(n)=(−1)n-1(n−1)!(1/(x−1)n+1/(x−2)n)/2
(6)
![]()
(7) y=(1/2)sin 2x なので、 y(n)=2n-1・sin(2x+nπ/2)
(8) y=cos 2x なので、 y(n)=2n・cos(2x+nπ/2)
第8回(極限値)
問題8.1 次の極限値を求めよ。
| (1) | |
(2) | |
(3) | |
| (4) | |
(5) | |
(6) | |
| (7) | |
(8) | |
||
| ( a は定数) | ( α、β は定数) |
(答) (1) 1/2 (2) 5 (3) 1 (4) −1/6 (5) 1/3 (6) 1
(7) a<1/6 のとき、+∞ 、 a=1/6 のとき、 −1/120 、
a>1/6 のとき、−∞
(8) β>1 のとき、−∞ 、β=1 のとき、α(α−1)/2 、β<1 のとき、+∞
問題8.2 次の数列の極限値を求めよ。
![]()
注意 ロピタルの定理を使うには、その前提条件が満たされていることを示さねばならない。
ヒント f(x)=logxとg(x)=√xに区間[n,n+1]でコーシーの平均値の定理を用いて各項を評価して
もよい。
| (答) | |
(コメント:ロピタルの定理を用いてもできますが、上記のような式変形で求める方が自然だ
と思います。)
問題8.3 f(x)を閉区間[a,b]で3回連続微分可能な関数とする。
f(a)=f’(a)=f(b)=f’(b)=0 とする。
このとき、 a < c < b なる c で、f”’(c)=0 なる点
c が存在することを示せ。
(答) 平均値の定理から、
f(a)=f(b)=0 より、 f’(p)=0 ( a < p <
b ) なる点 p が存在する。
同様に、
f’(a)=f’(p)=0 より、 f”(q)=0 ( a < q
< p ) なる点 q が存在する。
f’(b)=f’(p)=0 より、 f”(r)=0 ( p < r < b ) なる点 r が存在する。
したがって、
f”(q)=f”(r)=0 より、 f”’(c)=0 なる点 c が存在し、
a < q < c < r < b を満たす。
第9回(テイラー展開)
問題9.1 次の関数の第 n 階導関数を求めよ。
(1) y=(xex)3 (2) y=sinh x
(答) (1) 3n-3e3x(27x3+27nx2+9n(n−1)x+n(n−1)(n−2))
(2) (ex−(−1)ne−x)/2
問題9.2
(1) f(x) = tan x のマクローリン展開において、最初の0でない3項を求めよ。
(2) f(x) = sin x を x= π でテイラー展開せよ。
(3) f(x) = 1/x を x= 7 でテイラー展開せよ。
(4) f(x) = 2x+3x をマクローリン展開せよ。また、x= 1 でテイラー展開せよ。
(5) f(x) = log x を x= 10 でテイラー展開せよ。
| (答) | (1) | (2) | (3) | |||
| (4) | |
|||||
| テイラー展開は、 | ||||||
| (5) | |
|||||
問題9.3 関数 f(x) = x3−3x の半開区間(−1,2] での最大・最小、極大・極小を求
めよ。
(答) x=2 のとき最大で、最大値 2 、x=1 のとき最小で、最小値 −2
x=1 のとき極小で、極小値 −2 、極大値はない。
問題9.4 関数 f(x) = x3−3x2−3x の極大値と極小値の和と積を求めよ。
(ヒント。 極値をとる点 α、β は、方程式 f’(x) = 0 の解である。f(x)
を f’(x) で割り
算した(f’(x)/3 で割っても同じ)余りを h(x) (これは高々1次式)とおくと、f(x)
の極値は、h(α)、h(β) となる。更に、解と係数の関係を使う。)
(答) f’(x) = 3x2−6x−3=0 は、判別式 D/4=9+9=18>0 より、相異なる2つ
の解 α、β を持つ。
関数 f(x) の増減を調べることにより、 極値は、f(α) と f(β)
である。
ところで、 f(x) =(x−1)(f’(x)/3)−4x−1 なので、
f(α) = −4α−1 、 f(β) = −4β−1
解と係数の関係より、 α+β=2 、αβ=−1 なので、
極大値と極小値の和
= f(α) + f(β) =−4α−1−4β−1=−4(α+β)−2=−10
極大値と極小値の積
= f(α)f(β) =(−4α−1)(−4β−1)=16αβ+4(α+β)+1=−7
問題9.5 関数 f(x) = cos-1(1−x2)+5x/2 の −![]() ≦x≦
≦x≦![]() における最大・最小、
における最大・最小、
極大・極小について調べよ。
(この範囲内に微分不可能な点が3つあることに注意。)
(答) x=−![]() 、0 、
、0 、 ![]() の3点で微分不可能である。
の3点で微分不可能である。
x=![]() のとき最大で、最大値 π+5/
のとき最大で、最大値 π+5/![]()
x=−(√34)/5 のとき極小かつ最小で、
極小値(最小値)は、cos-1(−9/25)−(√34)/2
極大値はない。
(コメント: 第9回の問題は、煩雑な計算を必要とする問題が多かったですね。特に、問題
9.2 (1)は計算に自信がなかったので、ベッセル関数を用いる方法で検算して
しまいました。 問題9.5 において、最大・最小にしろ、極大・極小にしろ微分可
能性とは全く関係なしに求められるわけですので、殊更、微分不可能な点が3つ
あることに注意という但書きは必要がないと思われますが...。)
第10回(極値・級数)
問題10.1 x>0 のとき、次の不等式を証明せよ。
(1) ex>1+x+x2/2 (2) (2−2x+x2)/2>e−x (3) sinh x > x > tanh x
(答) (1) f(x)=ex−(1+x+x2/2) とおくと、
f’(x)=ex−(1+x) 、 f”(x)=ex−1 、 f”’(x)=ex>0
よって、f”(x)は単調増加で、f”(0)=0 より、x>0 のとき、f”(x)>0
よって、f’(x)は単調増加で、f’(0)=0 より、x>0 のとき、f’(x)>0
よって、f(x)は単調増加で、f(0)=0 より、x>0 のとき、f(x)>0
したがって、 ex>1+x+x2/2
(2) f(x)=(2−2x+x2)/2−e−x とおくと、
f’(x)=−1+x+e−x 、 f”(x)=1−e−x 、 f”’(x)=e−x>0
よって、f”(x)は単調増加で、f”(0)=0 より、x>0 のとき、f”(x)>0
よって、f’(x)は単調増加で、f’(0)=0 より、x>0 のとき、f’(x)>0
よって、f(x)は単調増加で、f(0)=0 より、x>0 のとき、f(x)>0
したがって、 (2−2x+x2)/2>e−x
(3) f(x)=sinh x − x 、 g(x)=x − tanh
x とおくと、
f’(x)=cosh x −1≧0 より、f(x)は単調増加で、f(0)=0 より、
x>0 のとき、f(x)>0 すなわち、 sinh x >
x
同様にして、
g’(x)=1−sech2 x ≧0 より、g(x)は単調増加で、g(0)=0 より、
x>0 のとき、g(x)>0 すなわち、 x > tanh
x
問題10.2 次の関数の極大・極小について調べよ。
(1) f(x)=x6−3x2+1 (2) f(x)=xe−x (3) f(x)=| x+1 |−| x |+| x−1 |
(答) (1) 極大値 1 (x=0 のとき) 極小値 −1 (x=1、−1 のとき)
(2) 極大値 1/e (x=1 のとき) 極小値はない
(3) 極大値 2 (x=0 のとき) 極小値 1 (x=1、−1 のとき)
問題10.3 次の有限級数の和を求めよ。
| (1) | |
(2) | |
(ヒント: 公比 x の等比級数の和の公式を使い、両辺を微分する。勿論、分母が出てくる
場合は、それが 0 になる場合を検討する必要がある。)
(答) (1) 与式=S とおくと、 (1−x)S=x+x2+x3+・・・+xn−nxn+1
よって、x≠1 のとき、 S=(x−(n+1)xn+1+nxn+2)/(1−x)2
x=1 のとき、 S=n(n+1)/2
(2) rnCr=nn−1Cr−1 なので、与式=nx(1+x)n−1
問題10.4 次の関数での極座標におけるグラフの概形を書け。
(この場合、r
<0 でもよいことに注意)
(1) r=2−θ (対数スパイラル)
さらに、このグラフを原点を中心として相似拡大したグラフは、自分自身に合同であ
ることを示せ。
(2) r=cos(θ+π/6)
さらに、θが動くとき、グラフが自分に重ならないようなθの最小範囲を一つ求めよ。
(答) (1)
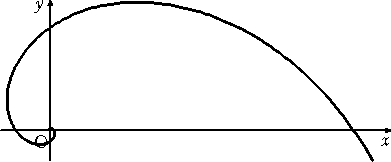
後半部分は、2−(θ+2kπ)=2−2kπ× r から明らか。
(2)
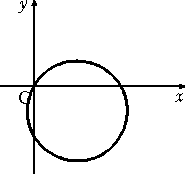 |
左図は、中心の座標 ( 半径 1/2 の円である。 また、求める θ の範囲は、 0 ≦ θ < π である。 |
問題10.5 次の有限級数の和を求めよ。
| (1) | |
(2) | |
(ヒント: 等比級数の和の公式で、公比を reiθ ( i は虚数単位)として、オイラーの公式を
用いて、両辺の実部、虚部を比較する。解答を完全に整理する必要はないが、分母
を生じた場合は、それが 0 になる場合の検討を要する。)
(答) reiθ≠1 のとき、
(1) (1−rcosθ−rn+1cos(n+1)θ+rn+2cosnθ)/(1+r2−2rcosθ)
(2) (rsinθ−rn+1sin(n+1)θ+rn+2sinnθ)/(1+r2−2rcosθ)
reiθ=1 のとき、 (1) n (2) 0
第11回(不定積分)
問題11.1 次の関数の不定積分を求めよ。
(1) f(x)=1/((x+1)2+4) (2) f(x)=(1−x4)/(1−x3)
(3) f(x)=log(3x+1) (4) f(x)=log√(x+1)
(5) f(x)=1/(1+x−x2) (6) f(x)=sinh x
(7) f(x)=(cosh x)3 (8) f(x)=(tan−1x)/(x2+1)
(9) f(x)=1/((x2+1)tan−1x) (10) f(x)=sin x cos x
(11) f(x)=sin x sin ![]() x (12) f(x)=(sin x)
x (12) f(x)=(sin x)![]() cos x
cos x
( 0<x<π/2 )
(答) 以下で、積分定数は省略する。
(1) (1/2)tan−1((x+1)/2) (2) (1/2)x2+2x+log(x2−x+1)
(3) (1/3)((3x+1)log(3x+1)−(3x+1))
(4) (1/2)((x+1)log(x+1)−(x+1))
(5) (1/√5)log | ((√5)−1+2x)/((√5)+1−2x)
| (6) (1/2)cosh 2x
(7) (1/3)(sinh x)3+sinh x (8) (1/2)(tan−1x)2 (9) log | tan−1x |
(10) (1/2)sin 2x (11) sin ![]() x cos x−
x cos x−![]() cos
cos ![]() x sin x
x sin x
(12) (sin x)![]() +1/(
+1/(![]() +1)
+1)
問題11.2
(1) cos x =(eix+e−ix)/2 を使うことにより、(両辺を5乗して)cos5x の不定積分
を求めよ。
(2) 複素数 z に対して、
![]()
と定義することにより、実数θに対して、 eiθ= cos θ+ i・sin θ となることを示せ。
(答) (1) (1/80)sin 5x +(5/48)sin 3x +(5/8)sin x
(2) Maclaurin展開により、
![]()
![]()
が成り立つことから、明らか。
(コメント: 問題11.2(1) は、高校数学では、倍角の公式と3倍角の公式を用いて、
cos5x=cos2x・cos3x=(1+cos x)/2・(cos 3x+3cos x)/4
=(1/16)cos 5x+(5/16)cos 3x+(5/8)cos
x
と変形してから、不定積分を求めることが多いようです。問題のヒントは、少し
計算が煩雑なような気がします。)
第12回(定積分)
問題12.1 次の定積分を求めよ。
| (1) | |
(2) | |
(3) | |
| (4) | |
(5) | |
(6) | |
| (7) | |
(答) (1) log(5/3) (2) π/4 (3) e2+2e-1 (4) π/3 (5) e2+1
(6) 21/8 (7) (e−1)/2
問題12.2 次の x の関数の導関数を求めよ。
| (1) | |
(2) | |
| (3) | |
(答) (1) 2x・sin | x | (2) 2x4 (3) (2x2cosx2−sinx2)/x2
第13回(面積・長さ)
問題13.1 次の曲線で囲まれた部分の面積を求めよ。
| (1) | |
(2) | |
| (3) | |
(4) | |
(答) (1) 1/3 (2) (2/3)e3/2−5/3 (3) 1/6 (4) 4/3
問題13.2 次の曲線の長さを求めよ。
| (1) | |
(2) | |
| (3) | |
||
(答) (1) 2![]() (2) (1/2)(eb−ea−e−b+e−a) (3) π
(2) (1/2)(eb−ea−e−b+e−a) (3) π
第14回(広義積分)
問題14.1 次の広義積分に関して、広義積分可能性を判定し、広義積分可能ならば、そ
の値を求めよ。
| (1) | |
(2) | |
(3) | |
| (4) | |
(5) | |
(6) | |
(答) (1) log2 (2) +∞ で、積分できない (3) (3/4)e-2
(4) −∞ で、積分できない (5) +∞ で、積分できない (6) 2
問題14.2 次の極限値を求めよ。
| (1) | |
(2) | |
(3) | |
(答) (1)
![]()
(2)
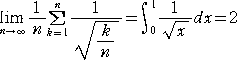
| (3) | |||
| とおくと、 | |||
![]()
よって、 与式=1/e