 丂
丂丂僩儔儞僾偺僇乕僪傪儅僕僔儍儞偼偒傟偄偵僔儍僢僼儖偡傞丅慺恖偩偲側偐側偐忋庤偔偄偐側
偄丅悽偺拞偵偼丄乽帺摦僩儔儞僾僇乕僪僔儍僢僼儖婡乿側傞傕偺偑偁傞偦偆偩偑丄偙偙偼丄儅僕
僔儍儞偵側偭偨偮傕傝偱丄庤嶌嬈偵傛傞乽僔儍僢僼儖乿偺掕媊傪偟偰偍偙偆丅
丂堦岥偵僔儍僢僼儖偲尵偭偰傕丄偄傠偄傠庬椶偑偁傞傛偆偩丅
丂僩儔儞僾偺僇乕僪傪曅庤偵帩偭偰丄嶳偺壓偐傜悢枃偢偮嶳偺忋偵堏摦偝偣傞偙偲傪孞傝曉
偡曽朄乮僸儞僘乕僔儍僢僼儖乯傗僩儔儞僾偺僇乕僪傪敿暘偢偮帩偭偰丄僇乕僪偑岎屳偵側傞傛
偆偵廳偹偰偄偔曽朄乮儕僼儖僔儍僢僼儖乯側偳偑堦斒偵抦傜傟偰偄傞丅
丂偙偺儁乕僕偱偼丄儅僕僔儍儞偑傛偔傗傞儕僼儖僔儍僢僼儖傪榖戣偵偟偨偄偲巚偆丅
丂偄傑丄僇乕僪偑 俀値 枃丂丂倎1丄倎2丄丒丒丒丄倎値丄倐1丄倐2丄丒丒丒丄倐値
偁傞偲偒丄偦偺弴彉傪暲傋懼偊偰丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 倐1丄倎1丄倐2丄倎2丄丒丒丒丒丒丒丒丒丄倐値丄倎値
偲側傞偲偒丄
丂丂丂丂丂丂丂丂丂俀値 枃偺僇乕僪偑乽僔儍僢僼儖乿偝傟偨
偲偄偆偙偲偵偡傞丅
丂丂丂丂丂丂
椺丂俀枃偺僇乕僪偵偮偄偰偼丄乮侾丄俀乯仺乮俀丄侾乯仺乮侾丄俀乯丂偲俀夞僔儍僢僼儖偡傞偲尦偵栠傞丅
椺丂係枃偺僇乕僪偵偮偄偰偼丄
丂丂丂乮侾丄俀丄俁丄係乯仺乮俁丄侾丄係丄俀乯仺乮係丄俁丄俀丄侾乯仺乮俀丆係丄侾丄俁乯仺乮侾丄俀丄俁丄係乯
丂丂偲係夞僔儍僢僼儖偡傞偲尦偵栠傞丅
椺丂俉枃偺僇乕僪偵偮偄偰偼丄
丂丂丂乮侾丄俀丄俁丄係丄俆丄俇丄俈丄俉乯仺乮俆丆侾丄俇丄俀丄俈丄俁丄俉丄係乯仺乮俈丄俆丄俁丄侾丄俉丄俇丄係丄俀乯
丂仺乮俉丄俈丄俇丄俆丄係丄俁丄俀丄侾乯仺乮係丄俉丄俁丄俈丄俀丄俇丄侾丄俆乯仺乮俀丄係丄俇丄俉丄侾丄俁丄俆丄俈乯
丂仺乮侾丄俀丄俁丄係丄俆丄俇丄俈丄俉乯丂偲俇夞僔儍僢僼儖偡傞偲尦偵栠傞丅
丂儕僼儖僔儍僢僼儖偼丄僸儞僘乕僔儍僢僼儖偵斾傋偰僇乕僪偵曃傝偑側偄愗傝曽偲偄偆報徾偑偁
傞偑丄儕僼儖僔儍僢僼儖傪壗夞偐孞傝曉偡偲尦偵栠偭偰偟傑偆惈幙偑偁傞偲偼嬃偒偱偡偹両
丂偙偺乽儕僼儖僔儍僢僼儖偺惈幙乿傪戣嵽偵偟偨栤戣偑丄暯惉侾係擭搙偺搶嫗戝妛慜婜乮棟宯乯
擖帋偱弌戣偝傟偨丅桿摫偺彫栤傕偁傞偑丄僘僶儕師偺栤偄偐偗偑娽栚偩傠偆丅
丂俀値 枃偺僇乕僪傪丄俀値 夞僔儍僢僼儖偡傞偲丄尦偵栠傞偙偲傪帵偣丅
丂丂丂乮堦斒偺帺慠悢 俀値 偵偮偄偰偺僔儍僢僼儖夞悢偼丄暿昞傪嶲徠乯
丂偙偺帠幚偑惉傝棫偪偦偆側偙偲偼丄忋婰偺椺偐傜傕柧傜偐偩傠偆丅栤戣偼丄擛壗偵偟偰帵偡
偐偱偁傞丅
丂丂俀値 枃偺僇乕僪傪丄丂侾丄俀丄丒丒丒丄値丄値亄侾丄値亄俀丄丒丒丒丄俀値丂偲弴彉傪偮偗偰暲傋丄偙偺
悢楍傪僔儍僢僼儖偟偰偱偒傞悢楍偱丄悢 倠 偑尰傟傞埵抲傪丄俥乮倠乯 偱昞偡偙偲偵偡傞丅
丂偙偺偙偲偼丄慜偐傜悢偊偰 倠 斣栚偺悢偼丄僔儍僢僼儖屻丄慜偐傜悢偊偰丄俥乮倠乯 斣栚偺埵抲
偵尰傟傞偲偄偆偙偲偱偁傞丅
丂僔儍僢僼儖偺掕媊偐傜丄
俥乮侾乯亖俀丄俥乮俀乯亖係丄丒丒丒丄俥乮値乯亖俀値丄俥乮値亄侾乯亖侾丄俥乮値亄俀乯亖俁丄丒丒丒丄俥乮俀値乯亖俀値亅侾
側偺偱丄俥乮倠乯 偺僌儔僼傪彂偗偽丄壓恾偺傛偆偵側傞丅
丂丂丂
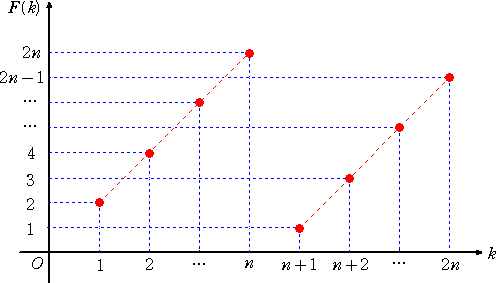
丂偙偺娭悢 俥乮倠乯 傪壗夞偐乮倣夞偲偟傛偆両乯崌惉偟偰丄丂俥倣乮倠乯亖倠丂偲側傞偙偲傪帵偣偽傛
偄丅偨偩丄俥乮倠乯 偺僌儔僼傪壗偲側偔挱傔偰偄偰傕夝寛偺巺岥偼偮偐傔側偄丅
丂俥乮倠乯 偺僌儔僼偼壗偲側偔埖偄偵偔偦偆側暤埻婥偑偁傞偑丄幚偼丄倣倧倓 乮俀値亄侾乯偱峫偊傞
偲丄
丂丂丂丂丂丂丂俥乮倠乯佭俀倠丂乮 倣倧倓 乮俀値亄侾乯 乯
偲偄偆扨弮側峔憿偵側偭偰偄傞偙偲偑暘偐傞丅乮仺嶲峫丗崌摨幃乯
丂偙偺偲偒丄丂丂俥倣乮倠乯佭俀倣丒倠丂乮 倣倧倓 乮俀値亄侾乯 乯丂偱偁傞丅
丂偙偙偱丄丂倣亖俀値丂偲偡傞偲丄丂俀倣亅侾亖乮俀値亅侾乯乮俀値亄侾乯丂傛傝丄
丂俀倣亅侾佭侽丂乮 倣倧倓 乮俀値亄侾乯 乯丂偡側傢偪丄丂俀倣佭侾丂乮 倣倧倓 乮俀値亄侾乯 乯偱偁傞丅
丂偟偨偑偭偰丄丂倣倧倓 乮俀値亄侾乯丂偵偍偄偰丄丂丂俥倣乮倠乯佭俀倣丒倠佭倠
丂丂丂傛偭偰丄丂俥倣乮倠乯亖倠丂偲側傞丅
丂埲忋偐傜丄丂俀値 枃偺僇乕僪傪丄俀値 夞僔儍僢僼儖偡傞偲丄昁偢尦偵栠傞丅
乮僐儊儞僩乯丂儕僼儖僔儍僢僼儖偼丄堦尒暋嶨偦偆側峔憿偲巚偄偒傗丄幚偼扨側傞乽俀攞乿偺峔憿
丂丂丂丂丂丂偲偄偆偙偲偱丄偦傫側偵暋嶨側僔儍僢僼儖偼弌棃側偄偲偄偆偙偲側偺偩傠偆丅偦傟偵
丂丂丂丂丂丂偟偰傕丄偙偺搶嫗戝妛偺栤戣傪嶌栤偝傟偨愭惗偺庯枴偺峀偝偵偼偨偩扙朮偡傞
丂丂丂丂丂丂偺傒偱偁傞丅
乮捛婰乯丂暯惉侾俋擭俈寧俀俀擔晅偗
丂偙偺僔儍僢僼儖傪擖帋栤戣偵偟偨偲偙傠偑懠偵傕偁偭偨丅
亙俀侽侽俈擭搙丂惞怱彈巕妛堾拞摍壢丂擖帋栤戣亜
丂侾偐傜侾侽傑偱偺悢帤偑傂偲偮偢偮彂偐傟偨僇乕僪偑丄偼偠傔恾嘥偺傛偆偵堦楍偵暲傋傜
傟偰偄傑偟偨丅恾嘥偺僇乕僪偺嵍懁俆枃偲塃懁偺俆枃傪岎屳偵暲傋丄恾嘦偺傛偆偵暲傋偐
偊傑偟偨丅
丂丂丂丂丂恾嘥丂丂侾丂丂俀丂丂俁丂丂係丂丂俆丂丂俇丂丂俈丂丂俉丂丂俋丂丂侾侽
丂丂丂丂丂恾嘦丂丂侾丂丂俇丂丂俀丂丂俈丂丂俁丂丂俉丂丂係丂丂俋丂丂俆丂丂侾侽
丂侾偲侾侽偺埵抲偼曄傢傝傑偣傫偑丄俀偐傜俋傑偱偺僇乕僪偼偡傋偰埵抲偑曄傢偭偰偄傑偡丅
摨偠暲傋偐偊傪偔傝曉偟峴偆偲偒丄師偺栤偄偵摎偊側偝偄丅
丂乮侾乯丂恾嘦偐傜丄傕偆侾夞暲傋偐偊傪峴偭偨偲偒丄偼偠傔偲摨偠埵抲偵栠傞僇乕僪偑偁傟偽丄
丂丂丂偦偺悢帤傪偡傋偰摎偊側偝偄丅乮侾偲侾侽偼彍偒傑偡丅乯
丂乮俀乯丂偡傋偰偺僇乕僪偑恾嘥偺暲傃曽偵偼偠傔偰栠傞偺偼丄偙偺暲傃偐偊傪壗夞峴偭偨
丂丂丂偲偒偱偡偐丅恾嘥偐傜偺夞悢傪摎偊側偝偄丅
丂乮俁乯丂恾嘥偐傜侾侽侽夞暲傃偐偊偨偲偒丄侾偺塃偳側傝偵偁傞僇乕僪偺悢帤偼偄偔偮偱偡偐丅
丂侾偲侾侽偺埵抲偼曄傢傜側偄偺偱丄寢嬊偼丄乽俀丄俁丄係丄俆丄俇丄俈丄俉丄俋乿偺儕僼儖僔儍僢僼儖
偺栤戣偱偁傞丅
丂搶嫗戝妛擖帋栤戣偺岞幃傪梡偄傟偽丄俀3 枃側偺偱丄俀亊俁亖俇 夞僔儍僢僼儖偡傞偲昁偢
尦偵栠傞丅
丂偟偐偟丄庴尡惗偼彫妛惗側偺偱丄偦偺傛偆側夝摎偼堘斀偱偟傚偆偹丠
丂恾嘥偐傜恾嘦偺暲傋偐偊傪惛嵏偡傞偲丄師偺傛偆側弰夞抲姺偺愊偱昞偝傟傞偙偲偵婥偑
偮偔丅
丂丂丂丂丂丂丂丂乮 俀丂俁丂俆丂俋丂俉丂俇 乯乮 係丂俈 乯
乮 係丂俈 乯偼屳姺側偺偱丄乮 係丂俈 乯乮 係丂俈 乯偼峆摍抲姺偲側傞丅
丂偙偺偙偲偐傜丄乮侾乯偺夝摎偼丄乽丂係丂偲丂俈丂乿偲側傞丅
傑偨丄弰夞抲姺 乮 俀丂俁丂俆丂俋丂俉丂俇 乯偼丄丂乮 俀丂俁丂俆丂俋丂俉丂俇 乯6丂偑峆摍抲姺偲側傞丅
傛偭偰丄丂乮俀乯偺夝摎偼丄乽丂俇夞丂乿偲側傞丅
乮俁乯偼丄乮俀乯傪梡偄偰夝寛偝傟傞丅丂侾侽侽亐俇亖侾俇丒丒丒係丂側偺偱丄
乮 俀丂俁丂俆丂俋丂俉丂俇 乯100乮 係丂俈 乯100亖乮 俀丂俁丂俆丂俋丂俉丂俇 乯4亖乮 俀丂俉丂俆 乯乮 俁丂俇丂俋 乯
偡側傢偪丄恾嘥偐傜丄侾侽侽夞偺憖嶌偱恾嘨偲側傞丅
丂丂丂丂丂恾嘨丂丂侾丂丂俆丂丂俋丂丂係丂丂俉丂丂俁丂丂俈丂丂俀丂丂俇丂丂侾侽
埲忋偐傜丄乮俁乯偺夝摎偼丄乽丂俆丂乿偲側傞丅
乮僐儊儞僩乯丂彫妛惗偵抲姺偺抦幆傪婜懸偡傞偙偲偼偱偒側偄偑丄抲姺傪梡偄側偔偰傕巻偲墧
丂丂丂丂丂丂昅偑偁傟偽夝摎傪摫偔偙偲偑弌棃傞偩傠偆丅偦傟偵偟偰傕丄偄偄栤戣偩両
乮捛婰乯丂暯惉俀侽擭侾侾寧俁擔晅偗
丂摉俫俹偺宖帵斅乽弌夛偄偺愹乿偵丄俧俙俬 偝傫偑偙偺僔儍僢僼儖偺榖戣偵嫽枴傪帩偨傟丄師
偺傛偆側昞傪姰惉偝傟偨丅宖帵斅偼帪偲嫟偵徚偊嫀傞塣柦側偺偱丄俧俙俬 偝傫偺寢壥傪偙偺
儁乕僕偵旛朰榐偲偟偰巆偟偨偄偲巚偆丅
丂俧俙俬 偝傫偺寢壥偐傜丄岞幃偺岆傝偵婥偯偒丄杮暥傪廋惓偝偣偰偄偨偩偒傑偟偨丅忋婰偼
廋惓嵪傒偱偡丅俧俙俬偝傫偵姶幱偄偨偟傑偡丅