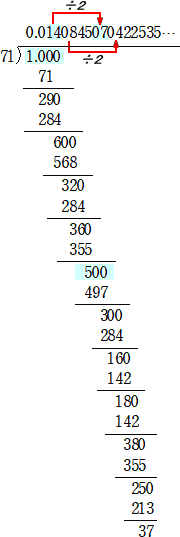当HPがいつもお世話になっているHN「GAI」さんが、循環節のある性質について考察さ
れた。(平成25年2月12日付け)
10を原始根に持っている法pで、1〜100までの素数を調べると、
p=7、17、19、23、29、47、59、61、97
の9個がある。これらに共通に言える性質として、
1/p を小数にしたとき、循環節の長さが p-1 (偶数)で、その循環節の
前半部分の数+後半部分の数=999…9 (9が (p-1)/2 個並ぶ)
となる。
例1 1/7=0.142857142857… から、循環節の前半=142、循環節の後半=857 より、
循環節の前半+循環節の後半=999
例2 1/17=0.05882352941176470588… から、
循環節の前半=05882352 、循環節の後半=94117647 より、
循環節の前半+循環節の後半=99999999
例3 1/97=0.01030927835051546391752577319587628865979381443298969
0721649484536082474226804123711340206185567010309…
循環節の前半=010309278350515463917525773195876288659793814432
循環節の後半=989690721649484536082474226804123711340206185567
循環節の前半+循環節の後半
=999999999999999999999999999999999999999999999999
これはこれで計算機等で確認できるんですが、これを、1〜1000 までの素数に広げると以
下
p=7、17、19、23、29、47、59、61、97、・・・、223、229、233、257、…、983
と素数7からカウントすると、52個存在していた。これらの素数に対しても同様な現象が起こ
るとは思われるが確認していくには切りがない。何方かこれを証明して頂けませんか?
上の性質は10を原始根とするときの現象であるなら、他の数の原始根である場合はどん
なことに繋がるのか?この辺りの知識に詳しい方は情報を下さい。
空舟さんからのコメントです。(平成25年2月12日付け)
111111は、7で割り切れます。(← 1が並ぶ数字の中では最小)
111111/111=1001は、7で割り切れます。(上記の仮定より、111は7と素だから)
よって、 1/7 + 1000/7 = 1001/7 は整数です。ここで、1000/7は、1/7の小数点を3つずら
したものです...と言う考察で理解することができます。
飯高先生の研究室の卒業研究論文に似た話題が有ったと思います。(あんまり読んでな
いのでどんな話か把握していないけれど)
当HP読者のHN「ILM」さんから、上記話題に関連してメールを頂いた。
(平成25年3月26日付け)
1/p を小数にしたとき、循環節の長さが p-1 (偶数)で、その循環節の
前半部分の数+後半部分の数=999…9 (9が (p-1)/2 個並ぶ)
について私なりの証明を思いつきました。以下書きたいと思います。
(証明) 10を原始根に持つ素数pに対して、1/pの循環節をa、長さをwとおくと、
1/p=a/10w+a/102w+……
となり、右辺を整理して、1/p=a/(10w−1) より、 10w−1=ap
上式の両辺を、mod p で見て、 10w−1≡0 (mod p)
さて、pの定義より、上式を満たす最小のwは、p−1 であるので、10p-1−1=ap ・・・(*)
a=b×10(p-1)/2+c (b、c≦10(p-1)/2−1) とおくと、(*)より、
10p-1−1=(b×10(p-1)/2+c)p なので、c=(10p-1−1)/p−b×10(p-1)/2 となる。
ところで、求めるものは、b+c であるから、
b+c=b+(10p-1−1)/p−b×10(p-1)/2=(10(p-1)/2−1)((10(p-1)/2+1)/p−b)
ここで、 (10(p-1)/2+1)/p は整数なので(もし割り切れなかったらpの定義に反する )、
(10(p-1)/2+1)/p=d とおいて、 b+c=(10(p-1)/2−1)(d−b) ・・・(*:*)
(10(p-1)/2+1)(10(p-1)/2−1)=(b×10(p-1)/2+c)p より、
pd(10(p-1)/2−1)=(b×10(p-1)/2+c)p
よって、 d(10(p-1)/2−1)=b×10(p-1)/2+c より、(d−b)10(p-1)/2=c+d ・・・(***)
(*:*)×10(p-1)/2 と(***)より、 (b+c)10(p-1)/2=(c+d)(10(p-1)/2−1)
ここで、10(p-1)/2−1 と 10(p-1)/2 は互いに素なので、10(p-1)/2−1 は、b+c を割り切る。
b、c の定義より、 b+c≦2×(10(p-1)/2−1) であるから、
b+c=10(p-1)/2−1、2×(10(p-1)/2−1)
であるが、b+c=2×(10(p-1)/2−1) のときは、b=c=10(p-1)/2−1 であり得ない。
以上より、 b+c=10(p-1)/2−1 なので、9 が (p-1)/2 個並ぶ事になる。 (証終)
(♯) もしかしたら間違いがあるかもしれませんが、こんな感じになりました。加えて、もし
p が原始根に10を持たなかったらどうなるかはまだ検討してないので、暇があったら
やってみたいと思います。
(コメント) ILMさん、証明ありがとうございます。自然な流れに感動しました!
ILMさんからの続報です。(平成25年3月28日付け)
ふと思ったんですが、循環節の長さw、即ち、法p(p は素数)における10の位数が偶数
であれば同様の証明が成り立ちますね。つまり、
10w≡1 (mod p) を満たす最小の自然数wが偶数のとき、
1/p の循環節の前半と後半を足すと、10w/2−1 となって、9がw/2 個並ぶ事になる
ということです。あとは10の位数が奇数のときを考察すればいいわけですが、難しそうです
ね。まず分割の仕方がわからない。何か閃いたらまたメールしたいと思います。
ILMさんからの続報です。(平成25年3月29日付け)
循環節について、さらに別のことを思いつきました。別に10進数表示でなくてもいいですよ
ね。つまり、さらに一般化して、
pを素数、qをpと互いに素な数として、qの位数w、即ち、qw≡1 (mod p) を満た
す最小の自然数 w が 1/p をq進数表示した時の循環節の長さとなり、さらに w が偶
数のとき、その循環節の前半と後半を足すと、qw/2−1 となって、q−1 が w/2 個並
ぶ事になる。
ということが同様に証明できますね。よく考えると、別に 1/p ではなく、r を p と互いに素な p
未満の数として r/p でもいいはずですが...。
あとはこれを応用すると、r/p のq進数表示を求めたければ、循環節の長さを求め、前半だ
け頑張って計算し、後半は前半を見て足した時に q-1 になるように埋めていけばいいことが
わかります。
具体的に、 1/7 の 3 進数表示を求めたければ、7 を法としたときの 3 の位数は 6 なので、
最初の三桁を頑張って求め、0.010……となったらあとはこれを見て、0.010212……と埋める、
ということです。
しかし、これは便利なんですかね? 手計算では手間が半減のような、位数を求めるのが面
倒のような、結局あまり変わらないのでは、という感じです。私はあまりq進数表示を求めるよ
うなことをしてこなかったので、あまりありがたみがわかりませんが、どうなのでしょうか。
(追記) 令和4年8月10日付け
1/7 の循環節の長さにも驚かされるが、循環節が長いものとして、1/71も有名だろう。
実際に、
1/71=0.01408450704225352112676056338028169
01408450704225352112676056338028169・・・
循環節は、35桁もあるが、最初の7桁を覚えれば、以降の数は機械的に得られるという
点も興味深い。
実際に割り算を実行してみると、そのカラクリが見えてくる。