当HPの掲示板「出会いの泉」に、当HPがいつもお世話になっているHN「at」さんが次の
ような問題を出題された。(平成24年9月13日付け)
問題 nを任意の正の整数とする。今、1 が 1個、2 が 2個、… 、n が n 個 あるも
のとする。これら n(n+1)/2 個の数のすべてを同じ数が隣り合わないように横一列
に並べる。このような並べ方の総数を a(n) 通りとするとき、a(100)の値はいくつに
なるか?
例 a(1)=1 、a(2)=1 、a(3)=10 、a(4)=1074 、a(5)=1637124 である。
実際に、例えば、n=3 のとき、32323 の隙間に1を入れる場合が6通り、
31323や32313の隙間に2を入れる場合が2通りずつあり、6+2+2=10(通り)となる。
この数列は、オンライン整数列大辞典(A190945)に、現在までのところ、n=13 までの値が
登録されている。
GAI さんからのコメントです。(平成24年9月14日付け)
およそ 5050!/(2!*3!*4!*・・・*100!)*(1/2)^97*(1/100) くらい?
at さんからのコメントです。(平成24年9月14日付け)
5050!/(2!*3!*4!*・・・*100!)*(1/2)^97*(1/100) は、9540桁の正整数になりますね。気が向
いたらa(100)の正確な値を求めてみてください。私が計算機を使って行った計算によると正
確な値は、9542桁の正整数になりました。(→参考:数式処理ソフトmaximaによる計算結果)
GAI さんからのコメントです。(平成24年9月14日付け)
at さんが出された数値を確認しました。(私はPARI/GPという計算ソフトを利用)もちろん、
これは近似値であり、その正確な値はわかりません。とりあえず、a(14)を正確に出すことに
挑戦できないでしょうか?どなたか、プログラムを組んで求めて頂きたいが...。
空舟さんからのコメントです。(平成24年9月15日付け)
i までの数字を使った並びで隣接が j 箇所ある並び方を二重配列a[i][j]に入れて、漸化式
的に求めてみました。
(a[1]=[1]、a[2]=[1,2]、a[3]=[10,26,18,6]、a[4]=[1074, 3366, 4170, 2730, 1020, 216, 24]、... と
なるように、a[i-1]を元にして、a[i]を計算していく方針です。)
配列が書きやすい(よく書き慣れてる)javascriptで実装しました。javascriptを知らなくてもや
ってることは分かりやすいと思います...。(C(x,y)は組合せ、H(x,y)は重複組合せ)
<script>
var N=20;var a=[[],[1]];
for(i=2;i<=N;i++){a[i]=[];var s=(i-1)*i/2+1; //s:i-1までを使った並びの数+1
for(j=0;j<s;j++){
y=0;
for(k=0;a[i-1][k];k++){ // a[i-1][k]からの寄与を考える。
var d=j-k; //差分
//隣接をm個除去しておいてd+m個隣接を増やす入れ方を考える。
//隣接箇所(k)からm箇所選んでに数字を入れ
//非隣接箇所(s-k)からmm=(i-d-2m)箇所数字を入れ
//入れた数字(m+mm)にd+m個数字を重複的に追加する方法の数である。
//mの範囲は0≦m≦k, かつ0≦mm≦s-k となる範囲、そしてm+mm≠0。
//dが負の時もあるから d+m<0 もはじく。
for(m=0;m<=k;m++){
if(d<0)m=-d;
var mm=i-d-2*m;
if(0<=mm && mm<=s-k && m+mm!=0){
y+=a[i-1][k]*C(k,m)*C(s-k,mm)*H(m+mm,d+m);
}}}
a[i][j]=y;
}}
</script>
※空舟さんからの補足(平成24年9月15日付け)
実際の所調べてみると、上記で、 mm≦s-j にしても mm≦s-k にしても、この条件は機能
していないらしく[恒等的]、不要のようです。(この条件をはずしても同じ結果になりました。)
検証:mm =i-m-(d+m)≦i 、s-k ≧i*(i-1)/2+1- (i-1)*(i-2)/2 ≧i より
s-k≧i≧mm が言える。s-j は、j≦k のときは、s-j≧s-k≧i≧mm でOK
j>k のときは、d=j-k>0 なので、s-j=(s-k)-d≧i-d≧i-m-(d+m)=mm
a[i][0] を、i = 1 から順番に出力したものは以下です。javascriptなので浮動小数点になっ
ていますが(+オーバーフロー)
a1 = 1
a2 = 1
a3 = 10
a4 = 1074
a5 = 1637124
a6 = 45156692400
a7 = 27230193578558160
a8 = 4.2029643494394156e+23
a9 = 1.9020007156743964e+32
a10 = 2.843464512159537e+42
a11 = 1.5621373884080024e+54
a12 = 3.4720858746642464e+67
a13 = 3.40830776138113e+82
a14 = 1.6016029459985872e+99
a15 = 3.881569719975021e+117
a16 = 5.200082108321898e+137
a17 = 4.10881703493172e+159
a18 = 2.0349827869217582e+183
a19 = Infinity
a20 = NaN
とりあえず合ってそうですね。実は私自身は数学ソフトでのプログラミングはよくできない
ので後は任せます。なお、漸化式を一応数式で書いておくと、
a[i][j]=ΣΣa[i-1][k]*C(k,m)*C(s-k,mm)*H(m+mm,d+m)
ここで、s=(i-1)*i/2+1, d=j-k, mm=i-d-2m
Σの範囲(kとmについての和)は、
・kはa[i-1][k]が存在する範囲、つまり、0≦k≦(i-1)*(i-2)/2
・mは0≦m≦k かつ d+m≧0 かつ 0≦mm≦s-j かつ m+mm≠0
GAI さんからのコメントです。(平成24年9月15日付け)
最初意味が分からず、書いてある通りに全パターンを書き出し(n=3で実行)、隣接する個
数をカウントすることで、まず下の行列の意味がわかりました。
(a[1]=[1]、a[2]=[1,2]、a[3]=[10,26,18,6]、a[4]=[1074, 3366, 4170, 2730, 1020, 216, 24]、... と
なるように、a[i-1]を元にして、a[i]を計算していく方針です。)
上の方針を実行していくときの着眼点も掴みきれず、とりあえず漸化式を、n=2 即ち、
a[2][0]=1、a[2][1]=2 のデータを基に、n=3での a[3][0]、a[3][1]、a[3][2]、a[3][3] を導いていく
と、なんとピッタシと現れてくるではありませんか!(よくこんな規則が裏に隠れていることに気
づけますね。ほんと感心します。しかもこれを記述する工夫も凄い!)空舟さんの漸化式の活
用を目指して、計算ソフトでプログラミング中です。
(私はプログラムは初心者で上手くいくかな???)
GAI さんからのコメントです。(平成24年9月15日付け)
空舟さんが示された漸化式で、
a[3][0]=10 、a[3][1]=26 、a[3][2]=18 、a[3][3]=6
より、 a[4][0]=1074 まで、私が解釈した漸化式で構成できることが確認できたのですが、
次の a[4][1] を出すときに行き詰まっています。どこがおかしいのかご指摘下さい。
a[4][1]=a[3][0]*C(0,0)*C(7,3)*H(3,1) + a[3][1]*C(1,0)*C(6,4)*H(4,0)
+ a[3][1]*C(1,1)*C(6,2)*H(3,1) + a[3][2]*C(2,1)*C(5,3)*H(4,0) + a[3][3]*C(3,2)*C(4,2)*H(4,0)
=10*1*35*3+26*1*15*1+26*1*15*3+18*2*10*1+6*3*6*1
=1050+390+1170+360+108 = 3078
空舟さんの結果 a[4][1]=3366 に対して -288(6の倍数分)不足してしまいました。
空舟さんからのコメントです。(平成24年9月15日付け)
k=2、m=2 と k=3、m=3 が抜けているようです。a[3][2]*C(2,2)*C(5,1)*H(3,1)=270、
a[3][3]*C(3,3)*C(4,0)*H(3,1)=18 を加えると合います。その次は、
a[5]=[1637124, 6175296, 10226280, 9877440, 6217680, 2686656, 815304, 174000, 25500,
2400, 120]
a[6]=[45156692400, 200052724080, 407307126240, 507210750480, 433434545880,
270058551840, 127142908200, 46217310480, 13130544240, 2929689840, 512302560,
69506640, 7161000, 537600, 27000, 720]
になっています。
GAI さんからのコメントです。(平成24年9月16日付け)
空舟さんによる漸化式の提示を受けて、例のオンライン整数列大辞典にも載っていない
n=14、15での正確な値を計算ソフトを利用して求めてみました。
なお、y(14,0)がa(14)に相当する値になります。(a(15)はy(15,0)になります。)
以下、y(14,n)の値は、同じものを含む105(=1+2+3+・・・+14)個の数字を並べたとき、隣に
同じ数字が並んでいる個数がn個である場合の総数になります。
a(14)=y(14,0)
=16016029459985875606798676171028758593081536344920890361863264740976338483
98824106722597980721984000
a(15)=y(15,0)
=38815697199750221664144803610305604011772332370822925627884508054754223508
59154139368271934640369126993346182798080000
その他の隣接数に対応する場合の数(→ 参考)
at さんからのコメントです。(平成24年9月16日付け)
私の計算によるa(14)の値は、GAIさんの示されたy(14,0)の値と完全に一致しています。私
の計算方法は包除原理を使ったもので、a(n)の値だけしか求めることができません。
(y(14,2)やy(14,3)に相当するものは私の計算方法ではわからないです。)
a(15)の値も、GAIさんの示された値で間違いないと思います。私の計算では、
a(20)
=154153662951163661668418347459109977994449840778947953198330393605739366550
668040729072970121940909926786637754163094125373800382845531577698229021548
964931460056137492675286412868495863955175997012028635074610101277336323498
755571712000
となりました。
GAI さんからのコメントです。(平成24年9月16日付け)
確認お願いします。
a(20)
=154153662951163661668418347459109977994449840778947953198330393605739366550
668040729072970121940909926786637754163094125373800382845531577698229021548
964931460056137492675286412868495863955175997012028635074610101277336323498
755571712000
a(19)
=669043210744269934985822296285360221293484591853878004479923362207956581549
752907442087829009749293812894046518507517232564805649441204113664299670920
99179554077993061569125421870640939911138667817003804672000
a(18)
=203498278692175899742743781329016894314300211471634571518233036784706985686
350451706495207916098321466536050134420682470953757763652978356820175238209
5460452410654971202564275410944000
a(17)
=410881703493172170945667552195140630805937876605368166920095283149010060772
418285374554760168320691838849273879311078051939654080357132449749170621093
9548160000
a(16)
=520008210832189859924214574823280144447190717474392949132171050029205084739
351946224138534275493208110511108703374340683743272007702579200
Seiichi Manyama さんからのコメントです。(平成28年1月3日付け)
Ruby による計算結果
(追記) 令和5年6月24日付け
いくつかの「数え上げ」の問題に挑戦しました。
問題 円周上に等間隔に並ぶ8個の点から3個選んで三角形を作る。回転や裏返しで重
なるものは同一と見ることにして、異なる三角形は何個出来るか?
(解) 隣り合う2点間の弧の長さを1とする。三角形の3辺 a、b、c に対応する弧の長さに
着目して、求める場合は、
(a,b,c)=(1,1,6)、(1,2,5)、(1,3,4)、(2,2,4)、(2,3,3)
の5通りである。 (終)
問題 立方体ABCD-EFGHの頂点Aから出発し、立方体の辺に沿って次々に隣の頂点
に進み、全部の頂点を1回ずつ通って最後の頂点に達する方法の数を求めよ。
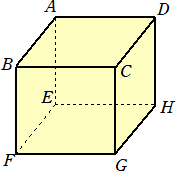
(解) Aを出発して次に行く頂点の可能性は、B、D、E の3通りあり、それぞれの場合の数
は同数であるので、「A→B」の場合を調べれば十分である。
・A→B→C→D の場合