
当HPがいつもお世話になっているHN「よおすけ」さんから話題を提供して頂きました。
(平成24年1月7日付け)
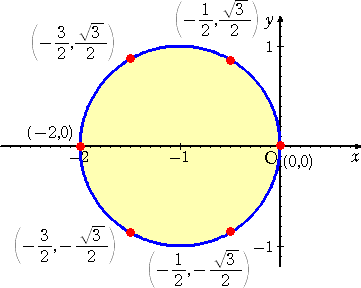
円 (x + 1)2 + y2 = 1 の周上に、(m+n/2,n
全部で何個あるか。
このような点全体の集合を正三角形格子という。
(m+n/2,n
(2m + n +2)2 + 3n2 = 4
(2m + n +2)2 = 4 - 3n2 ≧ 0 より、 n = 0 、1 、-1
n = 0 のとき、 (2m + 2)2 = 4 より、 2m + 2 = ±2 よって、 m = 0 、-2
n = 1 のとき、 (2m + 3)2 = 1 より、 2m + 3 = ±1 よって、 m = -1 、-2
n = -1 のとき、 (2m + 1)2 = 1 より、 2m + 1 = ±1 よって、 m = 0 、-1
以上から、求める点は全部で、6個ある。
同様の問題です。(平成24年1月10日付け)
円 (4x - 1)2 + (4y)2 = 72 の周上に、(m+n/2,n
点を全て求めよ。
攻略法さんからのコメントです。(平成24年1月11日付け)
解は、 (0,±
この問題に関連して、
素数 p≡1 (mod 4) に対して、X2+Y2=pk を満たすような整数の組 (X,Y) の
個数は、4(k+1) 個ある。
素数 p が、p≡1 (mod 4)、pk≡1 (mod 8) を満たすとき、
円 (4x - 1)2 + (4y)2 = pkの周上には、ちょうど k+1 個の格子点がある。
素数 p≡1 (mod 4) に対して、円 (2x-1)2+(2y)2=pk の周上には、2k+2 個
の格子点がある。
(追記) 平成24年1月11日付け
出典は、2011/10/30の第213回数学検定準1級2次:数理技能検定の問題5(選択)の改題
です。僕も受けましたが、他の問題で苦戦したうえ、全くやりませんでした。でも、後になって
やってみると・・・良い問題です。