
当HPがいつもお世話になっているHN「FN」さんより韓国の「大学修学能力試験」の話題
をいただいた。(平成22年11月25日付け)
1週間前の11月18日に、韓国で大学修学能力試験が実施された。人口は半分以下の
はずだが、志願者が70万人強というから、日本のセンター試験よりはかなり多い。
数学は、30問を100分で解く。そのうち、21問は5択で、残りの9問が短答式(3桁以内
の自然数を答える)となっている
数学には一部記述式での解答があるというようなことが書いてあったが、記述式があっ
たのは2005年までのようである。論理的に不正確であっても答が合えばいいとなれば、
それほど時間をかけなくてもできるかもしれない。
カ型とナ型があって、カ型が理型、ナ型が文型のようである。因みに、カナダラ・・は英語
のABC・・、日本語のアイウ・・(イロハ・・)に相当するので、A型、B型のようなものである。
カ型は、25問は共通問題で残り5問を微分積分・確率統計・離散数学から選択する。
ごく易しい問題もあるが、結構難しい問題もある。日本のセンター試験より難しいかなと
いう気がする。
センター試験は1つの問題に何個かの設問があるが、韓国の方は30問すべて独立の
問題で、1問1答形式である。下記にカ型の問題がある。
http://www.seoul.co.kr/SAT/2011/2/Math_odd_ga.pdf
1は、式だけでわかる。
2は、A(A+B)のすべての成分の和を求めよ。
3は、PA=2PB となるときの a を求めよ。
(ここまではごく容易)
4は、すべての実根の積を求めよ。
5になるとかなり難しくなる。
Pは楕円上の点で直線PAが円と交わる点のうちAでない方の点をQとする。Pが楕円上
を動くとき、Qが動く範囲の長さを求めよ。
6以下韓国語を読むのが難しい(韓国語初心者にとって)問題がかなりある。問題の意味
が取れたなかで難しいのは次の2問。
24 最高次の係数が1で、f(0)=3、f’(3)<0である4次関数 f(x) がある。実数 t に対し
て、集合Sを、S={ a|関数|f(x)− t|がx=aで微分可能でない}とする。集合Sの
要素の個数を、g(t) とする。関数 g(t) が、t=3と t=19でだけ不連続であるとき、
f(−2)の値を求めよ。
25 自然数mに対して、大きさが同じ立方体を1列目に1個、2列目に2個、3列目に3個、
・・・、m列目にm個積む。立方体の個数が偶数である列に対して次の操作をする。
立方体の個数を半分にする。偶数であればさらに半分にする。立方体の個数が奇
数になるまで繰り返す。
すべての列について、この操作が終わった後の1列目からm列目までの立方体の個
数の和を、f(m)とする。このとき、
とするとき、p+q の値を求めよ。ただし、pとqは互いに素な自然数。
どちらも記述式の問題として、30分ぐらいは考えられる状況で出題すべき問題のように思
う。100分で30問だから、1問平均3分強、このあたりの問題でも、10分ほどしかかけられ
ないでしょう。
(コメント) 量にも圧倒されますが日本のような柔な問題とは異なる質の高さを感じますね!
平均点や最高点がどの程度なのか気になるところです。FNさんに感謝します。
当HPがいつもお世話になっているHN「攻略法」さんが、25番の問題を解かれた。
(平成22年11月27日付け)
(略解) 計算メモ
1,┃2,┃3,4,┃5,6,7,8,┃9,10,11,12,13,14,15,16,┃17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,┃…
1,┃1,┃3,1,┃5,3,7,1,┃9, 5,11, 3,13, 7,15, 1,┃17, 9,19, 5,21,11,23, 3,25,13,27, 7,29,15,31, 1,┃…
1 4 16 64(項数2=82より) 256
※f(2n+2)を順に求めることになるが、「奇数の和(=平方数)」で計算は容易になる。
より、
n f(2n) f(2n+1) f(2n+2)
0: 1 2 6
1: 2 6 22
2: 6 22 86
3: 22 86 342
4: 86 342 1366
となる。数列 { f(2n+2) }={ 6,22,86,342,1366,… }の階差数列が、
16,64,256,1024,…
より一般項は、 6+16(4n−1)/3=(4n+2+2)/3 (n=0,1,2,・・・)
また、数列 { f(2n+1)−f(2n) }={ 1,4,16,64,256,… }の一般項は、4n なので、
したがって、 p+q=3+16=19 (終)
(別解) 入試は直感!!?
表から、 f(2n+1)=4f(2n)−2 となる。これより、 f(2n+2)=16f(2n)−10 となる。
したがって、 f(2n) → ∞ なので、 p/q=3/16 が直ちに分かる。
よって、 p+q=19
(コメント) n=0,1,2,・・・ の様子を調べて、問題の一般的構造を把握する方法は、
日本でいうと、難関大学の2次試験レベルの問題と言えますね!
FNさんからのコメントです。(平成22年11月27日付け)
攻略法さんの解答のように具体的に考えれば、分子が 4n はすぐわかり、分母も等比数
列の和で出るので、あるいは10分ぐらいでできるのかもしれません。
FNさんが、上記の24を次のように改題された。(平成23年2月10日付け)
24’ 最高次の係数が1で、f(0)=3、f’(3)<0である4次関数 f(x) がある。f(x)の極値が
3と19だけであるとき、f(−2)の値を求めよ。
24では、微分可能とか不連続とか、この問題にとって本質的でない言葉を使ってわざと
難しく見せています。受験生でこのページを見てる人がいれば挑戦してみてください。大学
修学能力試験で要求されるのは結果だけですが、きちんと記述式で書いてください。
そうですか〜、「本質的でない言葉を使ってわざと難しく見せている」んですか...。確か
に、上記のような分かり易い表現だと、取り組んでみようという気になりますね!
実際に解いてみました。
(解) 最高次の係数が1で、f(0)=3、f’(3)<0である4次関数 f(x) の極値が3と19だけで
あるので、極値を与える x の値は、α、β、γ (α<β<γ)の3つあり、f’(3)<0 よ
り、α=0 であることが分かる。さらに、 f(β)=19 、f(γ)=3 が成り立つ。
このとき、 f’(x)=4x(x−β)(x−γ)=4x3−4(β+γ)x2+4βγx より、
f(x)=x4−(4/3)(β+γ)x3+2βγx2+3 と書けるので、
f(β)=β4−(4/3)(β+γ)β3+2β3γ+3=−(1/3)β4+(2/3)β3γ+3
より、 −(1/3)β4+(2/3)β3γ+3=19 すなわち、 β4−2β3γ+48=0
f(γ)=γ4−(4/3)(β+γ)γ3+2βγ3+3=−(1/3)γ4+(2/3)βγ3+3
より、 −(1/3)γ4+(2/3)βγ3+3=3 すなわち、 γ4−2βγ3=0
γ≠0 なので、 γ=2β これを、 β4−2β3γ+48=0 に代入して、
β4=16 となる。 β>0 なので、 β=2 よって、 γ=4
以上から、
f(−2)=16−8・(−8)+16・4+3=16+64+64+3=147 (終)
(補足) 例えば、 f(x)=x4−8x3+16x2+3 とすると、
f’(x)=4x3−24x2+32x=4x(x−2)(x−4)
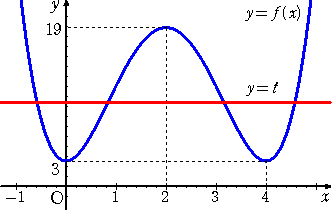
上図からも分かるように、
関数 g(t) (関数|f(x)− t|がx=aで微分可能でないときのaの個数)
の値は、t=3、t=19 以外の、ある t の近傍では、 0 または 2 または 4 の何れか
の定数で連続であるが、
t=3 の近傍では、0 ←→ 4 、 t=19 の近傍では、2 ←→ 4
と不連続に変化する。
したがって、問題24の意味するところは、問題24’と同等になるわけだ。
(コメント) なるほど...納得!! FNさんに感謝します。
FNさんからのコメントです。(平成23年2月12日付け)
単に想像ですが、韓国では上記のような問題は何回か出題されていて、多少ひねった形
での出題しかできないような状況なのかなと思います。あくまでも想像です。
私の解答を書いておきます。
(解) 最高次の係数が正である4次関数は次のどちらかである。
(1) 極大値 1つと極小値 2つを持つ。
(2) 極小値 1つを持つ。
題意から、考える場合は、(1)で、2つの極小値が一致するしかない。
このとき、極大値が19で、極小値が3となる。
f(0)=3 より、極小値3を与える x の1つは、0である。もう1つの x の値を p とする。
f(x)−3は、x=0、p で極小値0をもち、最高次の係数が1だから、
f(x)−3=x2(x−p)2 すなわち、 f(x)=x2(x−p)2+3 と書ける。
このとき、 f’(x)=2x・(x−p)2+x2・2(x−p)=2x・(x−p)(2x−p)
従って、x=p/2 のとき、f(x) は極大となる。
よって、f(p/2)=p4/16+3=19 より、 p4=162=44 なので、 p=±4
p=−4 のとき、 f’(3)=6・7・10=420>0 となり、条件「f’(3)<0」に反する。
従って、p=4 で、 f(x)=x2(x−4)2+3 であることから、
f(−2)=4・36+3=147 である。 (終)
極小値を与える x の1つがわかってる場合でしたが、極大値を与える x がわかってる場
合を類題として書いておきます。この場合は、「f’(3)<0」に相当する式はなくても、f(x)は確
定します。
24” 最高次の係数が1で、f(1)=2である4次関数 f(x) がある。f(x) の極値が、2と−14
だけであるとき、f(5)の値を求めよ。
大学修学能力試験では、答は3桁以内の整数なので、f(5)としましたが、普通は、「f(x) を
求めよ」でいいです。
(コメント) FNさんの解答で、「f(x)−3=x2(x−p)2」と置いているところが受験テクニックで
すね!スッキリした解法で清々しいです。
24”の答えは、「130」かな? f(x) は、f(x)=(x−3)2(x+1)2−14 となります。