
当HPの掲示板「出会いの泉」(平成22年8月17日付け)で、HN「凡人」さんが次の問題
を提起された。
正n角形の対角線の本数は、n(n−3)/2 で求められるが、正n角形の対角線の
交点の個数は、n の式で表すことができるだろうか?
凡人さんは、図を描くことで、次の表を得られた。
正n角形の対角線の交点 
当HPの掲示板「出会いの泉」(平成22年8月17日付け)で、HN「凡人」さんが次の問題
を提起された。
正n角形の対角線の本数は、n(n−3)/2 で求められるが、正n角形の対角線の
交点の個数は、n の式で表すことができるだろうか?
凡人さんは、図を描くことで、次の表を得られた。
| n | 3 | 4 | 5 | 6 | 7 | 8 |
| 個数 | 0 | 1 | 5 | 13 | 35 | 49 |
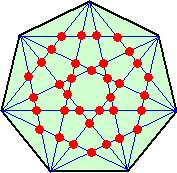
正7角形の対角線の交点
正7角形の場合、7つの頂点から4つ選び四角形を作ると、その対角線の交点が一つ決
まることから、7C4=35(個)となる事が分かる。
また、正6角形で同様に計算すると、 6C4=15(個)だが、中心で3本の対角線が1点で
交わっていることから、3回数えており、余計な2回を引かなければならない。
よって、正6角形の対角線の交点の個数は、15−2=13(個)となることが分かる。
ところで、この2回というのは、 3C2−1 で計算することができる。
このことから、正6角形の対角線の交点の個数は、 6C4−3C2+1 と表すことができる。
同様の考えで、正8角形では、 8C4−21 で求めることができると予想した。
再び図を見ると、
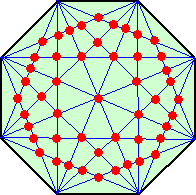
3本の対角線が1点で交わる点が8個、4本の対角線が1点で交わる点が1個あり、
(3C2−1)×8+(4C2−1)×1=21
が求められる。
そこで、凡人さんは、以上の計算をもとに、一般に、
正奇数角形の場合は、nC4(個)
正偶数角形の場合は、nC4−Σ[k=3〜?]{(kC2−1)・ak}
のような形で書けるのではないかと予想された。
凡人さんは、現在、次の問題点を研究中とのこと。
・正奇数角形であれば、3本の対角線が1点で交わることが無いのか?
・ak は具体的に求めることができるのか?
この問題について、当HPがいつもお世話になっているHN「らすかる」さんによれば、
「正奇数角形のとき、3本の対角線が1点で交わることはない」
とのことです。(平成22年8月18日付け)
さらに、当HPがいつもお世話になっているHN「FN」さんからご教示いただきました。
(平成22年8月18日付け)
下記の論文で完全に解かれているとのこと。
http://arxiv.org/PS_cache/math/pdf/9508/9508209v3.pdf
2006年の論文ですが、完全な式が与えられたのは初めてだと書いてあります。しかし、
1936年に本質的に解かれていたらしいです。計算ミスがあって完全ではなかった。
この1936年の結果は気付かない人が多くて、1958年に次の問題が出された。
n が素数のとき、正n角形の3本の対角線が1点で交わることはないことを示せ。
これに対して、素数の場合が1961年に、奇数の場合が1962年に解かれたそうです。
即ち、凡人さんの1つ目の問いは、1962年(実際には、1936年?)に解かれているようで
す。
(コメント) 凡人さん、らすかるさん、FNさん、ありがとうございます。FNさんが紹介された論
文によれば、
正n角形の対角線の交点の個数は、
nC4+ (−5n3+45n2−70n+24)/24・δ2(n)−(3n/2)・δ4(n)
+(−45n2+262n)/6・δ6(n)+42n・δ12(n)+60n・δ18(n)
+35n・δ24(n)−38n・δ30(n)−82n・δ42(n)−330n・δ60(n)
−144n・δ84(n)−96n・δ90(n)−144n・δ120(n)−96n・δ210(n)
ただし、n≡0 (mod m) のとき、δm(n)=1 で、その他の場合は、δm(n)=0
で与えられるとのことなので、具体的に計算してみました。
例 n=8 のとき、すなわち、正八角形のとき、
8C4+ (−5・83+45・82−70・8+24)/24・δ2(8)−12・δ4(8)
+(−45・82+262・8)/6・δ6(8)+42・8・δ12(8) +60・8・δ18(8)
+35・8・δ24(8)−38・8・δ30(8)−82・8・δ42(8)−330・8・δ60(8)
−144・8・δ84(8)−96・8・δ90(8)−144・8・δ120(8)−96・8・δ210(8)
=8C4+ (−5・83+45・82−70・8+24)/24・1−12・1
+(−45・82+262・8)/6・0+42・8・0+60・8・0
+35・8・0−38・8・0−82・8・0−330・8・0
−144・8・0−96・8・0−144・8・0−96・8・0
=70+(−2560+2880−560+24)/24−12
=70−9−12
=49
となり、冒頭の表の結果と一致する。(う〜む、なるほど!)
(コメント) ひょんなことから、正n角形の対角線の交点数を知る必要があり、いろいろ考察
してみた。(令和6年8月9日付け)
n が奇数のときは、対角線の交点数の計算は、単純に、 nC4 で求められる。
例 正五角形の対角線の交点は5個である。これは、計算で、 5C4=5 で求められる。

例 正七角形の対角線の交点は35個である。これは、計算で、 7C4=35 で求められる。

n が偶数のときは、奇数のときと違って、一般に求めるのは難しい。
例 正方形の対角線の交点は1個である。これは、四角形に対して、その対角線の交点は、
ただ1個であることを示す。

例 正六角形の対角線の交点は、6C4=15 としたいところだが、この中には、3本の対角線
が1点で交わる場合が含まれており、重複して数えられているので、調整が必要である。

計算では、 6C4−3+1=15−2=13(個) となる。
例 正八角形の場合

3本の対角線が1点で交わる点が8個、4本の対角線が1点で交わる点が1個あるので、
求める対角線の交点の個数は、
8C4−8×(3−1)−1×(6−1)=70−16−5=49(個)
次の表が知られている。
| n | 4 | 6 | 8 | 10 | 12 | 14 |
| 個数 | 1 | 13 | 49 | 161 | 301 | 757 |