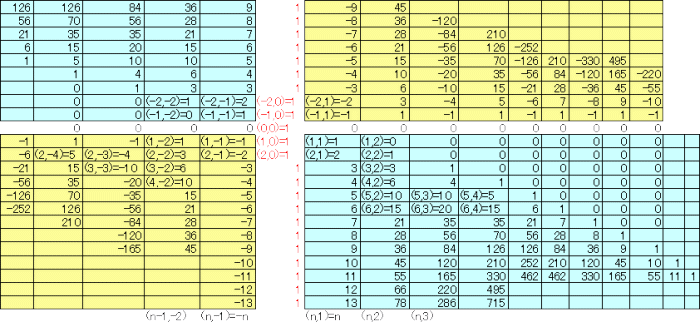
当HPの読者のK.S.さんより、平成24年9月9日付けで標記話題をメールで頂いた。
パスカルの三角形は平面全体へ拡張することができる。
「数学する精神」(加藤文元 著 中公新書)にあった内容(半平面への拡張)を踏まえ、全
平面への拡張を考察してみました。
通常、2項係数 nCr は、n>0、r>0 のとき、
nCr=n(n−1)(n−2)・・・(n−r+1)/r!
と定義されている。 r>n ならば、nCr=0 とすると、
(1+x)n=1+nC1x+nC2x2+・・・+nCnxn+nCn+1xn+1+・・・
と級数の形に表すことができる。次に、n<0 のときも、
(1+x)n=1+nC1x+nC2x2+・・・+nCnxn+nCn+1xn+1+・・・
としてよい。実際に、 1/(1−x)n+1=Σk=0〜∞ n+kCkxk (n≧0) が成り立つことは、
1/(1−x)n+1 の第k次導関数(k≧1)が
(n+1)(n+2)・・・(n+k)(1−x)-n-k-1=k!n+kCk(1−x)-n-k-1
であることから、Taylor の定理より明らかだろう。このことから、
1/(1−x)n+1=Σk=0〜∞ {(-n-1)(-n-2)・・・(-n-k)}/k!・(-x)k
なので、敢えて、負の自然数 k に対して、
k!=(−k)(−k−1)・・・(−2)(−1)
と考えて、 {(-n-1)(-n-2)・・・(-n-k)}/k!=-n-1Ck と2項係数を拡張すれば、
1/(1−x)n+1=Σk=0〜∞ -n-1Ck・(-x)k
すなわち、 1/(1+x)n=Σk=0〜∞ -nCk・xk
と書けることが分かる。このとき、n<0 に対して、
(1+x)n=1/(1+x)-n=Σk=0〜∞ nCk・xk
と級数の形に表すことができる。−1<x<1 で意味を持ち、テイラー展開となる。
n>0、r<0 や n<0、r<0 のときも同様に、 r!=(−r)(−r+1)・・・(−2)(−1)
とすれば、平面上原点を中心に対称な値を持つように定義されると思う。そのとき、級数的に
どのような意味を持つでしょうか?