
自然対数の底eが持つ最も優れた、そして最も美しい性質は、
という微分の公式だろう。この性質のおかげで計算公式が大変簡略化される。この性質は、
とも言い換えることができる。従って、
となる a の値を、eと定義する場合もある。しかし、本来のeは、このような美しい形で世に
登場したわけではない。
eについては、ネーピア(John Napier)の1594年から1614年までの20年間の労作
Mirifici logarithmorum canonis descriptio 「素敵な対数表の解説」
を抜きに語ることは出来ない。
彼が生きた時代16〜17世紀は、あらゆる分野で科学が進展した時代であった。コペルニ
クスの地動説が受け入れられ、新しい宇宙観のもと、ケプラーは惑星の3つの運動法則を発
見、また、マゼランの地球一周航海が成功(1521年)し、メルカトールによる新しい世界地図
の発明(1569年)は航海術に大きな影響を与えた。これらの発展に伴って、科学者に数値計
算の重労働が課せられることになった。コンピュータなどない時代なので、紙と鉛筆で地道に
計算するほかなかった。(加法と減法しか出来ないが、17世紀半ばにパスカルは計算機を考
案している。ただし、計算の効率は悪かったらしい。)
時代は、この退屈な重労働から科学者たちを解放するような発明を待っていた。この発明に
立ち向かったのがネーピアであった。残念ながら、ネーピアがどのような着想で対数の発明に
到達したのかは不明である。しかし、それを類推することは可能だ。彼は、三角法には精通し
ていたので、当然、加法定理による積和の公式は知っていただろう。この公式は、三角比の
積の計算を、和の計算に置き換える働きを持つ。同じように、幾何数列に対して、算術数列が
対応すること(つまり、公比を r として、r の2乗と r の4乗を掛ける場合、指数の和2+4=6
を求めて、r の6乗とするに等しい)も知っていただろう。(1829年エコールポリテクニクの口
頭試問で、エヴァリスト・ガロアが不合格となった、いわくつきの問題である!)
このように、積の世界を和の世界に導くものとして、ネーピアは対数という着想を得たのでは
ないだろうか。
ネーピアは、ある1つの数Xを定めて、任意の数Nを N = Xn と表すようにしたかったらしい。
もし、これが出来れば、
M = Xm 、 N = Xn のとき、M × N = Xm+n 、 M ÷ N = Xm-n
となるからである。
問題は、Xの値として何が適当かということであった。例えば、X=2 だと、幾何数列は、
1,2,4,8,・・・となり、値が飛び飛びになって隙間があきすぎてしまう。
そこでネーピアは、Xとして十分小さな数を選べば、累乗がゆっくり変化していくのではと考え
た。しかし、あまり小さすぎると、累乗の変化の仕方が遅すぎてしまう。ネーピアは、1に近いが
近すぎない数として、X=0.9999999とした。つまり、X=1−(10の−7乗)である。このXを
用いて幾何数列を計算するわけであるが、ネーピアはさらに、なるべく小数の計算を使わない
ように工夫した。その当時、小数は既に知られていたが、まだ一般の人は使い慣れていなかっ
たからである。そこで、数列の各項に10の7乗を掛けることにしたのである。このことにより、
小数計算から解放されることになった。
10の7乗 =10,000,000
(10の7乗)×(X) = 9,999,999
(10の7乗)×(Xの2乗) = 9,999,998
(10の7乗)×(Xの3乗) = 9,999,997
・・・・・・・・・・・・・・・・・・
(10の7乗)×(Xの100乗)= 9,999,900
N=(10の7乗)×(XのL乗)と書くとき、Lは
Nのネーピアの対数(logarithm=比logos+数arithmos)
いわれる。
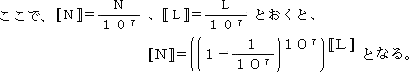
このとき我々は、現代風の e の定義:
を思い出す。
即ち、ネーピアの対数は、現代風にいえば、底を1/eとする対数を意味する。