最短経路問題　　　　　　　　　　　　　　　　　　　　　　　

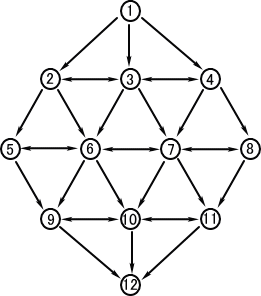
番号１を出発して、矢印の向きに従って、番号 　１２へ到達する方法について考える。 　 　　順列・組合せの理論から簡単に分かるように、 　逆戻りしないという条件で、その道順の数は、全 　部で３２４通りある。 　 　　実際に、３×６×６×３＝３２４　である。 　　しかし、この問題設定は、あまり現実的ではない。 　通常、移動する経路によって、移動に要する時間 　は異なるはずだからである。 　 　このような問題設定において、番号１を出発して、 矢印の向きに従って、番号１２へ到達する道順のう ち所要時間が最短の経路を求める手順を考えたい。

　今、下図のように各経路毎に所要時間が決まっているものとする。

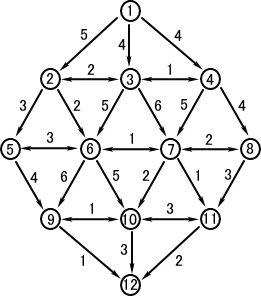まず、番号ｍから番号１２に移動する最短時間を、 ｈ(ｍ）で表す。明らかに、次が成り立つ。 　　　　ｈ(ｍ)＝ｍｉｎ（ｆ(ｍ，ｎ)＋ｈ(ｎ）） 　　但し、ｆ(ｍ，ｎ)は番号ｍから番号ｎに移動するの 　に要する時間であり、ｍｉｎは、番号ｍから移動可 　能な番号 ｎ を動かしたときの最小値を考えるもの 　とする。 　　求めたい値は、ｈ(１)であるが、ゴールから逆算、 　すなわち、ｈ(１２)から順次求めていくことにより、 　問題は解決される。以下にその計算を示す。

ｈ(１２)＝０

ｈ(１１)＝ｍｉｎ（ｆ(１１，１２)＋ｈ(１２)、ｆ(１１，１０)＋ｈ(１０)）＝ｍｉｎ（２、３＋ｈ(１０)）

ｈ(１０)＝ｍｉｎ（ｆ(１０，９)＋ｈ(９)、ｆ(１０，１２)＋ｈ(１２)、ｆ(１０，１１)＋ｈ(１１)
　　　＝ｍｉｎ（１＋ｈ(９）、３、５、６＋ｈ(１０)）＝ｍｉｎ（１＋ｈ(９）、３）

ｈ(９)＝ｍｉｎ（ｆ(９，１２)＋ｈ(１２)、ｆ(９，１０)＋ｈ(１０)）＝ｍｉｎ（１、１＋ｈ(１０)）＝１
　　　よって、ｈ(１０)＝２、ｈ(１１)＝２

ｈ(８)＝ｍｉｎ（ｆ(８，１１)＋ｈ(１１)、ｆ(８，７)＋ｈ(７)）＝ｍｉｎ（５、２＋ｈ(７)）

ｈ(７)＝ｍｉｎ（ｆ(７，６)＋ｈ(６)、ｆ(７，１０)＋ｈ(１０)、ｆ(７，１１)＋ｈ(１１)、ｆ(７，８)＋ｈ(８)）
　　　＝ｍｉｎ（１＋ｈ(６)、４、３、７、４＋ｈ(７)）＝ｍｉｎ（１＋ｈ(６)、３）

ｈ(６)＝ｍｉｎ（ｆ(６，５)＋ｈ(５)、ｆ(６，９)＋ｈ(９)、ｆ(６，１０)＋ｈ(１０)、ｆ(６，７)＋ｈ(７)）
　　　＝ｍｉｎ（３＋ｈ(５)、７、７、２＋ｈ(６)、４）＝ｍｉｎ（３＋ｈ(５)、４）

ｈ(５)＝ｍｉｎ（ｆ(５，９)＋ｈ(９)、ｆ(５，６)＋ｈ(６)）＝ｍｉｎ（５、６＋ｈ(５)、７）＝５
　　　よって、ｈ(６)＝４、ｈ（７)＝３、ｈ(８)＝５

ｈ(４)＝ｍｉｎ（ｆ(４，３)＋ｈ(３)、ｆ(４，７)＋ｈ(７)、ｆ(４，８)＋ｈ(８)）
　　＝ｍｉｎ（１＋ｈ(３)、８、９）＝ｍｉｎ（１＋ｈ(３)、８）

ｈ(３)＝ｍｉｎ（ｆ(３，２)＋ｈ(２)、ｆ(３，６)＋ｈ(６)、ｆ(３，７)＋ｈ(７)、ｆ(３，４)＋ｈ(４)）
　　　＝ｍｉｎ（２＋ｈ(２)、９、９、２＋ｈ(３)、９）＝ｍｉｎ（２＋ｈ(２)、９）

ｈ(２)＝ｍｉｎ（ｆ(２，５)＋ｈ(５)、ｆ(２，６)＋ｈ(６)、ｆ(２，３)＋ｈ(３)）＝ｍｉｎ（８、６、４＋ｈ(２)、１１）＝６
　　　よって、ｈ(３)＝８、ｈ(４)＝８

ｈ(１)＝ｍｉｎ（ｆ(１，２)＋ｈ(２)、ｆ(１，３)＋ｈ(３)、ｆ(１，４)＋ｈ(４)）＝ｍｉｎ（１１、１２、１２）＝１１

　以上から、所要時間が最短な道順は次の通りである。

　　　　　　　　　番号１⇒番号２⇒番号６⇒番号７⇒番号１１⇒番号１２

　例題程度だと、目算で最短経路を見つけることもできる。しかし、上記計算の優れている所
は、あらゆるダイヤグラムに対して、有効な一般的方法であるということである。多少計算は
長いが、その実、計算は全く機械的であり、易しい。

(参考文献：木下栄蔵　著　好奇心の数学（電気書院））