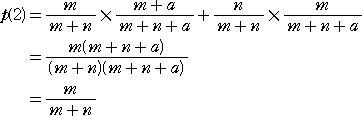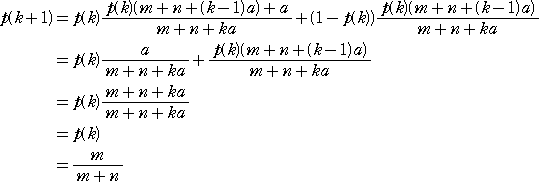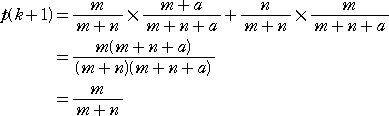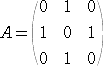数理化学

数理化学　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　物理数学というと、学生時代に物理学科の講義を受講した記憶が蘇るが、数理化学とい
う名前は、一般には馴染みが薄いかもしれない。

　大学の物理は数学に、大学の数学は哲学になるとよく言われるが、大学の化学にも、面
白い数学の問題が潜んでいるらしい。

　このページでは、細矢治夫先生（お茶の水女子大学名誉教授）から伺った話題について
整理しようと思う。

　グラフ理論や組合せ理論が２０世紀に急速に進歩したが、その一因として、ハンガリーの
数学者　ポリア（　1887-1985）の業績（１９３６年）があげられる。ポリアから遡る
こと２００年前の１７３６年は、オイラー（Ｅｕｌｅｒ）がケ－ニヒスベルグの橋の問題をグラフ理
論的に解決した年でもある。その意味で、１７３６年は、グラフ理論の誕生の年と言われる。
ただ、その後の２００年間、ポリアが現れるまでほとんどグラフ理論の進展はなかったとい
う。

　ポリアは、炭化水素の異性体を系統的に数え上げるために、置換群という新しい方法論
を確立したことで有名である。異性体という化学の話題が、数学の理論を使えば機械的に
求められる。ここら辺からが、歴史的に、数学と化学のコラボレーションの始まりと言えるの
だろうか？

　さらに、「ポリア」というと、次の「ポリアの壷（Polya's urn）の問題」も有名だろう。

　 ポリアの壷の問題

　　　壷の中に赤玉がｍ個、黒玉がｎ個が入っている。無作為に１個取り出し色を見て
　　壺の中に戻す。その際、取り出した玉の色と同色の玉をａ個新たに加えるものとする。
　　　このとき、ｋ回目の試行で赤玉を取りだす確率は、ｋによらず一定で、

　　　　　　　

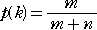
　　で与えられる。

　　（コメント）　新たに加える玉の個数ａの値が、０ならば、上記は反復試行なので結果
　　　　　　　　は当然だろう。ａの値が、１以上でも成り立つというところが面白い。

　　　　まず、

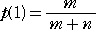　は明らかである。

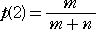　であることも簡単に示される。

　　　　すなわち、２回目の試行で赤玉を取り出すということは、

　　　　　　１回目に赤玉、２回目も赤玉　または　１回目に黒玉、２回目は赤玉

　　　　という２つの場合に分けられるので、求める確率は、

　　　　　

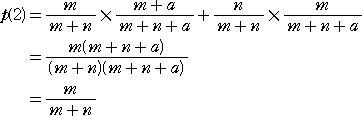
　　　計算過程を眺めていると、ｋの任意の値に対して、いつも成り立つような．．．予感は
　　するが、厳密には、数学的帰納法により示される。

　　　（略証）　ｋ＝１のときは明らか。いま、

　　　　　　　　　　　　　　

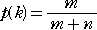
　　　　が成り立つと仮定する。ｋ回目の試行のときに壺の中に入っている玉の総数は、

　　　　ｍ＋ｎ＋（ｋ－１）ａ個で、その中から赤玉を取り出す確率がｐ（ｋ）ということから、

　　　　その中には、赤玉が推定で、ｐ（ｋ）｛ｍ＋ｎ＋（ｋ－１）ａ｝個入っていたことになる。

　　　　もちろん、黒玉の個数は、推定で、｛１－ｐ（ｋ）｝｛ｍ＋ｎ＋（ｋ－１）ａ｝個である。

　　　　このとき、

　　　

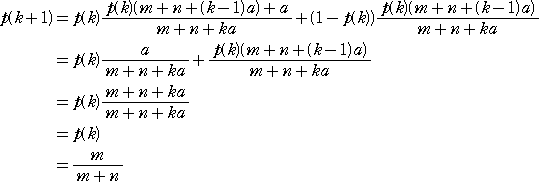
　　　　となり、命題は、ｋ＋１のときも成り立つ。

　　　　　よって、すべてのｋに対して、

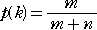　　　　　　　　　　　　　　　　　　（略証終）

　　　（コメント）　ｋ回目の試行のときに、壺の中の玉の個数を推定していますが、なぜか
　　　　　　　　　整数値でないところが少し不安ですね！一応雰囲気が合っていれば、ＯＫ
　　　　　　　　　ということで．．．。

　　　（追記）　平成２０年１２月２９日付け

　　　　　　上記の証明で、玉の個数を推定するということを行っていて少し不安であったが、
　　　　　ＨＮ「凡人」さんから、推定しなくても次のように考えればよいというアドバイスを頂い
　　　　　た。（２８日付け）

　　　　　　ｋ－１回目の試行が終わったときに壷の中に赤玉がｍ個、黒玉がｎ個が入っ
　　　　　ているものとする。

　　　　　　このとき、ｋ＋１回目の試行で赤玉を取り出すということは、

　　　　　　　ｋ回目に赤玉、ｋ＋１回目も赤玉　または　k 回目に黒玉、ｋ＋１回目は赤玉

　　　　　という２つの場合に分けられるので、求める確率は、

　　　　　　　　　

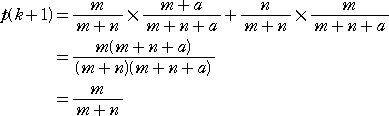
　　　　　（コメント）　こちらの証明の方がスッキリしますね！「凡人」さんに感謝します。
　　　　　　　　　　　上記の数学的帰納法の記述も修正すれば、Ｏ．Ｋ．（牧場）かな？

　さて、話を数理化学の話題に戻そう。

　高校の化学の授業で、

　ＣＨ₄（メタン）　、　Ｃ₂Ｈ₆（エタン）　、　Ｃ₃Ｈ₈（プロパン）　、　Ｃ₄Ｈ₁₀（ブタン）　、

　Ｃ₅Ｈ₁₂（ペンタン）　、　Ｃ₆Ｈ₁₄（ヘキサン）　、　Ｃ₇Ｈ₁₆（ヘプタン）　、

　Ｃ₈Ｈ₁₈（オクタン）　、　Ｃ₉Ｈ₂₀（ノナン）　、　Ｃ₁₀Ｈ₂₂（デカン）　、　・・・

と諳んじていた頃が懐かしい。これらは、　Ｃ_ｎＨ_2ｎ＋2 と一般的に表される炭化水素で、
特に、２重結合も環ももたない炭素間の単結合のみからなることから、アルカン（ａｌｋａｎｅ）
と命名されている。

　炭化水素には他にエチレン Ｃ₂Ｈ₄ のように、２重結合を１つ持つアルケン（ａｌｋｅｎｅ）や
アセチレン Ｃ₂Ｈ₂ のように、３重結合を１つ持つアルキン（ａｌｋｙｎｅ）がある。

　炭素原子と水素原子の原子価が、それぞれ４と１であることから、その構造を簡単に
図示することが出来る。

　たとえば、　プロパン Ｃ₃Ｈ₈ は、

　　　　　　　　　　　　　　　　　　　　　　

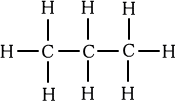
という構造になっている。ここで、炭素原子を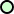で表し、炭素原子間だけの結合を－で
表すことにすれば、このプロパンの構造は簡単に、

　　　　　　　　

と略記される。左側から順番に番号を付ける。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　このとき、「１」は、「２」と隣接していて「３」とは隣接していない。また、「２」は「１」「３」の両
方に隣接している。「３」は、「２」と隣接していて「１」とは隣接していない。

　自分自身とは隣接していないものと考える。

　いま、行列Ａ＝（ａ_ｉｊ）を考え、その成分を次のように定める。

　　　「ｉ」と「ｊ」が隣接していれば、　ａ_ｉｊ＝１

　　　「ｉ」と「ｊ」が隣接していなければ、　ａ_ｉｊ＝０

　したがって、プロパンに対しては、次の３次の正方行列Ａが対応する。

　　　　　　　

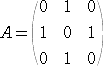
この行列は、隣接行列と呼ばれる。

　アルカンでは、ｎ＝３までは異性体は存在しないが、ｎ≧４のときは、異性体が存在する。

　たとえば、ｎ＝４　のときは、
　　　　　　　　　　　　　　　　

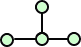
という２つの異性体が存在する。前者は「ｎ-ブタン」、後者は「２-メチルプロパン」または「イ
ソブタン」と呼ばれる。

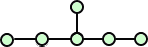
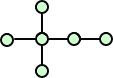
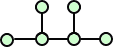
　さらに、ペンタン　Ｃ₅Ｈ₁₂　は、３つの異性体
　　　　　　　　　　　　　　

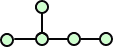
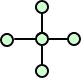
ヘキサン　Ｃ₆Ｈ₁₄　は、５つの異性体を有する。

　　　　　　　　

　　　　　　　　

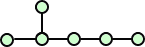
　一般に、Ｃ_ｎＨ_2ｎ＋2 の異性体の個数は次の表の通りである。