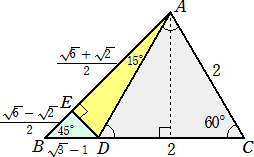２年半前、数学感動秘話の「数学十種競技」が好評だったみたいなので、僕から第２弾で
す。

　cos15°の値はいくらか。

※15°の代わりにπ/12ラジアン表記で答えてもかまいません。ただし、異なる２角α、βを
　用いたα-βの余弦の加法定理を用いた解法については、複数挙げてもかまいませんが、
　それのみのパターンを10通り、・・・という乱用は極力避けるようお願いします。

――という高校数学のド定番の問題を異なる方法で求めてください。

＃　高校範囲の数学だけでもかなりのやり方があるので、高校生の方の挑戦歓迎。


　らすかるさんが挑戦されました。（平成３０年４月８日付け）

　似たようなものが多いですが、とりあえず思い付いたものを書きます。

（方法１）・・・正弦の加法定理の利用

cos15°=sin75°=sin(30°+45°)=sin30°cos45°+cos30°sin45°
　　　　=(1/2)(1/√2)+(√3/2)(1/√2)=(√3+1)/(2√2)=(√6+√2)/4

（方法２）・・・余弦の加法定理の利用

cos15°=-cos165°=-cos(120°+45°)=sin120°sin45°-cos120°cos45°
　　　　=(√3/2)(1/√2)+(1/2)(1/√2)=(√3+1)/(2√2)=(√6+√2)/4

（方法３）・・・半角の定理＋二重根号の利用

cos15°=√{(1+cos30°)/2}=√{(1+√3/2)/2}=√(8+4√3)/4=(√6+√2)/4

（方法４）・・・直角三角形＋三平方の定理＋二重根号の利用

　AB=1、∠B=90°、∠C=15°の直角三角形ABCで、∠DAB=60°となるようにBC上に点D
をとると、BD=(√3)AB=√3、AD=2AB=2

∠DAC=15°から、CD=AD なので、CD=2

　よって、BC=BD+CD=2+√3、AC=√{1+(2+√3)^2}=√(8+4√3)=√6+√2　なので、

　cos15°=BC/AC=(2+√3)/(√6+√2)=(2+√3)(√6-√2)/4=(√6+√2)/4

（方法５）・・・二等辺三角形＋直角二等辺三角形＋正三角形の利用

　頂角A=30°、BC=2の二等辺三角形の内部に、斜辺がBCの直角二等辺三角形DBCを作
り、BDの延長とACの交点をEとすると、

　BD=CD=2/√2=√2、∠DCE=30°なので、CE=(2/√3)CD=2√2/√3=2√6/3、
　DE=(1/2)CE=√6/3

　AE=BE=BD+DE=√2+√6/3　より、AC=AE+CE=√6+√2

　また、△ABCの内部に正三角形FBCを作り、BCの中点をGとすると、

　FG=√3、AF=BF=2　なので、AG=2+√3

　よって、　cos15°=AG/AC=(2+√3)/(√6+√2)=(√6+√2)/4

（方法６）・・・正方形＋正三角形＋三平方の定理＋二重根号の利用

　一辺が 2 の正方形ABCDの内部に正三角形EBCを作り、ADの中点をFとすると、

　　AF=1、EF=2-√3　から、　AE=√{1+(2-√3)}^2=√(8-4√3)=√6-√2

　よって、　cos15°=AF/AE=1/(√6-√2)=(√6+√2)/4

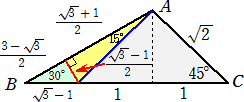
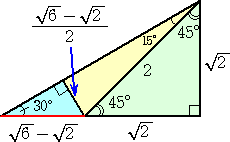
（方法７）・・・三角形の面積の公式利用

　∠B=60°、∠C=90°、AB=2 の直角三角形ABCに、CD=AC の直角二等辺三角形ACDが
接しているとき、

　　BC=1、CD=AC=√3、AD=(√2)AC=√6

　△ABDの面積は、BD×AC÷2=(BC+CD)×AC÷2=(1+√3)√3/2=(3+√3)/2

　三角形の面積の公式により、　AB・AD・sin∠DAB/2=(√6)sin75°=(3+√3)/2

　よって、cos15°=sin75°={(3+√3)/2}/√6=(√6+√2)/4

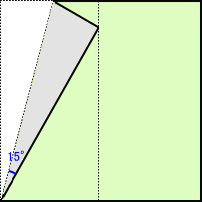
（方法８）・・・正方形＋正三角形＋tan＋二重根号の利用

　一辺が2の正方形ABCDの外側に正三角形EADをくっつけて、BCの中点をMとすると、

　tan15°=BM/EM=1/(2+√3)=2-√3

　ここで、　(tan15°)^2+1=1/(cos15°)^2 から、1/(cos15°)^2=(2-√3)^2+1=8-4√3

　よって、　cos15°=1/√(8-4√3)=1/(√6-√2)=(√6+√2)/4

（方法９）・・・座標平面の利用

　原点をOとするxy平面上において、A(√3+1,0)、B(√3+1,√3+1)とすると、△OABは、

　OA=AB=√3+1の直角二等辺三角形なので、OB=√6+√2

　C(2,2√3)、D(0,2√3)とすると、△OCDは∠C=60°、∠D=90°の直角三角形なので、

　OC=4

　直線OBの式は、y=x、直線BCの式は、y=-x+2+2√3なので、OBとBCは直交し、△OBCは

∠O=15°の直角三角形となる。

　よって、　cos15°=OB/OC=(√6+√2)/4

（方法１０）・・・三角形の辺の比の利用（よおすけ氏）

　三角形ＡＢＣにおいて、BC＝１＋、CA＝２、∠C＝６０°のとき、次の図が得られる。

左図より、 　　　　cos１５°＝｛（＋）/２｝/２ 　　　　　　　　　＝（＋）/４

（方法１１）・・・三角形の辺の比の利用（よおすけ氏）

　三角形ＡＢＣにおいて、BC＝1＋、CA＝、∠C＝45°のとき、次の図が得られる。

左図より、 　　 　cos15°={(+1)/2}/=（＋）/４

（方法１２）・・・単位円の利用（Ｓ（Ｈ）氏）

　単位円周上の２点Ａ（１，０）とＢ（/２，１/２）を結ぶ線分の中点Ｍ（（２＋）/４，１/４）

と原点を通る直線の方程式は、　ｙ＝（２−）ｘ　である。このとき、直線 ｘ＝１ との交点は、

（１，２−）なので、　ｔａｎ１５°＝２−　これより、　cos１５°＝（＋）/４

（方法１３）・・・２等分線の利用（Ｓ．Ｈ氏）

　ａ＝　、ｃ＝２　、∠Ｂ＝３０°、∠Ｃ＝９０°の直角三角形ＡＢＣにおいて、∠Ｂの２等分

線が辺ＣＡと交わる点をＤとおく。このとき、角の２等分線の性質から、Ｄは、辺ＣＡを、

：２に内分する点である。よって、　ＣＤ＝/（２＋）＝（２−）

　よって、　ｔａｎ１５°＝ＣＤ/ＢＣ＝２−

　これより、　cos１５°＝（＋）/４

（方法１４）・・・半円の利用（DD++氏）

　線分 AB を直径とする半径 の半円周上に、∠CAB=60°, ∠DAB=15° となるように
２点 C、D を取り、線分 CB と線分 AD との交点を E とする。線分 AB、BD、DA の長さを求
めることにより 15° の三角比が求められる。

※半径 なのは分数計算が出ないようにするだけの目的。半径 1/2 でやると BD と DA
　に直接 sin15° と cos15° が出てきます。

　まず、AB は直径なので、　AB＝２

　△ACB は直角三角形で、　AC＝　、CB＝

　△ACE は直角二等辺三角形なので、　CE＝　、AE＝２

　よって、　EB＝CB−CE＝−

　△DEB も直角二等辺三角形なので、　DE＝DB＝−１

　よって、　AD＝AE＋DE＝＋１

　したがって、ｓｉｎ１５°＝（−１）/（２）＝（−）/４

　　　　　　ｃｏｓ１５°＝（＋１）/（２）＝（＋）/４

　　　　　　ｔａｎ１５°＝（−１）/（＋１）＝２−

（方法１５）・・・三角形の辺の比の利用（Ｓ．Ｈ氏）

左図とにらめっこをすると自ずから、 　　　　　　ｃｏｓ１５°＝（＋）/４

（方法１６）・・・方程式の利用（スモークマン氏）

　らすかる様の他?の解法を考えてみました...。

　cos15°=x　、sin15°=y　（0<y<x）　とおくと、

　(x+y)^2-2xy=1　より、　(x+y)^2=1+1/2=3/2　から、　x+y=√6/2

　同様に、　(x-y)^2+2xy=1　より、　(x-y)^2=1/2　から、x-y=√2/2

　よって、　x=(√6+√2)/4

（方法１７）・・・方程式の利用（スモークマン氏）

　（方法１６）とほとんど同じですが...一応 ^^、複素数の回転で...。
(三角関数の2倍角と同じですけど...)

(cos15°+i*sin15°)^2=cos30°+i*sin30°で、cos15°=x　、sin15°=y　（0<y<x）　とおくと、

　(x+i*y)^2=(x^2-y^2)+i*(2xy)　なので、　x^2-y^2=√3/2　、　x^2+y^2=1

　これより、　2x^2=1+√3/2　から、　x^2=(2+√3)/4

　よって、　x=√(2+√3)/2  =(√2+√6)/4

（方法１８）・・・折り紙の利用

　次のように折り紙を２回折るだけで、１５°を作ることができる。

　　　　　　　　　

　この図を用いると、　ｔａｎ１５°＝（４−２）/２＝２−　であることは明らかだろう。

　このことから、　cos１５°＝（＋）/４　が求められる。


　　以下、工事中！