――という高校数学のド定番の問題、もちろん答えは「５」なわけですが、これを異なる１０通
りの方法で求めてください。
＃ 高校範囲の数学だけでもかなりのやり方があるので、高校生の方の挑戦歓迎。
（参考） 「最大と最小」
（コメント） 面白そうなので、挑戦してみました。（平成２７年１０月１８日付け）
（方法１）・・・不等式の利用
コーシー・シュワルツの不等式より、 （ｘ2＋ｙ2）（２2＋１2）≧（２ｘ＋ｙ）2 なので、
２５≧（２ｘ＋ｙ）2 から、 ２ｘ＋ｙ の最大値は、５
（方法２）・・・判別式の利用
２ｘ＋ｙ＝ｋ とおき、ｘ2＋ｙ2＝５ に代入して整理すると、 ５ｘ2−４ｋｘ＋ｋ2ー５＝０
この２次方程式が正の解α、βを持つので、
判別式 Ｄ/４＝４ｋ2−５ｋ2＋２５＝−ｋ2＋２５≧０ より、 −５≦ｋ≦５
α＋β＝４ｋ/５＞０ より、 ｋ＞０
αβ＝（ｋ2ー５）/５＞０ より、 ｋ＜−
、＜ｋ以上から、ｋの取り得る値の範囲は、
＜ｋ≦５ なので、最大値は、５（方法３）・・・点と直線の距離の利用
円 ｘ2＋ｙ2＝５ の中心（０，０）と直線 ２ｘ＋ｙ＝ｋ の距離は、 ｜ｋ｜/
最大になるのは、 ｋ/
＝ すなわち、 ｋ＝５ のときである。（方法４）・・・面積の利用
２ｘ＋ｙ が最大になるのは、円 ｘ2＋ｙ2＝５ と直線 ２ｘ＋ｙ＝ｋ （ｋ＞０）が接するとき。
面積を求めて、 ｋ2/４＝
・ｋ/４ より、 ｋ2＝５ｋ から、 ｋ＝５（方法５）・・・三角関数の利用
ｘ2＋ｙ2＝５ より、 ｘ＝
ｃｏｓθ、ｙ＝ｓｉｎθ とおける。このとき、 ２ｘ＋ｙ＝２
ｃｏｓθ＋ｓｉｎθ＝５ｓｉｎ（θ＋α）≦５ （ｔａｎα＝１/２）よって、最大値は、５
（方法６）・・・極値の利用
ｘ2＋ｙ2＝５ より、 ｘ＝
ｃｏｓθ、ｙ＝ｓｉｎθ とおける。このとき、 Ｙ＝２ｘ＋ｙ＝２
ｃｏｓθ＋ｓｉｎθＹ’＝−２
ｓｉｎθ＋ｃｏｓθ＝０ とおくと、ｔａｎα＝１/２ となるα（０＜α＜π/４）の前後で、Ｙ’＞０から Ｙ’＜０と変化するので、θ＝αのとき、Ｙは極大かつ最大である。
このときの最大値は、 ２
（２/）＋（１/）＝５ である。（方法７）・・・微分の利用
Ｙ＝２ｘ＋√（５−ｘ2） より、 Ｙ’＝２−ｘ/√（５−ｘ2）
Ｙ’＝０ とすると、ｘ＝２ で、その前後で、Ｙ’＞０から Ｙ’＜０と変化するので、ｘ＝２ のとき、
Ｙは極大かつ最大である。よって、最大値は、５ である。
（方法８）・・・ラグランジュの乗数の利用
Ｇ（ ｘ ， ｙ ）＝ｘ2＋ｙ2−５＝０ のとき、Ｆ（ ｘ ， ｙ ）＝２ｘ＋ｙ の極値を与える点（ ａ ， ｂ ）
は次の式を満たす。 ｘ2＋ｙ2−５＝０ 、２ｘ＋２λ＝０ 、２ｙ＋λ＝０
よって、 λ2＋λ2/４−５＝０ より、λ＝±２
条件より、ｘ＞０、ｙ＞０ なので、λ＜０ となり、 λ＝−２
このとき、 （ ｘ ， ｙ ）＝（ ２ ，１ ） が極値を与える候補である。
幾何学的に考えて、（ ２ ，１ ）において、２ｘ＋ｙ は極大かつ最大で、最大値は、５。
（方法９）・・・接線の方程式の利用
円 ｘ2＋ｙ2＝５ 上の接点（ｓ，ｔ）における接線の方程式は、ｓｘ＋ｔｙ＝５
これが、直線 ２ｘ＋ｙ＝ｋ と等しいので、ｓ＝２、ｔ＝１、ｋ＝５
よって、最大値は、５
（方法１０）・・・恒等式の利用（平成２７年１０月１８日付けで空舟さんよりご教示頂きました。）
（２ｘ＋ｙ）2＋（ｘ−２ｙ）2＝５（ｘ2＋ｙ2）＝２５ より、 （２ｘ＋ｙ）2≦２５ なので、
２ｘ＋ｙ の最大値は、５
（コメント） そろそろネタ切れかな？出題者のDD++さんは１１種類の解答を用意されている
とのこと。他に何があるかな？
さらに、探究してみました。
（方法１１）・・・ベクトルのなす角の利用
ベクトル（２，１）とベクトル（ｘ，ｙ） （ただし、ｘ2＋ｙ2＝５）のなす角をθとすると、
内積は、２ｘ＋ｙ で、大きさはともに
なので、 ｃｏｓθ＝（２ｘ＋ｙ）/５−1≦ｃｏｓθ≦１ なので、 ２ｘ＋ｙ≦５
よって、最大値は、５
（方法１２）・・・陰関数の微分の利用
ｘ2＋ｙ2＝５ の両辺をｘで微分すると、 ２ｘ＋２ｙｙ’＝０ よって、ｙ’＝−ｘ/ｙ
２ｘ＋ｙ が最大になるのは、直線 ２ｘ＋ｙ＝ｋ が円 ｘ2＋ｙ2＝５ に接するとき。
すなわち、−ｘ/ｙ＝−２ より、 ｘ＝２ｙ
ｘ2＋ｙ2＝５ に代入して、 ｘ＝２、ｙ＝１
よって、２ｘ＋ｙ の最大値は、 ２ｘ＋ｙ＝４＋１＝５ である。
（方法１３）・・・媒介変数表示の利用
（平成２７年１０月２０日付けで、Ｓ（Ｈ）さんよりご教示頂きました。）
媒介変数 ｔ を用いて、円 ｘ2＋ｙ2＝５ は、
ｘ＝
（１−ｔ2）/（１＋ｔ2）、ｙ＝２ｔ/（１＋ｔ2）と書ける。このとき、 ２ｘ＋ｙ＝２
（−ｔ2＋ｔ＋１）/（１＋ｔ2） となる。Ｙ＝（−ｔ2＋ｔ＋１）/（１＋ｔ2） とおくと、 Ｙ’＝（−ｔ2−４ｔ＋１）/（１＋ｔ2）
Ｙ’＝０ より、 ｔ＝−２±
ｔ＝−２＋
のとき、Ｙは極大かつ最大である。このとき、 Ｙ＝５ｔ/（−４ｔ＋２）＝５（−２＋
）/（１０−４）＝/２ なので、２ｘ＋ｙ＝２
・（/２）＝５ が最大値となる。（コメント） 数式処理ソフトを使えば何でもない計算かもしれないが、手計算ではあまりした
くない計算ですね！
（方法１４）・・・複素数平面の利用
（平成２７年１０月２０日付けで、３１５６さんよりご教示頂きました。）
ｚ＝ｘ＋ｙｉ、α＝２−ｉ とおくと、 ｚα＝（ｘ＋ｙｉ）（２−ｉ）＝２ｘ＋ｙ＋ｉ（２ｙ−ｘ） より、
Ｒｅ（ｚα）＝２ｘ＋ｙ
ここで、 ｜ｚ｜＝｜α｜＝
より、 Ｒｅ（ｚα）≦｜ｚα｜＝５ なので、２ｘ＋ｙ≦５ よって、最大値は、５
（コメント） なるほど！複素数を利用する手がありましたね。３１５６さんに感謝します。
（方法１５）・・・複素数の利用（方法１０とほぼ同じかな？）
ｘ2＋ｙ2＝５ より、 （ｘ＋ｙｉ）（ｘ−ｙｉ）＝（２＋ｉ）（２−ｉ）＝５
両辺に、２−ｉ を掛けて、
（ｘ＋ｙｉ）（２−ｉ）（ｘ−ｙｉ）＝（２ｘ＋ｙ＋ｉ（−ｘ＋２ｙ））（ｘ−ｙｉ）＝（２＋ｉ）（２−ｉ）2
両辺に、２＋ｉ を掛けて、
（ｘ＋ｙｉ）（２−ｉ）（ｘ−ｙｉ）（２＋ｉ）＝（２ｘ＋ｙ−ｉ（ｘ−２ｙ））（２ｘ＋ｙ＋ｉ（ｘ−２ｙ））
＝（２＋ｉ）2（２−ｉ）2＝２５
よって、 （２ｘ＋ｙ）2＋（ｘ−２ｙ）2＝２５ より、 ２ｘ＋ｙ≦５
よって、最大値は、５
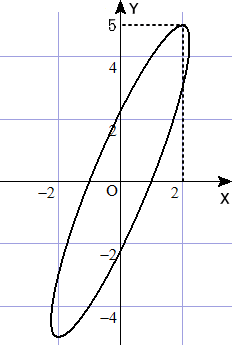
（方法１６）・・・楕円の利用
（平成２７年１０月２０日付けで、Ｓ（Ｈ）さんよりご教示頂きました。）
ｘ2＋ｙ2＝５ より、 ｙ＝√（５−ｘ2） なので、 Ｙ＝２ｘ＋ｙ＝２ｘ＋√（５−ｘ2）
Ｘ＝ｘ とおいて、点（Ｘ，Ｙ）の変化を調べる。２式より、ｘ を消去して、
Ｙ＝２Ｘ＋√（５−Ｘ2） から、 ５Ｘ2−４ＸＹ＋Ｙ2＝５
