す。
任意の三角形に対して、外側に正方形を作り、正方形の角どうしを結んで出来る三つの三
角形は、元の三角形と面積が同じ。
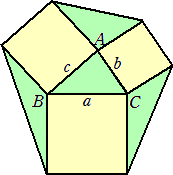
タイトルのような図形は、他にご存知でないしょうか?、
GAI さんからのコメントです。(平成28年11月17日付け)
この元の三角形ABCの3辺の長さを a、b、c (a<b<c) とすると、出来る三つの三角形を
それぞれ平行移動させ一つに合体させると、3辺の長さが、
√(2(a2+b2)-c2) 、√(2(b2+c2)-a2) 、√(2(c2+a2)-b2)
である、元の△ABCの3倍の面積となる三角形が出来ることになるんですね。
この3辺がすべて整数となれる(a,b,c)の組合せを調べてみました。(→ 一覧)
また、異形で同じ体積をもつ図形として有名なものとしては、カバリエリの原理による、
半径が r の半球
=半径 r、高さ r の円柱から中に半径 r、高さ r の円錐を逆さにしたものを彫り抜いた立体
(これより球の体積が4/3*π*r^3が導出可能)。
らすかるさんからのコメントです。(平成28年11月17日付け)
球の表面積(=4πr2)は、その球に外接する円柱の側面積(=2πr*2r=4πr2)と同じ
ですね。
ksさんからのコメントです。(平成28年11月17日付け)
皆さんありがとうございます。立体の表面積は意外でした。カバリエリの原理から、放物線
と直線の囲まれた面積は、放物線から直線を引いた新たな放物線とx軸で囲まれた面積に
等しい。
きっかけとなったのは、
「正方形の中に、一辺を半径とする四分円を描き、その中に、一辺を直径とする円を描くと、
二つの領域の面積が等しく、異形」
「正方形の中に一辺を直径とする半円を隣り合うようにかくとき、二つに囲まれた図形と隣
り合う辺の間にある頂点を中心に正方形の一辺を半径とする扇形をかき、そこから半円の
二つを引いた残りの部分が等積になる」
カルピスさんからのコメントです。(平成28年11月17日付け)
「はと目返し」する前の形と、した後の形 もいいかな?
「どんな四角形でも「はと目返し」をすると平行四辺形になる」で良かったかな?
ksさんからのコメントです。(平成28年11月18日付け)
カルピスさんありがとうございます。必殺、鳩目返し、任意の図形に対して成り立つ。パズ
ル王の中村先生の命名。
名前のことは知りませんでした。三角形でも、いろいろあるみたいですね。「図形の分割」と
して、既に出ていました。つまらない例ですが、
「正方形の一辺と対角線から、同心円を描くと、中の円とドーナツ部分が等しい」
あと、
「x軸とy軸とで囲む、4分の1の扇をかきます。さらに30度と60度の扇型の点をP,Qとす
る。P,Qから、y軸に垂線を下し、その足をそれぞれ、R,S,OQとPSの交点をTとする。
三角形OPTと四角形QRSTは同面積」
四角形を2等分すると、だいたい、四角形と三角形に二分されますね。珍しくもないですね。
#もともと同じ面積であれば、二つの図形を重ねて残りの部分は形は異なっても面積は同じ
になる。意外と当たり前なのがわかりました。
カルピスさんからのコメントです。(平成28年11月18日付け)
私は「忍法はと目返し」と呼んでいます。
「正方形の一辺と対角線から、同心円を描くと、中の円とドーナツ部分が等しい」
半径の比が「白銀比」の時、ドーナツとアンコが等しいのですね。これは、正方形において、
内接円の2倍が外接円になるのですね。
昔から「タングラム」という遊びがありますが、どんな形に変身しても面積は同じ...。清少
納言のタングラム、有名ですね...。
