構成された道があり、原点S(0,0)を始点、格子点G(5,5)を終点とする。

以下の各条件を満たすように、SからGへ移動するとき、それぞれ何通りの道順が存在す
るか?
(1)遠回りをせずに行く方法は?
(2)抜け道(遠回りは許されるが一度通った交差点や道は二度と通れない)の総数?
(3)領域 y>x への進入は禁止(y=x上の交差点は通行可能)された場合?
(4)すべての格子点を巡って、再びSへ戻ってくるハミルトン路(二度と同じ交差点、道は通れ
ない)の総数?
以下、上記の道の他に、直線 y=x+4、y=x+3、y=x+2、y=x+1、y=x、y=x-1、y=x-2、y=x-3、
y=x-4 なる新たな道が増設されたものとする。
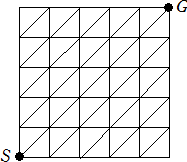
(5)上(北へ進む)、右(東へ進む)、斜め(北東へ進む)だけの進み方をとって進む場合?
(6)斜めに進めるためには、直前は右に移動している必要がある場合?
(7)領域 y>x への進入は禁止される場合?
(8)領域 y≧x への進入は禁止される(ただし、y=x 上の格子点は許される)場合?
(9)東西に走るすべての道には新たにバイパス道が新設され2本から一つを選んで進める
場合?
(10)北東に走るすべての道には新たにバイパス道が新設され2本から一つを選んで進める
場合?(ただし、(9)の条件は取り消したものとする。)
(コメント) なかなか難解なものばかりですね!分かる範囲で考えると、
(1) 10C5=252(通り)
(2) 組合せ爆発の問題で、求めるのは非常に大変です!答えは、1,262,816通り
(3) カタラン数 C5=10C4/5=42(通り)
