問題を考えていて思いついたのですが、次のような命題が成立しそうな予感がします。

　平面上に２点A、Bを取る。AP：PBが一定の比（1：1でない）になるような点Pの軌跡、すなわ
ち、アポロニウスの円をC₁とする。2点A、Bを通る任意の円C₂を描き、C₁との交点それぞれ
でC₂の接線を描くと、これらの接線の交わる位置は、円C₂の選び方によらず一定である。

……本当かな？


（コメント）　面白そうだったので、図を描いてみました。（平成２７年８月１８日付け）


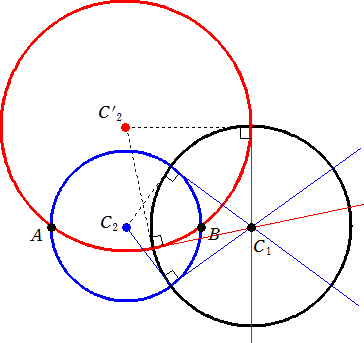
　　確かに、接線の交わる位置は、
　円C₂の選び方によらず一定っぽい
　ですね！

　　証明は、どうやるのだろう？

　　DD++さんが解答を書かれる前に、
　少し考えてみた。













　Ａ（ａ，０）、Ｂ（ｂ，０）とし、線分ＡＢをｍ：ｎ（ｍ＞ｎ）に内分する点Ｃ（（ｎａ＋ｍｂ）/（ｍ＋ｎ），０）、

ｍ：ｎに外分する点Ｄ（−ｎａ＋ｍｂ）/（ｍ−ｎ），０）で、線分ＣＤを直径とする円がアポロニウス

の円である。その中心の座標Ｃ₁は、（（−ｎ²ａ＋ｍ²ｂ）/（ｍ²−ｎ²），０）となる。

　今、円Ｃ₂の中心の座標を、（（ａ＋ｂ）/２，０）とすると、２円Ｃ₁、Ｃ₂の交点のｘ座標は、

　ｘ＝（ｎ²ａ＋ｍ²ｂ）/（ｍ²＋ｎ²）となる。

＃この一連の結果は面白いですね！中心の座標Ｃ₁は、線分ＡＢをｍ²：ｎ²に外分する点、
　２円Ｃ₁、Ｃ₂の交点のｘ座標は、線分ＡＢをｍ²：ｎ²に内分する点になるんですね。

　また、２円Ｃ₁、Ｃ₂の交点のｙ座標は、　ｙ＝±ｍｎ（ｂ−ａ）/（ｍ²＋ｎ²）となる。

　２円Ｃ₁、Ｃ₂の交点における接線の交点をＴ（ｔ，０）とすると、方べきの定理と直角三角形

の面積の計算から、ｔ＝（−ｎ²ａ＋ｍ²ｂ）/（ｍ²−ｎ²）であることが分かる。すなわち、Ｔ＝Ｃ₁

で、任意のｍ、ｎについて、２つの接線の交点はアポロニウスの円の中心となる。

　同様の議論を行えば、２点Ａ、Ｂを通る任意の円についても所要の性質があるように思われ

る。（証明は未完成）


　　以下、工事中！