ことを最近、茨城大学の仁平政一さんの書籍：
三角関数に関するある等式について （数研通信 Ｎｏ．６９ （数研出版））
で学ぶことができた。
例 ｓｉｎ１０°
この値は、らすかるさんの「三角関数表」にも載せられていない！それもそのはずで、この
値を求めるためには、θ＝１０°として、３次方程式 ８ｓｉｎ3θ−６ｓｉｎθ＋１＝０ を解かな
ければならない。３次方程式の解の公式があるとはいえ、これは少し大変そうだ。
ところが、１０°について、次のような美しい等式が成り立つことが知られている。
４ｓｉｎ１０°＋
ｔａｎ１０°＝１ ・・・ (*)このような等式による表現は、「チェビシェフの多項式」においても取り上げられている。
同様に、２０°については、 ４ｓｉｎ２０°＋ｔａｎ２０°＝
・・・ (**) が成り立つ。三角関数の諸公式を活用すれば、等式(*)、(**)を直接導くことは可能である。
(*)の証明： θ＝１０°とおくと、３θ＝３０°なので、２θ＝３０°−θ
よって、 ２ｓｉｎ２θ＝２ｓｉｎ（３０°−θ）＝ｃｏｓθ−
ｓｉｎθすなわち、 ４ｓｉｎθｃｏｓθ＝ｃｏｓθ−
ｓｉｎθ より、両辺をｃｏｓθで割って、４ｓｉｎθ＝１−
ｔａｎθ より、 ４ｓｉｎ１０°＋ｔａｎ１０°＝１ （証終）(**)の証明： θ＝２０°とおくと、３θ＝６０°なので、２θ＝６０°−θ
よって、 ２ｓｉｎ２θ＝２ｓｉｎ（６０°−θ）＝
ｃｏｓθ−ｓｉｎθすなわち、 ４ｓｉｎθｃｏｓθ＝
ｃｏｓθ−ｓｉｎθ より、両辺をｃｏｓθで割って、４ｓｉｎθ＝
−ｔａｎθ より、 ４ｓｉｎ２０°＋ｔａｎ２０°＝ （証終）次に、等式(*)、(**)を別な視点で証明することを考えよう。
Ｃ＝９０°の直角三角形ＡＢＣにおいて、∠ＡＢＣ＝θとおく。
今、１≦ｐ≦ｎ なる実数ｐ、ｎに対し、辺ＣＡ上に、∠ＤＢＣ＝（ｐ/ｎ）θとなる点Ｄをとる。
ＣＤ＝ｘ とおく。
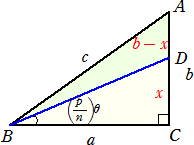
このとき、 ａ・ｓｉｎ（ｐ/ｎ）θ−ｂ・ｃｏｓ（ｐ/ｎ）θ＋ｃ・ｓｉｎ（１−ｐ/ｎ）θ＝０ が成り立つ。
（正弦定理を用いた証明）
△ＡＢＤにおいて、（ｂ−ｘ）/ｓｉｎ（１−ｐ/ｎ）θ＝ｃ/ｓｉｎ｛９０°＋（ｐ/ｎ）θ｝＝ｃ/ｃｏｓ（ｐ/ｎ）θ
なので、 ｂ・ｃｏｓ（ｐ/ｎ）θ−ｘ・ｃｏｓ（ｐ/ｎ）θ＝ｃ・ｓｉｎ（１−ｐ/ｎ）θ
ここで、 ｘ＝ａ・ｔａｎ（ｐ/ｎ）θ より、 ｘ・ｃｏｓ（ｐ/ｎ）θ＝ａ・ｓｉｎ（ｐ/ｎ）θ なので、
ｂ・ｃｏｓ（ｐ/ｎ）θ−ａ・ｓｉｎ（ｐ/ｎ）θ＝ｃ・ｓｉｎ（１−ｐ/ｎ）θ
すなわち、 ａ・ｓｉｎ（ｐ/ｎ）θ−ｂ・ｃｏｓ（ｐ/ｎ）θ＋ｃ・ｓｉｎ（１−ｐ/ｎ）θ＝０
が成り立つ。
（面積を用いた証明）
ＢＤ＝ａ/｛ｃｏｓ（ｐ/ｎ）θ｝ で、△ＡＢＤ＋△ＤＢＣ＝△ＡＢＣ より、
ｃａ/｛ｃｏｓ（ｐ/ｎ）θ｝・ｓｉｎ（１−ｐ/ｎ）θ＋ａ2/｛ｃｏｓ（ｐ/ｎ）θ｝・ｓｉｎ（ｐ/ｎ）θ＝ａｂ
よって、 ｃ・ｓｉｎ（１−ｐ/ｎ）θ＋ａ・ｓｉｎ（ｐ/ｎ）θ＝ｂ・ｃｏｓ（ｐ/ｎ）θ より、
ａ・ｓｉｎ（ｐ/ｎ）θ−ｂ・ｃｏｓ（ｐ/ｎ）θ＋ｃ・ｓｉｎ（１−ｐ/ｎ）θ＝０
が成り立つ。
等式(*)： ４ｓｉｎ１０°＋
ｔａｎ１０°＝１ 、(**)： ４ｓｉｎ２０°＋ｔａｎ２０°＝ は、上記で得られた等式を用いても示される。
ｐ＝１、ｎ＝３ として、 ａ・ｓｉｎ（１/３）θ−ｂ・ｃｏｓ（１/３）θ＋ｃ・ｓｉｎ（２/３）θ＝０ より、
ａ・ｓｉｎ（１/３）θ−ｂ・ｃｏｓ（１/３）θ＋２ｃ・ｓｉｎ（１/３）θｃｏｓ（１/３）θ＝０
両辺をｃｏｓ（１/３）θで割って、 ａ・ｔａｎ（１/３）θ−ｂ＋２ｃ・ｓｉｎ（１/３）θ＝０
(*)の証明： θ＝３０°とすると、ａ＝
、ｂ＝１、ｃ＝２としてよいので、ｔａｎ１０°−１＋４ｓｉｎ１０°＝０ すなわち、 ４ｓｉｎ１０°＋ｔａｎ１０°＝１(**)の証明： θ＝６０°とすると、ａ＝１、ｂ＝
、ｃ＝２としてよいので、ｔａｎ２０°−
＋４ｓｉｎ２０°＝０ すなわち、 ４ｓｉｎ２０°＋ｔａｎ２０°＝因みに、θ＝４５°とすると、ａ＝１、ｂ＝１、ｃ＝
としてよいので、ｔａｎ１５°−１＋２
ｓｉｎ１５°＝０ すなわち、 ２ｓｉｎ１５°＋ｔａｎ１５°＝１これより、次の等式が得られた。
２
ｓｉｎ１５°＋ｔａｎ１５°＝１ ・・・ (***)（別解） ｓｉｎ１５°＝（
−）/４ 、ｔａｎ１５°＝（−）/（＋）＝２−なので、 ２
ｓｉｎ１５°＋ｔａｎ１５°＝−１＋２−＝１ （終）因みに、ｓｉｎ１５°＝（
−）/４ 、ｔａｎ１５°＝２− という値は、加法定理を用いれば直ちに求められるが、次のようにしても求められる。
下図において、ＡＤ ： ＤＣ＝２ ：
なので、ＤＣ＝/（２＋）＝２−３
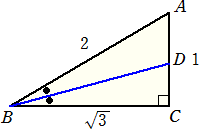よって、 ＢＤ＝３− なので、ｓｉｎ１５°＝（２
−３）/（３−）＝（−）/４ｔａｎ１５°＝（２
−３）/＝２−