Nを2以上の自然数とします。ある(都合のいい)三角形を合同なN個の図形に分割すること
を考えます。
N=2のときは二等辺三角形を用意して、頂点と底辺中点を結ぶ線を引けば合同に2分割
できます。(このように裏返しての合同でも構いません)
N=3のときは正三角形を用意して、中心と各辺中点を結ぶ線を引けば合同に3分割でき
ます。(このように分割後の図形は三角形以外でもかまいません)
このように続けていくとして、どのようなNなら分割可能でしょうか?
なお、30以下の範囲では、
N=2、3、4、5、6、8、9、10、12、13、16、17、18、20,24、25、26、27、29
は可能なことが私の手元ではわかっていますが、不可能証明できたものはありません。
らすかるさんからのコメントです。(平成27年4月1日付け)
書かれている数が分割可能なことはわかりましたので、「N=7が出来ないか」をしばらくあ
れこれ考えたのですが、まだ出来ません。もしかしたら出来ないのでしょうか。しかし、出来
ないとしても証明は難しそうですね。
(1) 2平方数の和で表せる数または3または6
(2) 平方数
(3) (1)と(2)の積
のときに分割可能なことはわかりましたが、他に出来るものはあるでしょうか。
(コメント) 面白い問題設定ですね!いくつか追認してみました。
N=4のとき、正三角形の各辺の中点を結ぶと4分割可能。
N=5のとき、次のような特殊な三角形を考えると5分割可能(この三角形は4分割も可能)
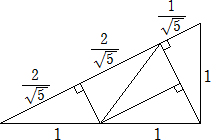
N=6のとき、N=3の場合から、さらに中心と各頂点を結んで分割すれば6分割可能。
