「不可能の証明」で岡 潔先生が思案されているのと同様に、「存在しない」ことを証明する
こともまた然りである。「存在する」を示すには、実際に存在するものを一つあげれば十分で
あるが、「存在しない」ことを示すには、ありとあらゆる場合を考えて本当に存在しないことを
相手に説得・納得させる必要があり、その労力たるや尋常ではない。
命題が真であることを示すには証明が必要であるが、命題が偽であることを示すには命題
が成り立たない反例の存在を示せば十分である。
「最大値Mを求めよ。」という問題は「Mを超えるものは存在しない」と同義で、「存在しない
ことの証明」の範疇に入るものと考えられる。
「存在する」を示すことは、「存在しない」ことを示すよりも格段に容易であり、「存在しない」
ことを示すことは、一般に困難である。その意味で「存在しないことの証明」は、悪魔の証明
とも言われる。
次の問題を皆さんはどのように考えるだろうか?
問題 連立不等式 x−2y≧3 、3x−y≧−2 、−4x+3y≧0 の解は存在するか?
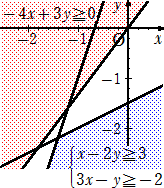
左図のように領域を求めてみれば、3式を同時に満たす(x,y)
は存在しないことが分かる。即ち、「解は存在しない」である。
上記の問題は、実は一瞬にして、解が存在しないことが分かる。
実際に、解(x,y)が存在するとすると、 x−2y≧3 、3x−y≧−2 、−4x+3y≧0
3式を辺々加えて、 0x+0y≧1 即ち、 0≧1 となり、これは矛盾である。
したがって、3式を同時に満たす(x,y)は存在しない。
(コメント) 上記のように、解が存在しないことを示すためには、図を描いたり、3式を加える
といった表現・技能が求められる。上記の問題はたまたま平易に示されたが、「存
在しないことの証明」には、その表現・技能を思案することが求められる。それが、
実は大変なのである。
