13+23+33+・・・・+n3=1×12+2×22+3×32+・・・・n×n2={n(n+1)/2}2
のよく知られた関係式は
一辺が1の正方形を1個、一辺が2の正方形を2個、・・・、一辺が n の正方形を n 個を使って、
一辺が n(n+1)/2 の正方形を敷き詰める可能性を示唆する。
さて、本当にこのことが実現されるのは、n がいくつのときだろうか?
n=12 すなわち、一辺が78の正方形について、敷き詰めが可能である。
実際に、その敷き詰め図は下図のようになる。
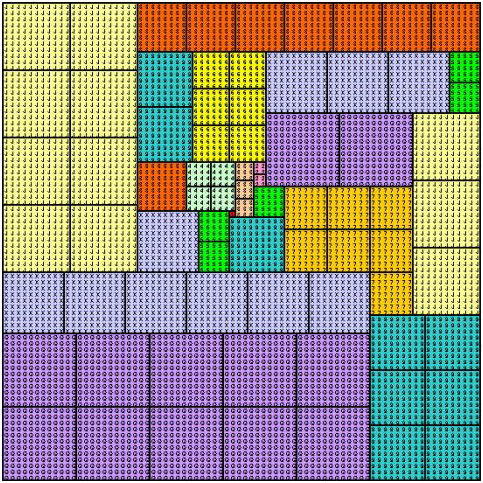
(コメント) 綺麗に敷き詰められていますね!感動しました。
通りすがりの匿名さんからのコメントです。(平成30年7月15日付け)
6月末に上記の話題が、Crさんのtwitterで紹介されました。
(このNicomachus's theoremのMrs. Perkins' Quiltでの可視化みたいなお話は、少なくとも
n=8、9、12、13 で出来るらしいとそのツイート関連でありました。)
ハンニバル・フォーチュンさんからのコメントです。(平成30年7月20日付け)
GAIさんによる以下の提案に興味を引かれました。
13+23+33+・・・・+n3=1×12+2×22+3×32+・・・・n×n2={n(n+1)/2}2
のよく知られた関係式は
一辺が1の正方形を1個、一辺が2の正方形を2個、・・・、一辺が n の正方形を n 個を使って、
一辺が n(n+1)/2 の正方形を敷き詰める可能性を示唆する。
この敷き詰めは簡単にはいかないようでして、通りすがりの匿名さんからのコメントからも
その困難さを伺いしれます。
さて、以下のように工夫しなおした関係式ならば、正方形による敷き詰めはごくごく簡単に
なります。
4×(13+23+・・・+n3)=4×1×12+4×2×22+・・・4×n×n2=n2(n+1)2
の関係式を導いておいて、
一辺が1の正方形を4×1個、一辺が2の正方形を4×2個、・・・、一辺が n の正方形を
4×n個を使って、一辺が n(n+1)の正方形を敷き詰める可能性を示唆する。
実際にやってみると、すぐに敷き詰められます。
一辺が1の正方形を4個固めて一辺が2の正方形にして紙の中央に書きます。そのまわり
に一辺が2の正方形を8個ぐるりと囲むように配置して書きます。全体で正方形になります。
そのまわりに一辺が3の正方形を12個ぐるりと囲むように配置して書きます。全体で正方形
になります。……以下同様にnまで行います。
以上については、クヌースの「基本算法」に若干のコメントと挿し絵だけが書かれていたよ
うな記憶があります。
(コメント) なるほど!簡明ですね。ということは、nは任意で可能ということですね。何となく
解の公式を証明するのに、方程式を4倍する感覚に似ていますね。ハンニバル・
フォーチュンさんに感謝します。

