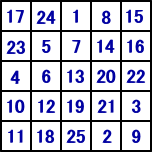
を考える。
因みに、5×5魔方陣は全部で、2億7530万5224種類ある。(→ 参考:「魔方陣の話題」)
上記の数字を順番と考え、πでの数字へ変換してみると、
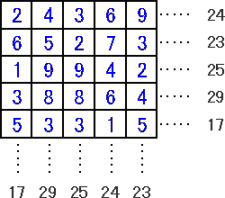
こんな偶然ってあり?
(コメント) 多分、偶然...!? 3×3魔方陣では同様の性質は見いだせませんでした。

・円周率で魔方陣もどき GAI 氏
円周率 π を小数点以下100桁まで表示すると、次のようである。
| π | = | 3. | 1415 | 9265 | 3589 | 7932 | 3846 | 2643 | 3832 | 7950 | 2884 | 1971 | 6939 |
| 9375 | 1058 | 2097 | 4944 | 5923 | 0781 | 6406 | 2862 | 0899 | 8628 | 0348 | |||
| 2534 | 2117 | 0679 | ・・・・・ | ・・・・・ | ・・・・・ | ・・・・・ | ・・・・・ | ・・・・・ | ・・・・・ | ・・・・・ |
これらの出現する数字に最初から25番目まで順に番号をつけて、
| 順番 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 数字 | 3 | 1 | 4 | 1 | 5 | 9 | 2 | 6 | 5 | 3 | 5 | 8 | 9 | 7 | 9 | 3 | 2 | 3 | 8 | 4 | 6 | 2 | 6 | 4 | 3 |
としておく。ここに、5×5魔方陣(縦・横・斜めの各和は65)の一つ

を考える。
因みに、5×5魔方陣は全部で、2億7530万5224種類ある。(→ 参考:「魔方陣の話題」)
上記の数字を順番と考え、πでの数字へ変換してみると、

こんな偶然ってあり?
(コメント) 多分、偶然...!? 3×3魔方陣では同様の性質は見いだせませんでした。
