・１８度の正弦 よおすけ 氏
以下に挙げるのは、ｓｉｎ１８°の値を求める解法である。
まず、ｚについての方程式をつくるため、 ｚ＝ｃｏｓ１８°＋ｉ・ｓｉｎ１８°と置く。ただし、ｉ
は
虚数単位とする。
両辺を５乗して、 ｚ5＝（ｃｏｓ１８°＋ｉ・ｓｉｎ１８°）5＝ｃｏｓ９０°＋ｉ・ｓｉｎ９０°＝ ｉ
このとき、 ｚ5＝ ｉ＝ ｉ5 と考えて、 （ｚ−ｉ）（ｚ4＋ｉ・ｚ3−ｚ2−ｉ・ｚ＋１）＝０
ここで、明らかに、 ｚ−ｉ≠０ なので、 ｚ4＋ｉ・ｚ3−ｚ2−ｉ・ｚ＋１＝０
また、ｚ≠0 なので、両辺を ｚ2 で割ると、
ｚ2＋ｉ・ｚ−１−ｉ・（１/ｚ）＋１/ｚ2＝０
すなわち、 （ｚ−１/ｚ）2＋ｉ・（ｚ−１/ｚ）＋１＝０
これより、 （ｚ−１/ｚ＋ｉ/２）2＝−５/４ なので、 ｚ−１/ｚ＋ｉ/２＝±ｉ
/２
よって、 ｚ−１/ｚ＝（−１±）ｉ/２ となる。
ここで、 １/ｚ＝ｚ-1＝ｃｏｓ１８°−ｉ・ｓｉｎ１８°なので、 ｚ−１/ｚ＝２ｉ・ｓｉｎ１８°
よって、 ｓｉｎ１８°＝（−１±）/４ となる。
ここで、１８°は鋭角なので、 ｓｉｎ１８°＞０ より、 ｓｉｎ１８°＝（−１＋）/４
（ｓｉｎ１８°の解法ではネットではほとんどみかけないものを書きました。）
（コメント） よおすけ様、ありがとうございます。複素数を用いて実数値を求める発想は数
学の世界では大切なアイデアですよね！
実数の世界だけで、ｓｉｎ１８°の値を求めたい場合は、 θ＝１８°として、
ｓｉｎ３θ＝ｃｏｓ（９０°−２θ）＝ｓｉｎ２θ から、
４ｓｉｎ3θ−２ｓｉｎ2θ−３ｓｉｎθ＋１＝０
すなわち、 （ｓｉｎθ−１）（４ｓｉｎ2θ＋２ｓｉｎθ−１）＝０
４ｓｉｎ2θ＋２ｓｉｎθ−１＝０ から、 ｓｉｎθ＝（−１±）/４
ｓｉｎθ＞０ なので、 ｓｉｎθ＝（−１＋）/４
この求め方が、私としては一番のお気に入りです。
（追記） 平成２年１０月３日付け
当ＨＰがいつもお世話になっているＨＮ「らすかる」」さんは、次のように、図形的に求める
方法がお気に入りとのこと。
 |
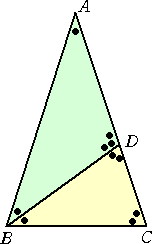頂角Ａ＝３６°、底角Ｂ、Ｃ＝７２°の二等辺三角形で
∠Ｂの二等分線とＡＣの交点をＤとし、
ＡＢ＝ＡＣ＝１、ＡＤ＝ＢＤ＝ＢＣ＝２ｘ（＞０）とすると、
ＡＣ ： ＢＣ ＝ ＢＣ ： ＣＤ から、 １ ： ２ｘ ＝ ２ｘ ： １−２ｘ
より、 ４ｘ2＋２ｘ−１＝０
これを解いて、 ｓｉｎ１８°＝ｘ＝（−１＋）/４ |
正五角形の対角線の長さを求めても得られる（→参考：「正５角形の作図と折り紙」）が、
上図の二等辺三角形が何か綺麗な三角形なのと、図形的によく見える解法ということで、
ＨＮ「ｔｅｔｓｕｙａ」さんも、上記の図形による解法を個人的には気に入っているとのことであ
る。
（追記） 平成２３年１２月７日付け
２年前、ｓｉｎ１８°の値を複素数を使って求めた解法を、ｃｏｓ７２°の解法を真似て、上記
のように紹介しました。その後、他の解答も・・・。いろいろあるんだ・・・って。
でも、何れも２次方程式を用いていることに変わりはありませんでした。二等辺三角形を
用いて、辺の比を使うとしても、結局は２次方程式ですし・・・。
２次方程式を使わず、ｓｉｎ１８°の値を求める方法はないか。これが自分が気になってい
ることです。
ＦＮさんからのコメントです。（平成２３年１２月８日付け）
ｓｉｎ１８°=(−１)/４ と「√」がついてますから、２次方程式を使わずに、ｓｉｎ１８°の値
を求めることは不可能です。見掛け上、２次方程式を解いてないように見える方法は、ある
いは可能かもしれませんが、実際には、２次方程式を解いてるはずです。
（追伸） 「これは当たり前だから、見掛け上２次方程式を使わない方法はないか」ということ
でしょうか。例えば、縦横が１と２の長方形の対角線の長さとかを使って、ｓｉｎ１８°が
表せないかというようなことでしょうか？
（追記） 平成２３年１２月８日付け
２次方程式なしでは、ｓｉｎ１８°の値を求めるのは事実上不可能ですか。「正五角形の作
図と折り紙」のページにある、正五角形をコンパスで作図を見ていたら、みかけ上は対角線
の長さを、辺の比を使わずに求められるかな・・と。その後、ｓｉｎ１８°の値を求める・・・だっ
たのですが、やはり、これも不可能だなって。
