と 
が異なることは自明だろう。でも、「
と ４ は等しい？」と問われれば、戸惑う人が多いだろう。答は、「等しい」なのだが、ある程度の計算力が必
要だ。（→ 参考：「２重根号」）
一般の方が、同じかどうかを判断する場合、直ぐ思いつくのは、比較する数のおおよその
値を電卓等で計算することだろう。
たとえば、
の値を電卓（または Ｅｘｃｅｌ）で計算してみると、確かに、４．００００００００００・・・・ となって、「４」だろうことは分かる。
ただ、この手法では、小数点以下数桁しか吟味していないので、きっちり等しいと言えな
い弱さを併せ持つ。
たとえば、
と 
のそれぞれの値を家庭に普及している８桁の電卓で計算してみると、
前者は、 １６２９．２５９７ で、後者は、 １６２９．２５９８
Ｅｘｃｅｌ でも計算してみると、
前者は、１６２９．２５９８８８６３３１４・・・ 、後者は、１６２９．２５９８８８６３０１９・・・
となり、小数点以下第８位までが一致している。
両者は明白に異なるので、２数は等しくないと断言できるが、小数点以下で同じ数字が
並ぶ場合は、２数の相等は微妙で、注意が必要だ。
したがって、電卓で計算しても、２数が一致する、しないを判断することは難しい。
このような話題は昔からあるようで、きっちりクッキリ計算しているところがエライ！
次の問題は、インドの数学者 バスカラの問題として有名である。
＝
これは、電卓に頼らず、直接の代数計算で示される。
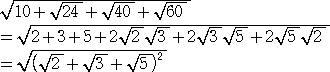
から、
になることは明かだろう。（コメント） 複雑そうに見える式でも、工夫すると簡単になる場合があるんですね！
