平行でない2本の直線が必ず1点で交わることはユークリッド幾何の教える所である。
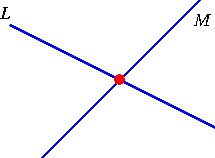
いま上図に次のような性質をもつ1個の円と1本の直線を組にして順次書き加える。
(イ) 円の中心は、常に直線 L と直線 M との交点である。
(ロ) 書き加える直線は直線 L と直線 M の交点を常に通る。
(ハ) 書き加えられた円は何れも重ならない。
(ニ) 書き加えられたどの直線も、それまでに書き加えられた直線および直線 L 、M と
は重ならない。
n 個の円と n 本の直線を書き加えたときの交点の数を、an とおくことにする。
たとえば、n=1 のとき、
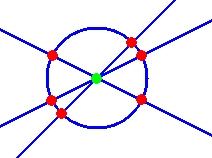
明らかに、 a1=7 である。
次に、n=2 のとき、
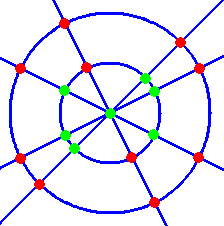
明らかに、 a2=17 である。
一般に、an を n の式で表すことが目標である。
さて、この交点を数え上げる方法として、次の2つが考えられる。
(方法1) 1個の円と1本の直線を書き加えた場合に増加する交点数に注目する方法
(方法2) 1個の円と1本の直線を書き加えて得られる図の交点数を一括で求める方法
(1個の円と1本の直線の交点数は常に2であるという性質が活躍する!)
(方法1)は漸化式を考えるときの基本的思考であるが、この場合は仇となる。(方法2)
で考えると混乱なく容易に交点数を直接的に求めることが出来る。ここら辺がこの問題の
急所であり、作問者が仕掛けたトラップ(罠)なのだろう。
いま、直線 L と直線 M が交わっている図に、n−1 個の円と n−1 本の直線が書き
加えられているものとする。ただし、n≧1 とする。
その図に、さらに、1 個の円と 1 本の直線を書き加える。すると、その図には、n 個の
円と n+2 本の直線があるので、交点の総数は、直線 L と直線 M との交点も含めて、
an = 2×(n+2)×n+1 = 2n2+4n+1
となる。
(方法1)による解法が如何に大変かは、次の計算を見れば了解されるだろう。
いま、直線 L と直線 M が交わっている図に、n 個の円と n 本の直線が書き加えられて
いるものとする。ただし、n≧1 とする。このときの交点数が、an である。
その図に、さらに、1 個の円と 1 本の直線を書き加えたときの交点数が、an+1 である。
交点の増加数を求めよう。
書き加えた円は、 n+3 本の直線と新規に交わるので、その交点数は、 2(n+3)
書き加えた直線は、もとの n 個の円と新規に交わるので、その交点数は、 2n
したがって、 an+1 = an + 2(n+3) +2n = an + 4n+6
a1=7 なので、この漸化式を解くと、(→参考:「漸化式の全て」)
an = 2n2+4n+1
となる。
