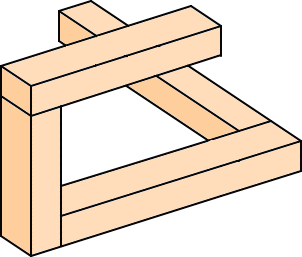
・　不可能物体を作る　　 　　　　　　　　　　　　　Ｓ．Ｈ氏

　実際には作製困難だが、絵として人を魅了する物体がある。人はそれを不可能物体と称
する。エッシャーや安野光雅の作品にも見受けられる。

　ここでは、不可能と言われる物体を人間の目を誤魔化すことによって作製してみた。

　左下の絵は何ら不自然なところはないが、右下のような奇妙な絵にすると、何か変だ！

→

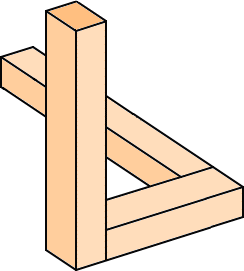
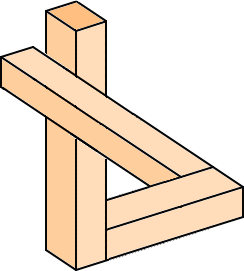
　上図では、線を書き加えたり消したりすることによって、不可能物体を作っている。このよ
うに、絵として不可能物体を作ることは比較的容易である。

　それでは、不可能物体を作ることは本当に不可能なのだろうか？

　もちろん、それは「ｙｅｓ！」であるが、あえてそれに挑戦してみた。

　　　　　　　　　　　

　何となく不可能物体に見えないだろうか？（ちょっと作り方が稚拙かな？）

　また、左下の絵をもとに、右下のような奇妙な絵を描くことが出来る。絵は数学と同じで、
発想が自由自在である。そこが、また魅力的なところでもある。

→

（参考文献：杉原厚吉　著　　立体イリュージョンの数理　（共立出版））


（追記）　平成２４年４月２８日付け

　１９８１年にオーストリアで「不可能物体」を描いた郵便切手が発行された。とても魅惑的な
立体だったので模写してみた。

　　　　　　　　　　　　　　

（参考文献：アルフレッド・Ｓ．ポザマンティエ　イングマール・レーマン　著
　　　　　　　　坂井　公　訳　　偏愛的数学　　魅惑の図形　（岩波書店））


（追記）　令和３年１０月３日付け

　作れそうにないと感じるのに、何故か立体感を持つので、人間は騙される。そのような騙
し絵として、ペンローズの三角形がつとに有名である。

　　　 　　　　　　　　　　

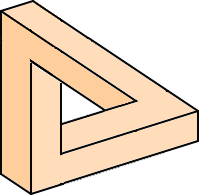
　だまし絵研究の創始者としては、ペンローズ父子の名前があげられる。

　最近、杉原厚吉　著　「だまし絵のトリック」（化学同人）　を読んでいて、「無限階段」のこと
に興味を持ち、実際に絵を描いてみた。拙い絵で、人間の目を騙すには、まだまだ修行不足
ですね！

　本物は、Ｒ．Ｐｅｎｒｏｓｅ（１９５８）の作品のようだ。



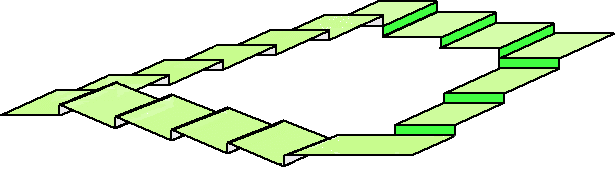
　上図を少し手直ししてみた。



　少しは無限階段のように見えるようになったかな？


（追記）　令和３年１０月２６日付け

　不可能物体を作るためには、扱う図形の常識から脱却する必要がある。

　杉原氏によれば、立体化のトリックが少なくとも３つあるとのことである。

・不連続のトリック・・・繋がっているように見えるところにギャップを設ける。（→　例）

・曲面のトリック・・・曲面を平面のように見せる。

・非直角のトリック・・・直角以外の角度を用いて、直角に見せる。（→　脳は直角が好き！）


　一つの平面図形から、投影してその図形になる立体図形は、数学的には無限の可能性
がある。この性質を利用して、不可能物体があたかも実在するかのように作ることが可能
になるのである。すなわち、奥行きがいろいろな可能性を秘めているということである。

例　ここに立方体がある。

　　　　

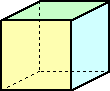
　次の立体図形は、見る角度を変えると、立方体に見える瞬間がある。

　　　

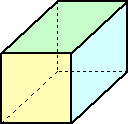
　つまり、今見ている立体図形が、実は、立方体もどきで、いろいろな可能性があるというこ
とを意味する。


　読者の方のために、練習問題を残しておこう。

練習問題　　ある立体図形を、上、前、横から見たら、次のような図形になるという。
　　　　　　　元の図形は、どんな図形であろうか？

	上から見た図		前から見た図		横から見た図
	三角形		正方形		円

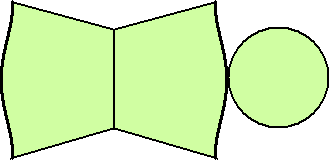
（解）　答の一例として、

　　　


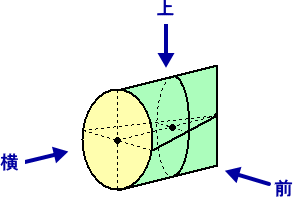
　何となく、歯磨き粉のチューブに似ているかな．．．？


　カルピスさんからのコメントです。（令和３年１０月２９日付け）

　コーヒー飲んだら眠れなくなってしまった。。

　上から三角、横から真四角、前から円

の答えを見て、「トイレットペーパーの芯」の片側を潰した形ですね。
（芯の長さを直径の長さで切って）

　では、この立体の展開図は？　と聞かれたら、ただの長方形？　と答えて良いのだろうか？

　あっ！トイレットペーパーの芯の輪を潰すと、輪の直径より長くなってしまう・・・（ＴＴ）


　ＧＡＩ さんからのコメントです。（令和３年１０月２９日付け）

　素晴らしい観察力。紙コップですね。（飲み口の半径がRの時、底は2R/πの半径で）

　カルピスさんからのコメントです。（令和３年１０月２９日付け）

　ＧＡＩさん、有難うございます。そうですね。紙コップのように、徐々に輪が小さくなっていく物
でないと、成り立たなくなってしまいますね。

　上図の歯磨き粉のチューブも、底の方に移動するに連れて、徐々に輪が小さくなっている
のかな。。　どーでもいい雑談でした。。。


（コメント）　展開図は、長方形にはならないと思います。多分、次のような形かな？

　　　　　　　　


　Dengan kesaktian Indukmu さんからのコメントです。（令和３年１０月２９日付け）

　ふと思い出しました。それは、ダグラス・R・ホフスタッター著の「ゲーデル、エッシャー、バッ
ハ　あるいは不思議の環」の第１版（出版社 白揚社 刊行年 1985年）の表紙絵です。

　現在刊行されている同書の表紙絵はガラッと変わってしまっていますけれども、私が思い
出したのは、変わる前の第１版のそれです。

　その表紙絵の中央には、木彫りの立体オブジェが配置されています。 そのオブジェに三
方向から光をあてて影をみると、それぞれ「Ｇ」「Ｅ」「Ｂ」となっているのでした。

　不可能物体とはいえないのかもしれませんが、なんとも不思議な印象を与えるものでした。

※「Ｇ」「Ｅ」「Ｂ」は、ゲーデル、エッシャー、バッハの頭文字です。

※ネット上では古書の取り扱いをしているサイトで、同書の表紙絵をみることができるかもし
　れません。たとえば、参考などで．．．。

　　　　　　



　　以下、工事中！