2025 = 1^3 + 2^3 + 3^3 + 4^3 + 5^3 + 6^3 + 7^3 + 8^3 + 9^3
・2025は45の平方数です。
・45は、1から9までの自然数の和 (1 + 2 + 3 + ... + 9) に等しいです。
・一般に、1からnまでの自然数の立方数の和は、[(n(n+1))/2]^2、つまり、n番目の三角数
の平方に等しいです。
※下図は、n=4 のときの直感的な理解を助けるものです。

n=9 の図を描きたかったのですが途中でめげました。とほほ
らすかるさんからのコメントです。(令和6年12月12日付け)
今ここを見ている人は多分、最初で最後の平方数年でしょうね。
(コメント) 2025=45×45 で、次の平方数年は、46×46=2116 で、91年後!
そこまで、長生きできそうにない...。
ks さんからのコメントです。(令和6年12月19日付け)
2025=45^2
2025=a^2+b^2+c^2 を満たす自然数a,b,cを求めるといくつあるでしょうか?
らすかるさんからのコメントです。(令和6年12月19日付け)
a≦b≦c として、11組です。
(4,28,35)、(5,8,44)、(5,20,40)、(6,15,42)、(6,30,33)、(8,19,40)、(13,16,40)、(15,30,30)、(16,20,37)
(20,20,35)、(20,28,29)
a≦b≦c の条件を外すと、9×6+2×3=60(通り)となります。
(追記) 令和7年2月2日付け
「2025」には、いろいろな意味づけが可能ですね!
Dengan kesaktian Indukmu さんの
・2025 = 1^3 + 2^3 + 3^3 + 4^3 + 5^3 + 6^3 + 7^3 + 8^3 + 9^3
には目を見張りました。最近、灘中学入試(2025)の問題を検討していて、次の話題にも興
味を引かれました。
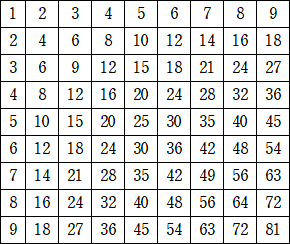
上記の表は、掛け算の九九で、1×1から9×9までをまとめたものである。
この81個の数を全部足すと、2025 となる。
実際に、 1×1+・・・+9×9
=1×(1+2+・・・+9)+・・・+9×(1+2+・・・+9)=(1+2+・・・+9)2=2025
九九の計算結果の総和が「2025」になるなんて気にも留めていなかったので、新鮮でした。
また、下図のように、9×9のマス目があって、その中に含まれる長方形の総数も2025個
であることにも驚かされました。

実際に、10本の縦の罫線から2本を選び、10本の横の罫線から2本を選ぶと、1個の長方
形が定まるので、求める長方形の総数は、 10C2・10C2=45×45=2025(個) である。
カルピスさんからのコメントです。(令和7年3月14日付け)
コーヒーブレイク in スタバ です。小学校の頃、九九が全部言えなくて、放課後、残され
た。私にとって、九九は苦苦だった。
九九の答えの表には81個の数字が書かれているが、この81個の数字を全部足すと2025
になると、今年(2025年)に初めて知った。ちょっと感動・・・・・。
ここで、問題を思いついた。
問題 11、13、17、19、22、□
□に入る数は?
(コメント) 九九の表に現れない数字を小さい順に並べたものと考えると、答えは、「23」かな?。
カルピスさんからのコメントです。(令和7年3月14日付け)
正解です!
GAI さんからのコメントです。(令和7年3月14日付け)
1、2、3、5、7、11、13、17、19、22、23、25、26、29、・・・ と続いていく数列の次の10個の数
は何でしょう?
(コメント) 「A246281」によれば、31、33、34、37、38、41、43、46、47、51 ですか?
GAI さんからのコメントです。(令和7年3月15日付け)
正解です!
必ず素数は入っているが、それ以外にも合成数が時々入り込めるところが面白い。ベルト
ランの仮説がここから発生しているらしく、よくもこんな性質に着目できるものだと感心します。
また、これを証明したチェビシェフの能力にも脱帽です。
カルピスさんからのコメントです。(令和7年3月15日付け)
小学2年生の、おじゃま虫:「九九の研究」です。
九九の表には81個の答えがあるが、重複しているものを消すと45個になる。
1〜81の中で、九九の答に無いものは45個 ・・・ これは偶然の一致???
スピリチュアルの江原啓之さん曰く:この世には偶然はなく全て必然に起こる。
私の頭がボケてるだけ???
(コメント) なるほど、そういう見方も出来るんですね!
でも、重複しているものを消すと36個?
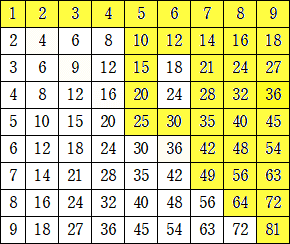
カルピスさんからのコメントです。(令和7年3月16日付け)
九九の表を斜めに、約、真っ二つにしただけでした。正確には36個でしたね(^^;
カルピスさんからのコメントです。(令和7年3月17日付け)
今更ながら・・・・・私の表現の仕方が悪かったです。
【九九の重複】の意味は、下記のような、答えの重複ではなく
1x6=6
2x3=6
「式の重複」(3x4=12 や 4x3=12 など)を意図としていました。
これらを1通りと考えると、45個になり、九九の答えに無い数字の個数45個と同じになる。
以下、工事中!
