���w�������ɒ���I�i���̂Q�j�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�ߘa�U�N�x�咆�w�̓����́A�P���P�R���E�P�S���̗����s��ꂽ�B�P���ځE�Q���ڂƂQ����
�s���A�Z���ɋ������w�����W�߂����Ƃ����w�Z�̎v�f���\�����ݎ���������ƂȂ�
�Ă���B�������ʔ��������A���w���ɂȂ�������ʼn����Ă݂��B
�i�P���ځj
��Q���@���Y�N�͂P�{�̒l�i�����~�̃y�����T�{�����\��ł������A���������P�Q�O�~����
�@�܂���ł����B����ɁA�P�{�̒l�i���\�肵�Ă������̂��P�O�O�~�����y�����V�{�ƂU�O
�@�~�̏����S�����P�������Ƃ���A���傤�Ǐ��������g����܂����B���ɓ��Ă͂܂鐔��
�@�����B
�i���j�@��ӂ��A�@���~�T�|�P�Q�O���i���|�P�O�O�j�~�V�{�U�O�@�Ȃ̂ŁA
�@���~�Q���V�O�O�|�U�O�|�P�Q�O���T�Q�O�@���A�@�����Q�U�O�@�@�i�I�j
��R���@����w�Z�̐��k�ɁAA�AB�AC �̂R�̒��ɍs�������Ƃ����邩�ǂ����̒���������
�@�Ƃ���AA�AB�AC �ɍs�������Ƃ����鐶�k�̊����͂��ꂼ��S�̂� �Q/�V�A�T/�P�S�A�P/�X ��
�@�����BA��B�̗����ɍs�������Ƃ����鐶�k�̊����͑S�̂̂P/�S�ł����B�܂��AC�ɍs����
�@���Ƃ����鐶�k�͑S���AA�ɂ�B�ɂ��s�������Ƃ�����܂���ł����BA�AB�AC �̂ǂ̒��ɂ�
�@�s�������Ƃ��Ȃ����k�͂X�X�X�l�ȉ��ł����BA�AB�AC �̂ǂ̒��ɂ��s�������Ƃ��Ȃ����k
�@�̐l���Ƃ��čl��������̂̂����ł��������̂́��l�ł��B���ɓ��Ă͂܂鐔�͉����B
�i���j�@�����ő�ɂȂ�ꍇ�A
�@A�̒��݂̂ɍs�������Ƃ����鐶�k�̊����́A�P/�Q�W
�@B�̒��݂̂ɍs�������Ƃ����鐶�k�̊����́A�R/�Q�W
�@A�AB�̒��̗����ɍs�������Ƃ����鐶�k�̊����́A�V/�Q�W
�@C�̒��݂̂ɍs�������Ƃ����鐶�k�̊����́A�P/�X
���AA�AB�AC �̂ǂ̒��ɂ��s�������Ƃ��Ȃ����k�̊����́A
�@�P�|�i�P�P/�Q�W�{�P/�X�j���P�Q�T/�Q�T�Q
�@���ꂪ�X�X�X�l�ȉ��ƂȂ�ő�l�́A�@�i�P�Q�T/�Q�T�Q�j�~�i�V�~�Q�T�Q�j���W�V�T�i�l�j�@�@�i�I�j
��S���@A����B�������ԓ�������܂��B���̓���������̃o�X��A������B���Ɍ���������
�@�Ɉ��̑����ŁA���̊Ԋu�ő����Ă��܂��B
�@���Y�N�����������AA������B���Ɍ����������Ɉ��̑����Ŏ��]�Ԃő���ƁA�o�X�ɂQ�O
�����Ƃɒǂ��z����܂����B���Y�N�����̂܂܂̑����ő�������݂̂ɕς���ƁA�o
�X�ɂP�O�����Ƃɏo�����܂����B���̌�A���Y�N�������������Ukm�グ���Ƃ���A�o�X�ɂX��
���Ƃɏo�����܂����B�o�X�Ƃ��̎��̃o�X�̊Ԋu�����߂�B�������A�p�X�Ǝ��]�Ԃ̒�����
�l���Ȃ����̂Ƃ��܂��B
�i���j�@�o�X�̑��������i���j�A���]�Ԃ̑��������i���j�Ƃ��A�o�X�̊Ԋu���k�i���j�Ƃ����ƁA
�����Ukm�������P�O�Om �Ȃ̂ŁA��ӂ��A
�@�i���|���j�~�Q�O���k�@�A�i���{���j�~�P�O���k�@�A�i���{���{�P�O�O�j�~�X���k
��P���Ƒ�Q�����A�@�����R���@�Ȃ̂ŁA�@�S�O�����X�i�S���{�P�O�O�j�@���A�@�����Q�Q�T
����āA�@�k���S�O�����X�O�O�O�i���j�@����A�o�X�̊Ԋu�́A�@�X�����@�ł���B�@�@�i�I�j
�i�ʉ��j�@�o�X�̑��������i���j�A���]�Ԃ̑��������i���j�Ƃ��A�o�X�̊Ԋu���k�i���j�Ƃ����ƁA
�����Ukm�������P�O�Om �Ȃ̂ŁA��ӂ��A
�@���|�� �F ���{�� �F ���{���{�P�O�O���k/�Q�O �F �k/�P�O �F �k/�X���X �F �P�W �F �Q�O
���̂Ƃ��A���萔�� �� �Ƃ��āA�@�����i�Q�V/�Q�j���@�A�����i�X/�Q�j���@�Ȃ̂ŁA
�@�i�Q�V/�Q�j���{�i�X/�Q�j���{�P�O�O���Q�O���@�������āA�@�����T�O
�@����āA�o�X�̊Ԋu�́A�@�P�W���~�P�O���X�O�O�O�i���j�@���Ȃ킿�A�@�X���� �ł���B�@�@�i�I�j
�i�R�����g�j�@�A���������𗧂Ă�ΊȒP�ł��邪�A�Z���I�ɂ͂ǂ������̂��낤�H
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�R���S���t���j
�@��S��Ȃ�ł����A����A���Ƃ��ďo���������悤�Ɏv���܂��B
�i���邢�́A�Z���̃Z���X������q��I�肷���邽�߂ɂ킴�ƁH�j
�@�o�X�Ƌt������ 90 ���ԑ��邱�Ƃ��l���܂��B���X�̑������Ƒ��Y����� 90 ����� 9 ���
�̃o�X�̈ʒu�܂Ői�݁A�ύX��̑��x�̏ꍇ�� 90 ����� 10 ��ڂ̃o�X�̈ʒu�܂Ői��
�܂��B
�@�܂�A���Y���� 90 ���Ői�����̍� 6km/h * (90/60)h = 9km ���A9 ��ڂ̃o�X��
10 ��ڂ̃o�X�̊Ԋu�ł��̂ŁA������ 9km �ł��B
�c�c�ŏ��̒ǂ��������b�͂Ȃ�����ł��傤�H
�i�R�����g�j�@�Ȃ�قǁIDD++ ����̂悤�ɍl����A�u�o�X�ɂQ�O�����Ƃɒǂ��z����܂����v
�@�@�@�@�Ƃ��������͎g��Ȃ��čςނ�ł��ˁB�������A�A������������K�v�Ȃ��ƁD�D�D�B
�@�P�O���ōs�����Ƃ�����A�������P�O�O�����������ƂX���ōs����ƍl��������Ƃ���
���ƂŁA
�@�o�X�̊Ԋu���k�i���j�Ƃ���ƁA��ӂ��A�@�k/�X�|�k/�P�O���P�O�O ����A�k���X�O�O�O
���Ȃ킿�A�o�X�̊Ԋu�́A�X���� �ł���B
�i�R�����g�j�@���w�̃Z���X������邢�����ł��ˁI
�@�@�V����������^���Ă���������DD++ ����Ɋ��ӂ��܂��B
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�R���T���t���j
�@��L�R�����g�̉��āA�͒ʂ��Ă��ł��傤���H�Е��� 9 ���ŕЕ��� 10 �����ƁA�o
�X�̐i�������ς���Ă����ł����c�c�B
�i�R�����g�j�@�o�X���P�O���œ��B���������𑬂��𑝂������]�Ԃ��X���œ��B�����ƍl������
�@�@�@�@�@�ł����D�D�D�B���x�́A���Α��x�@�o�X�̑��x�{���]�Ԃ̑��x�@�Ōv�Z���Ă��܂��B
�@DD++ ����̃R�����g�ł��B�i�ߘa�U�N�R���U���t���j
�@�P���l���āA����Ɨ������܂����B
�@�o�X�i�Ǝ��]�ԁj���P�O���œ��B���������i�̍��v�j���i�o�X�Ɓj�����𑝂������]�Ԃ��X����
���B�����i�̂ŁA���ꂼ��̑��Α��x��\�����Ƃŕ������𗧂Ă��j
�ŁA���������Ă܂����H
�i�R�����g�j�@�����Ă���Ǝv���܂��B����ɂ��Ă��A�u�o�X�ɂQ�O�����Ƃɒǂ��z����܂����v��
�@�@�@�@�����������g�킸�ɉ����Ă��܂��͉̂��Ȃ̂ł��傤�ˁH
�@�o�X�̑��������i���j�A���]�Ԃ̑��������i���j�Ƃ��A���A�� ��ʌɋ��߂�ɂ́A�u�o�X��
�Q�O�����Ƃɒǂ��z����܂����v�̏������K�v�ł����A�o�X�̊Ԋu �k�i���j�����߂邾������
����A���Α��x ���{�� ��������Ώ\���ŁA���̂��Ƃ́A������������咆�w�̏o��҂̕���
�C�����Ȃ������̂�������Ȃ��ł��ˁI�i�����A�z������ȁH�j
��T���@���̖₢�ɓ�����B
�i�P�j�@�S���̃J�[�h�O�A�Q�A�Q�A�S ������Ƃ��A���̂S���̃J�[�h����ׂĂł���S���̐��̂���
�@�P�P�Ŋ�������̂͑S���ʼn�����܂����B�������A�u�O�Q�Q�S�v�͂S���̐��ł͂���܂�
�@��B
�i�Q�j�@�T���̃J�[�h�O�A�Q�A�Q�A�S�A�U ������Ƃ��A���̂����̂S���̃J�[�h����ׂĂł���S����
�@���̂����P�P�Ŋ�������̂͑S���ʼn�����܂����B�������A�U�̃J�[�h���㉺�t�ɂ���
�@�X�Ƃ��ėp���邱�Ƃ͂ł��܂���B
�i���j�i�P�j�@�S���̃J�[�h����ׂĂł���S���̐��͑S���ŁA�@�S�I/�Q�I�|�R�I/�Q�I���X�i�ʂ�j
�@���ۂɁA
�@�Q�O�Q�S�@�A�Q�O�S�Q�@�A�Q�Q�O�S�@�A�Q�Q�S�O�@�A�Q�S�O�Q�@�A�Q�S�Q�O�@�A�S�O�Q�Q�@�A�S�Q�O�Q�@�A�S�Q�Q�O
���̂����A�P�P�Ŋ�������̂́A�@�Q�O�Q�S�@�A�Q�S�Q�O�@�A�S�Q�O�Q�@�̂R�ʂ�
���i�P�j������������A�l�ׂ��ɒ��ׂ邾���ʼn����邪�A�i�Q�j���l����ƁA���������H�v���K�v
�@�ł���B
�i�ʉ��j�@�u�P�P�̔{���̔����v����A���̌������m���Ă���B
�@�S���̐� �`�a�b�c ���P�P�̔{���ƂȂ邽�߂ɂ́A�@�`�|�a�{�b�|�c ���P�P�̔{���ł�
�邱�Ƃ��K�v�\���ł���B
�@�{��̏ꍇ�A�`�A�a�A�b�A�c �́A�O�A�Q�A�Q�A�S �̉��ꂩ�Ȃ̂ŁA�`�|�a�{�b�|�c ���A
�}�P�P�A�}�Q�Q�A�E�E�E�@�ƂȂ邱�Ƃ͂Ȃ��̂ŁA�@�`�|�a�{�b�|�c���O�@�����A�@�`�{�b���a�{�c�@��
���邱�Ƃ��A�S���̐� �`�a�b�c ���P�P�̔{���ƂȂ邽�߂̏����ł���B
�@�Q�{�Q���S�{�O�@�̑g���������Ȃ��̂ŁA���߂�S���̐����́A
�@�Q�S�Q�O�A�Q�O�Q�S�A�S�Q�O�Q�@�̂R�ʂ�ł���B
���i�Q�j�́A�T���̃J�[�h����ׂĂł���T���̐��́A�T�I/�Q�I�|�S�I/�Q�I���S�W�i�ʂ�j�@����
�@�Ȃ��̂ŁA�l�ׂ��ɒ��ׂ邱�Ƃ��\�ł��邪�A���Ԃ������肷����̂ŁA�i�P�j�̕ʉ���
�@�悤�ɍl�����������낤�B
�i�Q�j�@�{��̏ꍇ�A�`�A�a�A�b�A�c �́A�O�A�Q�A�Q�A�S�A�U �̉��ꂩ�Ȃ̂ŁA�`�|�a�{�b�|�c ���A
�}�P�P�A�}�Q�Q�A�E�E�E�@�ƂȂ邱�Ƃ͂Ȃ��̂ŁA�@�`�|�a�{�b�|�c���O�@�����A�@�`�{�b���a�{�c�@��
���邱�Ƃ��A�S���̐� �`�a�b�c ���P�P�̔{���ƂȂ邽�߂̏����ł���B
�@�`�A�a�A�b�A�c ���A�U���܂܂Ȃ� �O�A�Q�A�Q�A�S �ō\�������Ƃ��A�S���̐��̂����A�P�P�Ŋ���
�����̂́A�i�P�j����A�R�ʂ肠��B
�@�`�A�a�A�b�A�c ���A�U���܂ނS�̐��ō\�������Ƃ��A�S���̐��̂����A�P�P�Ŋ����邽
�߂ɂ́A �U�{�O���S�{�Q�@�̑g���������Ȃ��̂ŁA���߂�S���̐����́A
�@�Q�O�S�U�A�Q�U�S�O�A�S�O�Q�U�A�S�U�Q�O�A�U�Q�O�S�A�U�S�O�Q�@�̂U�ʂ�ł���B
�ȏォ��A���߂�ꍇ�̐��́A�@�R�{�U���X�i�ʂ�j�@�@�i�I�j
��U���@�P�A�Q�A�R�A�S�A�T�A�U�A�V�A�W ����قȂ�S��I�ҁA�傫�������珇��A�AB�AC�AD �Ƃ�
�@�܂����B�܂��A�I�Ȃ������c��̂S����ёւ��AE�AF�AG�AH �Ƃ��܂����B����ƁA�S����
�@��ABCD����S���̐�DCBA�����������͂S���̐�EFGH�ł����B�S���̐�ABCD�����߂�B
�i���j�@��ӂ��A
�@�`�E�P�O�O�O�{�a�E�P�O�O�{�b�E�P�O�{�c�|�i�c�E�P�O�O�O�{�b�E�P�O�O�{�a�E�P�O�{�`�j
���d�E�P�O�O�O�{�e�E�P�O�O�{�f�E�P�O�{�g
���Ȃ킿�A�@�`�E�X�X�X�{�a�E�X�O�|�b�E�X�O�|�c�E�X�X�X���d�E�P�O�O�O�{�e�E�P�O�O�{�f�E�P�O�{�g
�@����āA�@�d�{�e�{�f�{�g�߂O�@�i������ �X�j�@�����藧�B
�����ŁA�@�`�{�a�{�b�{�c�{�d�{�e�{�f�{�g���P�{�Q�{�R�{�S�{�T�{�U�{�V�{�W���W�E�X/�Q���R�U
���Ȃ킿�A�@�`�{�a�{�b�{�c�{�d�{�e�{�f�{�g�߂O�@�i������ �X�j�@�Ȃ̂ŁA
�@�`�{�a�{�b�{�c�߂O�@�i������ �X�j�@�A�d�{�e�{�f�{�g�߂O�@�i������ �X�j�@�����藧�B
����āA�@�`���a���b���c�@�ɒ��ӂ��āA�N���蓾��ꍇ���l����ƁA
�i�`�C�a�C�b�C�c�j���i�W�C�V�C�Q�C�P�j�A�i�W�C�U�C�R�C�P�j�A�i�W�C�T�C�S�C�P�j�A�i�W�C�T�C�R�C�Q�j�A
�@�@�i�V�C�U�C�S�C�P�j�A�i�V�C�U�C�R�C�Q�j�A�i�V�C�T�C�S�C�Q�j�A�i�U�C�T�C�S�C�R�j
�@�����ɂ��āA���ۂɌv�Z���Ă݂āA
�@�W�V�Q�P�|�P�Q�V�W���V�S�S�R�i�s�K�j�@�A�W�U�R�P�|�P�R�U�W���V�Q�U�R�i�s�K�j�@�A
�@�W�T�S�P�|�P�S�T�W���V�O�W�R�i�s�K�j�@�A�W�T�R�Q�|�Q�R�T�W���U�P�V�S�i�K�j�@�A
�@�V�U�S�P�|�P�S�U�V���U�P�V�S�i�s�K�j�@�A�V�U�R�Q�|�Q�R�U�W���T�Q�U�S�i�s�K�j�@�A
�@�V�T�S�Q�|�Q�S�T�W���T�O�W�S�i�s�K�j�@�A�U�T�S�R�|�R�S�T�W���R�O�W�T�i�s�K�j
�@�ȏォ��A���߂�S���̐��́A�@�W�T�R�Q�@�@�i�I�j
��V���@���}�̂悤�ȁA�d�r�P�A�d���P�A�X�C�b�`�@�`�F�̂V���܂ޓd�C��H������
�@�܂��B�X�C�b�`�̃I���E�I�t�̎d���͑S���łP�Q�W�ʂ肠��A���̂����d�����_������悤��
�@�X�C�b�`�̃I���E�I�t�̎d���͑S���ʼn��ʂ肠��܂����B
�@�@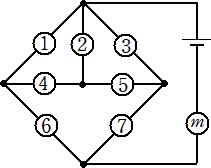
�i���j�@�d�����_�����Ȃ��ꍇ���l����B�ȉ��ŁA�X�C�b�`���n�m���u���v�A�n�e�e���u�~�v�ŕ\���B
�@�E���~�A�F���~�Ȃ�A�@�`�D�͔C�ӂȂ̂ŁA�N���蓾��ꍇ�́A�Q5���R�Q�i�ʂ�j
�@�E�����A�F���~�̂Ƃ��A
�@�@�@���~�A�C���~�Ȃ�A�A�A�B�A�D�͔C�ӂȂ̂ŁA�N���蓾��ꍇ�́A�Q3���W�i�ʂ�j
�@�@�@���~�A�C�����Ȃ�A�A���~�ŁA�B�܂��͇D���~�Ȃ̂ŁA
�@�@�N���蓾��ꍇ�́A�Q2�|�P���R�i�ʂ�j
�@�@����āA�N���蓾��ꍇ�̐��́A�@�W�{�R���P�P�i�ʂ�j
�@�E���~�A�F�����̂Ƃ��A��Ɠ��l�ɂ��āA�@�P�P�i�ʂ�j
�@�E�����A�F�����̂Ƃ��A
�@�@�@�ƇB�́~�ŁA�A���~�Ȃ�A�C�ƇD�͔C�ӂȂ̂ŁA�N���蓾��ꍇ�́A�Q2���S�i�ʂ�j
�@�@�@�ƇB�́~�ŁA�A�����Ȃ�A�C�ƇD�́~�Ȃ̂ŁA�N���蓾��ꍇ�́A�P�ʂ�
�@�@����āA�N���蓾��ꍇ�̐��́A�@�S�{�P���T�i�ʂ�j
���������āA�d�����_������悤�ȃX�C�b�`�̃I���E�I�t�̎d���͑S����
�@�P�Q�W�|�i�R�Q�{�P�P�~�Q�{�T�j���U�X�i�ʂ�j�@�@�i�I�j
��W���@���}�̂悤�ɁA��ABC�A��DEF������A�_A�AD�͂��ꂼ���EF�ABC��ɂ���܂��B
�@�܂��A��AB�ADE�͓_G�Ō����A��AC�ADF�͓_H�Ō����܂��B
�@AB��DE�AAC��DF�AAE��AF�@�ŁACD���R�EBD�ł��B�܂��ABC�aEF�ł��B
�@���̂Ƃ��A�l�p�`AGDH�̖ʐς́�AHF�̖ʐς̉��{�ł����B
�@�@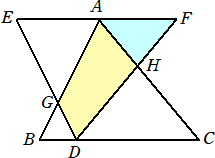
�i���j�@�_�`���ӂa�b�ɐ����`�o�������A�_�c���ӂd�e�ɐ����c�p�������B
�@�@
�@���̂Ƃ��A���`�a�o�߁��c�d�p�@�Ȃ̂ŁA�ڂa���ڂd�@�ƂȂ�B���l�ɂ��āA�ڂb���ڂe�@�Ȃ̂ŁA
���`�a�b�Ɓ��c�d�e�ɂ����āA�@�`�a���c�d�@�A�`�b���c�e�@�A�ڂa�`�b���ڂd�c�e�@�Ȃ̂ŁA
�Q�ӂƚ�p�����ɂ��A�@���`�a�b�߁��c�d�e�@�ł��邱�Ƃ�������B
�@���̂Ƃ��A�@�a�b���d�e�@�ł���̂ŁA�a�c���P �Ƃ���ƁA�c�b���R�ŁA�`�d���`�e���Q �ƂȂ�B
�@���`�g�e���r�@�Ƃ����ƁA�e�g �F �g�c���Q �F �R �Ȃ̂ŁA�@���`�c�g���i�R/�Q�j�r
�܂��A���`�c�d�����`�c�e���i�T/�Q�j�r�@�ŁA�d�f �F �f�c���Q �F �P �Ȃ̂ŁA�@���`�c�f���i�T/�U�j�r
�@����āA�l�p�`AGDH�̖ʐρ��i�R/�Q�j�r�{�i�T/�U�j�r���i�V/�R�j�r�@�ƂȂ�A
�@�l�p�`AGDH�̖ʐς́�AHF�̖ʐς̂V/�R�{�ł���B�@�@�i�I�j
��X���@�P�ӂ̒������Wcm�ł���Q�̐����`ABCD�APQRS������܂��B�����}�ɂ́A�_B
�@�𒆐S�Ƃ��_D��ʂ锼�~�ƁA�_C�𒆐S�Ƃ��_A��ʂ锼�~��������Ă��܂��B�E���}��
�@�悤�ɐ����`PQRS���@�̈ʒu����A�̈ʒu�܂Œ����A�̏�����ׂ邱�ƂȂ��]����Ƃ�
�@�ɕ�PQ���ʉ߂��鉩�F�����̖ʐςƁA�����}�̉��F�����̖ʐς̘a�����߂�B
| �@ |
 |
�@ |
 |
�i���j�@�Q�̐}�`����ɂ܂Ƃ߁A�ʐς̓�������������ꂩ����ƁA���߂�ʐς̘a��
�@�@���}�̉��F�����̖ʐςƂȂ�B
�@�@
�@����āA
�@�o�i�P/�S�j�i�W �j2�|�i�P/�S�j�E�U�S�p�~�Q�{�i�P/�W�j�i�W
�j2�|�i�P/�S�j�E�U�S�p�~�Q�{�i�P/�W�j�i�W �j2�~�Q
�j2�~�Q
���R�Q�{�R�Q���U�S��
�@���R�D�P�S�@�Ƃ��āA�@�U�S���Q�O�O�D�X�U�i����2�j�@�@�i�I�j
��P�O���@���}�̌܊p�`ABCDE�͐��܊p�`�ŁA�l�p�` CDFG�AADH�h �͂ǂ���������`��
�@���B���̂Ƃ��A�p�Ƃ̑傫�������߂�B
�@�@
�i���j�@���}�̂悤�ɕ⏕���������B
�@�@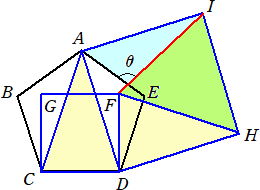
�@���܊p�`�̓��p�̑傫���́A�@�P�W�O���~�R���T���P�O�W���Ȃ̂ŁA�@�ڂb�`�c���R�U��
�@���b�`�c�A���e�g�c�͂Q���ӎO�p�`�ŁA���b�`�c�߁��e�g�c���A�@�ڂe�g�c���R�U��
�@����āA�@�ڂe�g�h���T�S���ƂȂ�B
�@���e�g�h �͂e�g���g�h �̂Q���ӎO�p�`�Ȃ̂ŁA�@�ڂg�h�e���U�R���@�ł���B
�@����āA�@�ڂ`�h�e���Q�V���@�ƂȂ�B
�Ƃ���ŁA�@�ڂh�`�d���X�O���|�R�U�����T�S���@�Ȃ̂ŁA
�@�Ɓ��P�W�O���|�i�Q�V���{�T�S���j���X�X���@�@�i�I�j
��P�P���@���}�̒�����ABCD-EFGH�ɂ��āA��AD�AAE�AEF�̒����͂��ꂼ�� �Pcm�A
�@�Qcm�A�Pcm �ł��B�܂��A�_ I �͕�CD�̐^�̓_�ł��B�R�_A�AF�A�h ��ʂ镽�ʂŁA��
�@�̒����̂�蕪�����Ƃ��A�_C���܂ޕ��̗��̂̑̐ς́A�����̗��̂̑̐ς̉�
�@�{�ł����B
�@�@
�i���j�@��������Ԃɐ}�`�ߍ��ނƁA
�@�@
�@�R�_�`�i�P�C�O�C�Q�j�A�e�i�P�C�P�C�O�j�A�h�i�O�C�P/�Q�C�Q�j��ʂ镽�ʂ̕�������
�@�����{�����{�����{�����O�@�i���A���A���̉��ꂩ�͂O�łȂ��j
�Ƃ����ƁA�@���{�Q���{�����O�@�A���{���{�����O�@�A�i�P/�Q�j���{�Q���{�����O
������A�@���|�Q�����O�@���Ȃ킿�A�@�����Q���@�ŁA�@�R���{�����O�@���A�@�����|�i�P/�R�j��
����āA�@�����|�i�Q/�R�j���@�ƂȂ�A�@�����|�i�P/�R�j��
���̂Ƃ��A�|�i�P/�R�j�����|�i�Q/�R�j�����|�i�P/�R�j�����{�����O�@�ƂȂ�A���ӂ��|�i�P/�R�j�� �Ŋ�����
�@���{�Q���{���|�R���O
�@���̕��ʂ́A�e���ƁA�i�R�C�O�C�O�j�A�i�O�C�R/�Q�C�O�j�A�i�O�C�O�C�R�j�@�Ō����B
���̂R�_�Ɠ_�g�ō����O�p���̑̐ς́A�@�R�E�i�R/�Q�j�E�i�P/�Q�j�E�R�E�i�P/�R�j���X/�S
���̑̐ς���A���F�����̂R�̎O�p���̑̐ς����������A�_C���܂܂Ȃ����̗��̂�
�̐ς����߂���B���Ȃ킿�A�����O�A�����P �̂Ƃ��A�����P �ɒ��ӂ��āA
�X/�S�|�Q�E�P�E�i�P/�Q�j�E�Q�E�i�P/�R�j�|�P�E�i�P/�Q�j�E�i�P/�Q�j�E�P�E�i�P/�R�j�|�P�E�i�P/�Q�j�E�i�P/�Q�j�E�P�E�i�P/�R�j
���X/�S�|�Q/�R�|�P/�P�Q�|�P/�P�Q���P�V/�P�Q
�@�����ŁA�����̂̑̐ς́A�@�P�E�P�E�Q���Q�@�Ȃ̂ŁA�_C���܂ޕ��̗��̂̑̐ς́A
�@�Q�|�i�P�V/�P�Q�j���V/�P�Q
�@�ȏォ��A�_C���܂ޕ��̗��̂̑̐ς́A�����̗��̂̑̐ς�
�@�i�V/�P�Q�j���i�P�V/�P�Q�j���V/�P�V�i�{�j�@�ł���B�@�@�i�I�j
�i�R�����g�j�@���̂��A���� �����P �Őؒf����ƁA�Z���I�ȉ�@���ł������ł���B
�i�ʉ��j
�@�@
�@�P�ӂ��P�̗����̂��c�ɂQ�ς܂�Ă���ƍl����B���̗��̂��A�R�_A�AF�A�h ��ʂ镽��
�ł�����Ƃ��A��̒i�̗����̂́A���̐ςQ�̗��̂ɕ�������A���̒i�̗�����
�́A�O�p���Ƒ��̗��̂ɕ��������B
�@����āA�_C���܂ޕ��̗��̂̑̐ς́A
�@�P/�Q�{�i�P/�Q�j�E�P�E�i�P/�Q�j�E�P�E�i�P/�R�j���P/�Q�{�P/�P�Q���V/�P�Q
�@�����̂̑̐ς́A�@�P�E�P�E�Q���Q�@�Ȃ̂ŁA�_C���܂܂Ȃ����̗��̂̑̐ς́A
�@�Q�|�V/�P�Q���P�V/�P�Q
����āA�_C���܂ޕ��̗��̂̑̐ς́A�����̗��̂̑̐ς�
�@�i�V/�P�Q�j���i�P�V/�P�Q�j���V/�P�V�i�{�j�@�ł���B�@�@�i�I�j
��P�Q���@���闧�̂̓W�J�}�͉��}�̂悤�ɂȂ��Ă��܂��B���̗��̂̑̐ς����߂�B
�@�������A�����L���������ꂽ�ӂ̒����͓������Ƃ��܂��B
�@�@
�i���j�@�W�J�}�����Ƃɂ��Ƃ̗��̂�����ƁA
�@�@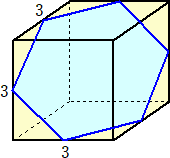
�@���Z�p�`�������̂̊e�ӂ̒��_������œ����邱�Ƃ���
�@���߂�̐ς́A�@�R�~�R�~�R���Q���P�R�D�T�@�@�i�I�j
�i�Q���ځj
��P���@�P�O�ȏ�̐����ɑ��āA�e�ʂ̐����������킹�鑀��P����L�����ɂ��\����
�@���B���̑�����J��Ԃ��A�P�O��菬�����Ȃ�ƏI�����܂��B
�i�P�j�@�Q���̐���A�ŁAA���O �ƂȂ���̂͑S���ʼn����邩�B�R���̐���B�ŁAB���O �ƂȂ�
�@���̂͑S���ʼn����邩�B
�i�Q�j�@�R���̐���C�ŁAC��D���Q �ƂȂ���̂��l���܂��B�������AD�͐����ł��B
(�A)�@���̂悤�Ȑ����b�̂����A�ł����������̂ƍł��傫�����̂����߂�B
(�C)�@���̂悤�Ȑ����b�͑S���ʼn�����܂����B
�i���j�i�P�j�@�Q���̐���A�ŁAA���O �ƂȂ���̂́A�u*�O�v�̃^�C�v�ŁA*���P�`�X �̂X�ʂ�
�@�R���̐���B�ŁAB���O �ƂȂ���̂́A�u*�O�O�`*�O�X�v�̃^�C�v�ŁA*���P�`�X �̂X�O�ʂ�
�@�܂��́A�u*�P�O�`*�X�O�v�̃^�C�v�ŁA*���P�`�X �̂W�P�ʂ�@�ŁA�v�X�O�{�W�P���P�V�P�i�ʂ�j
�i�Q�j�i�A�j �c�̉\���́A
�@�P�Q�@�A�Q�P�@�A�P�P�Q�@�A�P�Q�P�@�A�Q�P�P�@�A�P�P�P�Q�@�A�P�P�Q�P�@�A�P�Q�P�P�@�A�Q�P�P�P�@�A�E�E�E
�ł��邪�A�P�P�P�Q���Q�E�Q�E�Q�E�P�R�X�@�A�P�P�Q�P���P�X�E�T�X�@�A�P�Q�P�P���V�E�P�V�R�@�A�Q�P�P�P�i�f���j
�Ȃ̂ŁA�b���R���̐����Ƃ������Ƃ���A�N���肦�Ȃ��B
�P�P�Q���Q�E�Q�E�Q�E�Q�E�V���Q�E�W�E�V���S�E�S�E�V�@���A
�@�Q�V�W�A�Q�W�V�A�V�Q�W�A�V�W�Q�A�W�Q�V�A�W�V�Q�A�S�S�V�A�S�V�S�A�V�S�S
�P�Q�P���P�P�E�P�P�@���A�Y������b�͑��݂��Ȃ��B
�Q�P�P�i�f���j�@���A�Y������b�͑��݂��Ȃ��B
�P�Q���Q�E�Q�E�R���P�E�Q�E�U���P�E�R�E�S�@���A
�@�P�Q�U�A�P�U�Q�A�Q�P�U�A�Q�U�Q�A�U�P�Q�A�U�Q�P�A�Q�Q�R�A�Q�R�Q�A�R�Q�Q�A�P�R�S�A�P�S�R�A�R�P�S�A�R�S�P�A
�@�S�P�R�A�S�R�P
�Q�P���P�E�R�E�V�@���A�@�P�R�V�A�P�V�R�A�R�P�V�A�R�V�P�A�V�P�R�A�V�R�P
�@�ȏォ��A�Y�����鐮���b�ōł����������̂́A�P�Q�U�@�ŁA�ł��傫�����̂́A�W�V�Q
�i�C�j�@�i�A�j�̌v�Z����A�����b�̋N���蓾��\���́A
�@�Q�V�W�A�Q�W�V�A�V�Q�W�A�V�W�Q�A�W�Q�V�A�W�V�Q�A�S�S�V�A�S�V�S�A�V�S�S�A�P�Q�U�A�P�U�Q�A�Q�P�U�A�Q�U�Q�A
�@�U�P�Q�A�U�Q�P�A�Q�Q�R�A�Q�R�Q�A�R�Q�Q�A�P�R�S�A�P�S�R�A�R�P�S�A�R�S�P�A�S�P�R�A�S�R�P�A�P�R�V�A�P�V�R�A
�@�R�P�V�A�R�V�P�A�V�P�R�A�V�R�P
�@�ȏ�́@�R�O�ʂ肠��B�@�@�i�I�j
��Q���@���iP�́A�P���ɂ��A�H��A�łQ�O�O�O�A�H��B�łR�O�O�O���Y����܂��B�H��A
�@�Ő��Y���ꂽ���iP����P�O�O�O���o���Č�������ƂV�s�Ǖi��������܂��B�܂��A
�@�H��B�Ő��Y���ꂽ���iP����P�O�O�O���o���Č�������ƂP�Q�s�Ǖi���������
�@���B�H��A�ƍH��B�Ő��Y���ꂽ���iP�͂��ׂČ�����ɓ��ׂ���A�����̑O�ɂ悭����
�@���܂��B
�@���Ƃ��A�H��A�Ő��Y���ꂽ���iP���R�O�O�O�������Ƃ��A���̒��̕s�Ǖi�̌���
�R�O�O�O�~�i�V/�P�O�O�O�j���Q�P�i�j�Ɛ�������܂��B���ۂɂ́A�Q�P��葽�����Ƃ����Ȃ���
�Ƃ����蓾�܂����A���̂悤�ɐ������܂��B���̗�ɂȂ���āA���̖₢�ɓ����Ȃ����B
�i�P�j�@������ԁA�H��A�A�H��B�͂ǂ�����x�܂��ғ����܂����B���̊��ԂɌ�����ɓ���
�@���ꂽ���iP����s�Ǖi���P�O�O�O���������Ƃ��A���̂P�O�O�O�̕s�Ǖi�̂����H��A
�@�Ő��Y���ꂽ�s�Ǖi�̌��𐄑�����B
�i�Q�j�@����N�̂S���A�H��A�͋x�܂��ғ����܂������A�H��B�͉������x�ƂƂȂ�܂����B��
�@�̂P�P���Ɍ�����ɓ��ׂ��ꂽ���iP����P�O�O�O�O���o���Č��������Ƃ���A�s�Ǖi
�@���W�O������܂����B���̂W�O�̕s�Ǖi�̂����H��A�Ő��Y���ꂽ�s�Ǖi�̌���
�@���Ɛ�������܂����B
�i���j�i�P�j�@�H��A�łQ�O�O�O�A�H��B�łR�O�O�O���Y����ƁA�s�Ǖi�̌��́A
�@�@�Q�O�O�O�~�i�V/�P�O�O�O�j�{�R�O�O�O�~�i�P�Q/�P�O�O�O�j���P�S�{�R�U���T�O�i�j
�@�s�Ǖi�̌����P�O�O�O�Ȃ̂ŁA���̂P�O�O�O�̕s�Ǖi�̂����H��A�Ő��Y���ꂽ�s��
�i�̌��́A�@�P�O�O�O�~�i�P�S/�T�O�j���Q�W�O�i�j
�i�Q�j�@�P�O�O�O�O�̂����A�H��A�Ő��Y���ꂽ���iP�̌��� �� �Ƃ���ƁA��ӂ��A
�@���E�i�V/�P�O�O�O�j�{�i�P�O�O�O�O�| �� �j�E�i�P�Q/�P�O�O�O�j���W�O
������A�@�V���{�P�Q�O�O�O�O�|�P�Q�����W�O�O�O�O�@�Ȃ̂ŁA�@�T�����S�O�O�O�O�@���A�@�����W�O�O�O
����āA�W�O�̕s�Ǖi�̂����H��A�Ő��Y���ꂽ�s�Ǖi�̌��́A
�@�W�O�O�O�~�i�V/�P�O�O�O�j���T�U�i�j�@�@�i�I�j
��R���@�i�P�j�@���}�̐����`ABCD�ɂ����āA��AEF�̖ʐς����߂�B�܂��A�S�̖ʂ���
�@�ꂼ�ꁢ�`�a�d�A���d�b�e�A���e�c�`�A���`�d�e�ƍ����ȎO�p���̑̐ς����߂�B
�@�@
�i�Q�j�@���}�̂悤�ȁA�P�ӂ̒������Q�Ocm�̗����� GHIJ-KLMN ������܂��B�_P��GP�̒�
�@�����P�Ocm�ƂȂ��GJ��̓_�A�_Q��GQ�̒������P�Tcm �ƂȂ��GH��̓_�A�_R��KR��
�@�������Rcm�ƂȂ��KL��̓_�ł��B
�@�@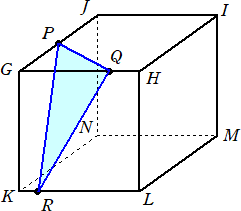
(�A)�@�R�_�o�A�p�A�q��ʂ镽�ʂƕ�KN�������_��S�Ƃ��܂��B���̂Ƃ��AKS�̒��������߂�B
�@�܂��A�R�_P�AQ�AR��ʂ镽�ʂŗ�����GHIJ-KLMN���Q�̗��̂ɐ蕪�����Ƃ��AG����
�ޕ��̗��̂̑̐ς����߂�B
(�C)�@�S�_G�AP�AQ�AR�_�Ƃ���O�p���́A��PQR���ʂƂ݂��Ƃ��̍��������߂�B
�@�@
(�E)�@�S�_M�AP�AQ�AR�_�Ƃ���O�p���́A��PQR���ʂƂ݂��Ƃ��̍��������߂�B
�@�@
�i���j�i�P�j�@���`�d�e
�@�@���Q�T�|�R�E�T�E�i�P/�Q�j�|�Q�E�R�E�i�P/�Q�j�|�Q�E�T�E�i�P/�Q�j���Q�T�|�R�P/�Q���P�X/�Q�i����2�j
�@���߂�O�p���́A
�@�@
�Ȃ̂ŁA�̐ς́A�@�T�~�R�~�i�P/�Q�j�~�Q�~�i�P/�R�j���T�i����3�j
�i�Q�j�i�A�j�@�o�p�a�r�q�@�Ȃ̂ŁA�@�j�r/�R���P�O/�P�T���Q/�R�@���A�@�j�r���Q�i�����j
�@���f�o�p���ʂƂ���O�p���̍������́A�@�i���|�Q�O�j �F �R���� �F �P�T�@���A�����Q�T
�@����āA���߂�̐ς́A
�@�P�O�E�P�T�E�i�P/�Q�j�E�Q�T�E�i�P/�R�j�|�Q�E�R�E�i�P/�Q�j�E�T�E�i�P/�R�j���U�Q�O�i����3�j
�i�C�j�@�i�A�j���A�f�j�̉�����ɁA�f�s���Q�T�@�ƂȂ�_�s���Ƃ�B
�@�@
�@�Ԑ��̎O�p���́A�i�P�j�ōl�����O�p���ŁA�@���s�r�q���P�X/�Q�@�ł���B
���s�r�q�䁢�s�o�p�@�ő����䂪 �P �F �T �ł��邱�Ƃ���A�@���s�o�p���i�P�X/�Q�j�~�Q�T���S�V�T/�Q
���߂鍂���� �� �Ƃ����ƁA�O�p���s-�f�o�p�̑̐ςɒ��ڂ��āA
�@�i�S�V�T/�Q�j�~���~�i�P/�R�j���P�O�E�P�T�E�i�P/�Q�j�E�Q�T�E�i�P/�R�j�@���A
�@�����P�O�E�P�T�E�Q�T/�S�V�T���P�T�O/�P�X�i�����j
�i�R�����g�j�@�����A���̂悤�Ɍv�Z�����B
�@�f�i�O�C�O�C�O�j�A�o�i�P�O�C�O�C�O�j�A�p�i�O�C�P�T�C�O�j�A�q�i�O�C�R�C�Q�O�j�Ƃ��āA
�R�_�o�A�p�A�q��ʂ镽�ʂ̕������́A�@�i�P/�Q�j���{�i�P/�R�j���{�i�P/�T�j���|�T���O�@�ƂȂ�̂ŁA
�f�i�O�C�O�C�O�j�ƕ��ʂ̋����́A�@�T/��o�i�P/�Q�j2�{�i�P/�R�j2�{�i�P/�T�j2�p���P�T�O/�P�X
���U�������Ă͂����Ȃ��ł��ˁD�D�D�B
�i�E�j�@�i�P�j�Ɠ��l�ɂ��āA
�@���l�r�q���S�O�O�|�P�W�E�Q�O�E�i�P/�Q�j�|�P�V�E�Q�O�E�i�P/�Q�j�|�Q�E�R�E�i�P/�Q�j���S�V
�Ȃ̂ŁA���߂鍂���� �� �Ƃ����ƁA�O�p���s-�r�q�l�̑̐ςɒ��ڂ��āA
�@�i�P�X/�Q�j�~���~�i�P/�R�j���S�V�~�T�~�i�P/�R�j�@���A�@�����S�V�O/�P�X�@�@�i�I�j
��S���@�i�P�j�@���}�̂悤�Ȓ����`ABCD������A��BC��ɓ_E�A��CD��ɓ_F������܂��B
�@���`�d�e�����p���O�p�`�ł���Ƃ��A��AEF�̖ʐς����߂�B
�@�@
�i�Q�j�@�P�ӂ̒������P�Qcm�ł��鐳���`GHIJ������܂��B���}�̂悤�ɁA��HI �̉������
�@�_K������AGK��I�i���_ L�Ō�����Ă��܂��B�܂��A���オ�Rcm�ł��锼�~����GJL��
�@�҂�������܂��Ă��܂��B���̂Ƃ��A��GHK�ɂ҂�������܂�~�̔��a�ƕ�HK�̒�������
�@�߂�B
�@�@
�i���j�i�P�j�@��ӂ��A���`�d�e�́A�ڂ`�d�e���X�O���A�`�d���e�d�@�̒��p�Q���ӎO�p�`�ł���B
����āA���`�a�d�߁��d�b�e�@���A�b�d���S�A�d�a���P�@�ƂȂ�B
�@���̂Ƃ��A�@�`�d2���S2�{�P2���P�V�@�Ȃ̂ŁA�@���`�d�e���`�d2�E�i�P/�Q�j���P�V/�Q
�i�ʉ��j�@�e�b���P�A�c�e���R�@�Ȃ̂ŁA
�@���`�d�e���Q�O�|�P�T/�Q�|�Q�~�Q���P�V/�Q
�i�Q�j �~�O�̂P�_����~�Ɉ������ڐ��̒����͓������A���̓_�Ɖ~�̒��S�����Ԑ����́A�Q��
�@���̂Ȃ��p���Q��������B
�@�@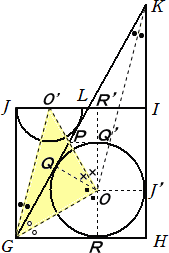
�@����āA�ڂn�f�n�f���S�T����������B�܂��A�ڂf�n�o���X�O���Ȃ̂ŁA���f�n�n�f�́A�����`
�f�q�q�f�i���̒��p�Q���ӎO�p�`�ƂȂ�B�i�P�j�Ɠ��l�ɍl���āA
�@�q�n�{�q�f�n���P�Q�A�f�q���q�f�n�A�q�n���q�f�n�f�A�f�q���q�f�n�f�{�R�@���A
�@�q�f�n���f�q���q�f�n�f�{�R���q�n�{�R�@�Ȃ̂ŁA�@�Q�q�n�{�R���P�Q�@���A�@�q�n���X/�Q
�ȏォ��A��GHK�ɂ҂�������܂�~�̔��a�́A�X/�Q�i�����j�ł���B
���̂Ƃ��A���j�n�i�f�䁢�f�n�f�i�@���A�j�i�f �F �n�i�f���f�i �F �n�f�i�@���Ȃ킿�A
�@�j�i�f �F �X/�Q���P�Q �F �R���S �F �P�@���A�@�j�i�f���P�W
�@�ȏォ��A�@�g�j���P�W�{�X/�Q���S�T/�Q�i�����j�@�@�i�I�j
�i�R�����g�j�@�i�P�j�̃q���g�̏o�������S�����ł��ˁI�i�Q�j�ɒ��ڌ����Ă��܂��B
��T���@���}�̂悤�ȓI������AA���� I �̂X�̏ꏊ�ɁA�P�A�Q�A�R�A�S�A�T�A�U�A�V�A�W�A�X ��
�@�X�̐����P��������Ă��܂��B�܂��A�������͂Q�ȏ�̏ꏊ�ɏ�����邱�Ƃ͂�
�@��܂���B
�@�@
�i�P�j�@���Y���|�[�����R������ƁAA�AE�A�h �ɓ�����A���������ꏊ�ɏ����ꂽ���̘a
�@�͂P�O�ɂȂ�܂����B���Y������|�[�����R������ƁAC�AE�AG �ɓ�����A���������ꏊ��
�@�����ꂽ���̘a�͂P�O�ɂȂ�܂����B
(�A)�@E�ɏ����ꂽ�����T�ł���Ƃ��A�I�ɏ����ꂽ�X�̐��̕��т͑S���ʼn��ʂ肠��܂����B
(�C)�@�I�ɏ����ꂽ�X�̐��̕��҂́A(�A)�̏ꍇ���܂߂đS���ʼn��ʂ肠��܂����B
�i�Q�j�@���Y���{�[�����R������ƁA�I�̂ǂ̏c��ɂ��P�A�ǂ̉���ɂ��P��
�@������A���������ꏊ�ɏ����ꂽ���̘a�͂P�O�ɂȂ�܂����B���Y������|�[�����R����
�@��ƁA�I�̂ǂ̏c��ɂ��P�A�ǂ̉���ɂ��P������A���������ꏊ�ɏ����ꂽ
�@���̘a�͂P�O�ɂȂ�܂����B�܂��A���Y�����ĂĎ��Y�����ĂȂ������ꏊ������܂�
�@���B���̂Ƃ��A�I�ɏ����ꂽ�X�̐��̕��҂́A�i�P�j�̏ꍇ���܂߂đS���ʼn��ʂ肠��܂�
�@���B
�i���j�i�P�j�i�A�j�@�d���T ���A�`�{�h���T �ƂȂ�i�`�C�h�j�̑g�́A
�@�i�P�C�S�j�A�i�Q�C�R�j�A�i�R�C�Q�j�A�i�S�C�P�j�@�̂S�ʂ�ŁA���̂����̂P�ʂ�A
�Ⴆ�A�i�`�C�h�j���i�P�C�S�j�ɑ��āA�i�b�C�f�j���i�Q�C�R�j�A�i�R�C�Q�j�@�̂Q�ʂ�ŁA���̂����̂P�ʂ�A
�Ⴆ�A�i�b�C�f�j���i�Q�C�R�j�ɑ��āA�c��̂a�A�c�A�e�A�g�ɁA�T�A�U�A�V�A�W ������U��悢�B
�@����āA���߂�ꍇ�̐��́A�@�S�~�Q�~�S�I���P�X�Q�i�ʂ�j
�i�C�j�@�d���P �̂Ƃ��A�`�{�h���X �ƂȂ�i�`�C�h�j�̑g�́A
�@�i�Q�C�V�j�A�i�R�C�U�j�A�i�S�C�T�j�A�i�T�C�S�j�A�i�U�C�R�j�A�i�V�C�Q�j�@�̂U�ʂ�ŁA���̂����̂P�ʂ�A
�Ⴆ�A�i�`�C�h�j���i�Q�C�V�j�ɑ��āA�i�b�C�f�j���i�R�C�U�j�A�i�S�C�T�j�A�i�T�C�S�j�A�i�U�C�R�j�@�̂S�ʂ�
�ŁA���̂����̂P�ʂ�A�Ⴆ�A�i�b�C�f�j���i�R�C�U�j�ɑ��āA�c��̂a�A�c�A�e�A�g�ɁA�S�A�T�A�W�A�X
������U��悢�B���̂Ƃ��̏ꍇ�̐��́A�@�U�~�S�~�S�I���T�V�U�i�ʂ�j
�@�d���Q �̂Ƃ��A�`�{�h���W �ƂȂ�i�`�C�h�j�̑g�́A
�@�i�P�C�V�j�A�i�R�C�T�j�A�i�T�C�R�j�A�i�V�C�P�j�@�̂S�ʂ�ŁA���̂����̂P�ʂ�A
�Ⴆ�A�i�`�C�h�j���i�P�C�V�j�ɑ��āA�i�b�C�f�j���i�R�C�T�j�A�i�T�C�R�j�@�̂Q�ʂ�
�ŁA���̂����̂P�ʂ�A�Ⴆ�A�i�b�C�f�j���i�R�C�T�j�ɑ��āA�c��̂a�A�c�A�e�A�g�ɁA�S�A�U�A�W�A�X
������U��悢�B���̂Ƃ��̏ꍇ�̐��́A�@�S�~�Q�~�S�I���P�X�Q�i�ʂ�j
�@�d���R �̂Ƃ��A�`�{�h���V �ƂȂ�i�`�C�h�j�̑g�́A
�@�i�P�C�U�j�A�i�Q�C�T�j�A�i�T�C�Q�j�A�i�U�C�P�j�@�̂S�ʂ�ŁA���̂����̂P�ʂ�A
�Ⴆ�A�i�`�C�h�j���i�P�C�U�j�ɑ��āA�i�b�C�f�j���i�Q�C�T�j�A�i�T�C�Q�j�@�̂Q�ʂ�
�ŁA���̂����̂P�ʂ�A�Ⴆ�A�i�b�C�f�j���i�Q�C�T�j�ɑ��āA�c��̂a�A�c�A�e�A�g�ɁA�S�A�V�A�W�A�X
������U��悢�B���̂Ƃ��̏ꍇ�̐��́A�@�S�~�Q�~�S�I���P�X�Q�i�ʂ�j
�@�d���S �̂Ƃ��A�`�{�h���U �ƂȂ�i�`�C�h�j�̑g�́A
�@�i�P�C�T�j�A�i�T�C�P�j�@�̂Q�ʂ�ŁA�i�b�C�f�j�ɓ��Ă͂܂���̂��Ȃ��̂ŁA���̏ꍇ�͋N����Ȃ��B
�@�d���T �̂Ƃ��A�i�A�j����A�ꍇ�̐��́A�@�P�X�Q�ʂ�
�@�d���U �̂Ƃ��A�`�{�h���S �ƂȂ�i�`�C�h�j�̑g�́A
�@�i�P�C�R�j�A�i�R�C�P�j�@�̂Q�ʂ�ŁA�i�b�C�f�j�ɓ��Ă͂܂���̂��Ȃ��̂ŁA���̏ꍇ�͋N����Ȃ��B
�@�d���V �̂Ƃ��A�`�{�h���R �ƂȂ�i�`�C�h�j�̑g�́A
�@�i�P�C�Q�j�A�i�Q�C�P�j�@�̂Q�ʂ�ŁA�i�b�C�f�j�ɓ��Ă͂܂���̂��Ȃ��̂ŁA���̏ꍇ�͋N����Ȃ��B
�@�d���W �̂Ƃ��A�`�{�h���Q �ƂȂ�i�`�C�h�j�̑g�͑��݂��Ȃ��̂ŁA���̏ꍇ�͋N����Ȃ��B
�@�d���X �̂Ƃ��A�`�{�h���P �ƂȂ�i�`�C�h�j�̑g�͑��݂��Ȃ��̂ŁA���̏ꍇ�͋N����Ȃ��B
�ȏォ��A���߂�ꍇ�̐��́A�@�T�V�U�{�P�X�Q�~�R���P�P�T�Q�i�ʂ�j
�i�Q�j�@�R�̐��̘a���P�O�ɂȂ�ꍇ�́A�i�P�C�Q�C�V�j�A�i�P�C�R�C�U�j�A�i�P�C�S�C�T�j�A�i�Q�C�R�C�T�j
�����́A�݂��ɂP�̐������L���Ă���̂ŁA�u���Y�����ĂĎ��Y�����ĂȂ�����
�ꏊ������܂����v�Ƃ̂��Ƃ���A�i�P�j�̂悤�ɁA���Y����Ǝ��Y���������Ă��Ƃ��낪
�P���������āA�c��̓o���o���ɓ��������Ƃ������Ƃł���B����ƁA�S�̃t���[�X�y�[�X��
�o����̂ŁA���ߕ��́i�P�j�ƑS�����l�ł���B
�@���Y����Ǝ��Y���������Ă��Ƃ���̏ꍇ�͂X�ʂ�ŁA���̂����̂P�ʂ�ɑ��āA
�I�ɏ����ꂽ�X�̐��̕��т͑S���łP�P�T�Q�ʂ肠�邱�Ƃ���A���߂�ꍇ�̐��́A
�@�X�~�P�P�T�Q���P�O�R�U�W�i�ʂ�j�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�P���Q�X���t��
�@�ߘa�V�N�x�咆�w�̓����́A�P���P�W���E�P�X���̗����s��ꂽ�B�P���ځE�Q���ڂƂQ����
�s��ꂽ�B�i�P���ځj�͑������m�ɏ����ł���́A�i�Q���ځj�͊m���Ș_�ؗ͂�������ŁA
�Z���ɋ������w�����W�߂����Ƃ����w�Z�̎v�f���\�����ݎ���������ƂȂ��Ă���B
�������ʔ��������A���ɂȂ�������ʼn����Ă݂��B���͈ꕔ���肳��Ă���B
�i�P���ځj
��Q���@�@�e��A�ɐH�������P�O�O���A�e��B�ɔZ�x�T�D�S���̐H�������R�O�������Ă���B�e��
�@�@A����V�O���̐H������e��B�Ɉڂ��Ă悭�������������ƁA�e��B����T�O���̐H������e
�@�@��A�Ɉڂ��Ă悭�����������Ƃ���A�e��A�̐H�����̔Z�x���W���ɂȂ����B
�@�e��A�̐H�����̔Z�x�͍ŏ������炾�������H
�i���j�@�e��A�̐H�����̍ŏ��̔Z�x�������Ƃ���B�H���̗ʂɒ��ڂ��čl����B
�@�`���a�̑����̂a�̐H���ʂ́A�V�O�E�i��/�P�O�O�j�{�R�O�E�i�T�D�S/�P�O�O�j���O�D�V���{�P�D�U�Q
�@�a���`�̑����̂`�̐H���ʂ́A
�@�O�D�R���{�i�O�D�V���{�P�D�U�Q�j�E�i�T�O/�P�O�O�j���O�D�U�T���{�O�D�W�P
���������āA�Z�x�́A�@�i�O�D�U�T���{�O�D�W�P�j���W�O�~�P�O�O���W�@���A�@�O�D�U�T�����T�D�T�X
�@���Ȃ킿�A�@�����W�D�U�@���A�e��A�̐H�����̔Z�x�͍ŏ� �W�D�U���ł������B�@�@�i�I�j
��R���@�@���i�̒艿����d����l�ƌo����������������z�����v�ł���B�ȉ��ł́A��
�@�@���A�d����l�A�o��A���v�͂��ׂ�1������̂��̂��l����B
�@�Q�O�Q�Q�N�̏��i�̒艿�͂P�O�O�O�~�ŁA�Q�O�Q�R�N���艿�͂P�O�O�O�~���������A�d����l��
�Q�O�Q�Q�N���Q�������Ȃ�A�o��͕ς��Ȃ��������߁A���v���Q�O�Q�Q�N�̂U�W���ɂȂ����B
�Q�O�Q�S�N�͎d����l�͂Q�O�Q�R�N�ƕς��Ȃ��������A�o��Q�O�Q�R�N���S�������Ȃ�����
�ŁA���v���Q�O�Q�Q�N�Ɠ����ɂ��邽�߂ɏ��i�̒艿���Q�Q�O�~���������B
�@�Q�O�Q�Q�N�̗��v�͂����炩�B
�i���j�@�Q�O�Q�Q�N�̏��i�̎d����l�A�o��A���v�����ꂼ�� ���A���A�� �Ƃ����ƁA��ӂ��A
�@���{���{�����P�O�O�O�@�E�E�E�@�i�P�j
�@�P�D�Q���{���{�O�D�U�W�����P�O�O�O�@�E�E�E�@�i�Q�j
�@�P�D�Q���{�P�D�S���{�����P�Q�Q�O�@�E�E�E�@�i�R�j
�i�Q�j�|�i�P�j�@���A�@�O�D�Q���|�O�D�R�Q�����O�@���Ȃ킿�A�@�����P�D�U��
�i�R�j�|�i�Q�j�@���A�@�O�D�S���{�O�D�R�Q�����Q�Q�O�@���Ȃ킿�A�@�����T�T�O�|�O�D�W��
�������i�P�j�ɑ�����āA�@�P�D�U���{�T�T�O�|�O�D�W���{�����P�O�O�O�@���A�@�P�D�W�����S�T�O
�@����āA�@�����Q�T�O�@���A���߂闘�v�́A�Q�T�O�~�@�@�i�I�j
�i�R�����g�j�@�R���A���ꎟ�������̉�@�́A���w�ł͏펯�Ȃ̂��낤���H
��S���@�@�Q�O�Q�T�͂X�̔{���ł��Q�T�̔{���ł�����A�S�̈ʂ̐��̂����P�������O�ł���B
�@�@�S���̐����̂����A�X�̔{���ł��Q�T�̔{���ł�����A�S�̈ʂ̐��̂����P�������O�ł�
�@�@����̂́A�Q�O�Q�T���܂߂đS���ʼn��ʂ肠�邩�B
�i���j�@�O�̏ꏊ�ɒ��ڂ��ďꍇ�ɕ�����B
*�O** �̂Ƃ��A�Q�T�̔{���ɂȂ邽�߂ɂ́A*�O�Q�T�A*�O�V�T
�@�e�ʂ̐��̘a���X�̔{���ł���悢�̂ŁA���߂鐔�́A�@�Q�O�Q�T�A�U�O�V�T
**�O* �̂Ƃ��A�Q�T�̔{���͑��݂��Ȃ��B
***�O �̂Ƃ��A�Q�T�̔{���ɂȂ邽�߂ɂ́A**�T�O�@���X�̔{���ł���悢�B
�@�e�ʂ̐��̘a���X�̔{���ł���悢�̂ŁA���߂鐔�́A
�@�P�R�T�O�A�Q�Q�T�O�A�R�P�T�O�A�S�X�T�O�A�T�W�T�O�A�U�V�T�O�A�V�U�T�O�A�W�T�T�O�A�X�S�T�O
���������āA���߂�ꍇ�̐��́A�@�Q�{�X���P�P�i�ʂ�j�@�@�i�I�j
��T���@�@A�w�ł�B�w�s���AC�w�s���AD�w�s���̂R��ނ̓d�Ԃ��A���ꂼ����̊Ԋu��
�@�@���Ԃ���B������A�R��ނ̍ŏ��̓d�Ԃ������ɔ��Ԃ��A�R��ނ̍Ō�̓d�Ԃ�������
�@�@���Ԃ��AB�w�s���́A�P�U�X�{�AC�w�s���́A�V�P�{�AD�w�s���́A�S�P�{���Ԃ����B
�i�P�j�@�R��ނ̓d�Ԃ������ɔ��Ԃ����̂́A�ŏ��ƍŌ���܂߂đS���ʼn��ʂ肠�邩�B
�i�Q�j�@�R��ނ̂����A�Q��ނ̓d�Ԃ݂̂������ɔ��Ԃ����̂͑S���ʼn��ʂ肠�邩�B
�i���j�i�P�j�@B�w�s���AC�w�s���AD�w�s���̂R��ނ̓d�Ԃ̉^�q�Ԋu���́A���ꂼ�����
�Ԋu�Ŕ��Ԃ��邱�Ƃ���A�P�U�W�A�V�O�A�S�O�����ɂȂ�B���̍ŏ����{���́A�W�S�O�@�ł���B
���������āAB�w�s���̓d�Ԃ́A�W�S�O���P�U�W���T�@����A�Ԋu�T���ɏo������B
C�w�s���̓d�Ԃ́A�W�S�O���V�O���P�Q�@����A�Ԋu�P�Q���ɏo������B
D�w�s���̓d�Ԃ́A�W�S�O���S�O���Q�P�@����A�Ԋu�Q�P���ɏo������B
�@�T�A�P�Q�A�Q�P �̍ŏ����{���́A�S�Q�O�@�ł���B
���������āA�R��ނ̓d�Ԃ������ɔ��Ԃ����̂́A�ŏ��ƍŌ���܂߂đS����
�@�W�S�O���S�Q�O�{�P���R�i�{�j
�i�Q�j�@B�w�s���AC�w�s���̓d�Ԃ������ɔ��Ԃ����̂́A�ŏ��ƍŌ���܂߂đS���ŁA
�@�T�A�P�Q�@�̍ŏ����{�����U�O�ł��邩��A�@�W�S�O���U�O�{�P�|�R���P�Q�i�{�j
B�w�s���AD�w�s���̓d�Ԃ������ɔ��Ԃ����̂́A�ŏ��ƍŌ���܂߂đS���ŁA
�@�T�A�Q�P�@�̍ŏ����{�����P�O�T�ł��邩��A�@�W�S�O���P�O�T�{�P�|�R���U�i�{�j
C�w�s���AD�w�s���̓d�Ԃ������ɔ��Ԃ����̂́A�ŏ��ƍŌ���܂߂đS���ŁA
�@�P�Q�A�Q�P�@�̍ŏ����{�����W�S�ł��邩��A�@�W�S�O���W�S�{�P�|�R���W�i�{�j
���������āA�R��ނ̂����A�Q��ނ̓d�Ԃ݂̂������ɔ��Ԃ����̂͑S���ŁA
�@�P�Q�{�U�{�W���Q�U�i�{�j�@�@�i�I�j
��U���@�@���}�́A�P�~�P����X�~�X�̂W�P�̐���\�ɂ������̂ł���B
�@�@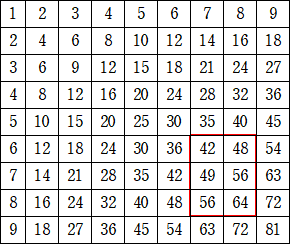
�@�����̒����`�̒��ɏ����ꂽ���ׂĂ̐��̘a�͂R�P�T�ł���B���̕\�̌r���ň͂܂ꂽ
�����`�͑S���łQ�O�Q�T���邪�A���̂����A���ɏ����ꂽ���ׂĂ̐��̘a���R�P�T�ł����
�̂́A�����̒����`���܂߂đS�������邩�B�������A�����`�͒����`�Ɋ܂܂��B
�i���j�@�R�P�T���R2�E�T�E�V�@�Ȃ̂ŁA�����`�̏c�̒��� �� �A���̒��� �� �Ƃ���ƁA�N���蓾���
���́A�i���C���j���i�V�C�S�T�j�A�i�X�C�R�T�j�A�i�P�T�C�Q�P�j�A�i�Q�P�C�P�T�j�A�i�R�T�C�X�j�A�i�S�T�C�V�j�@�̂U�ʂ�
�i���C���j���i�V�C�S�T�j�@�̂Ƃ��A
�@�����V�@�ƂȂ�̂́A�@�V�@�A�R�{�S�@�̂Q�ʂ�ŁA���̂����̂P�ʂ�ɑ��āA
�@�@�����S�T�@�ƂȂ�̂́A�@�P�{�Q�{�R�{�S�{�T�{�U�{�V�{�W�{�X�@�̂P�ʂ�@�Ȃ̂ŁA
�@�Q�~�P���Q�i�j
�i���C���j���i�X�C�R�T�j�@�̂Ƃ��A
�@�����X�@�ƂȂ�̂́A�@�X�@�A�S�{�T�@�A�Q�{�R�{�S�@�̂R�ʂ�ŁA���̂����̂P�ʂ�ɑ��āA
�@�@�����R�T�@�ƂȂ�̂́A�@�T�{�U�{�V�{�W�{�X�A�Q�{�R�{�S�{�T�{�U�{�V�{�W�@�̂Q�ʂ�@�Ȃ̂ŁA
�@�R�~�Q���U�i�j
�i���C���j���i�P�T�C�Q�P�j�@�̂Ƃ��A
�@�����P�T�@�ƂȂ�̂́A�@�V�{�W�@�A�S�{�T�{�U�A�P�{�Q�{�R�{�S�{�T�@�̂R�ʂ�ŁA���̂����̂P��
��ɑ��āA�����Q�P�@�ƂȂ�̂́A�@�U�{�V�{�W�A�P�{�Q�{�R�{�S�{�T�{�U�@�̂Q�ʂ�@�Ȃ̂ŁA
�@�R�~�Q���U�i�j
�i���C���j���i�Q�P�C�P�T�j�@�̂Ƃ��A�i���C���j���i�P�T�C�Q�P�j�@�̂Ƃ��Ɠ��l�ɂ��āA�@�U�i�j
�i���C���j���i�R�T�C�X�j�@�̂Ƃ��A�i���C���j���i�X�C�R�T�j�@�̂Ƃ��Ɠ��l�ɂ��āA�@�U�i�j
�i���C���j���i�S�T�C�V�j�@�̂Ƃ��A�i���C���j���i�V�C�S�T�j�@�̂Ƃ��Ɠ��l�ɂ��āA�@�Q�i�j
�ȏォ��A���߂�ꍇ�̐��́A�@�Q�{�U�{�U�{�U�{�U�{�Q���Q�W�i�j
��V���@�@�W�̐� �R�A�S�A�T�A�U�A�V�A�W�A�X�A�O ����בւ��āAA�AB�AC�AD�AE�AF�AG�AH �ƂȂ����B
�@�@�T���̐��� �PABC�Q ��D�Ċ���Ɗ����A�����S���̐��� EFGH �ɂȂ�Ƃ����B���̂Ƃ��A
�@�@���� EFGH �����߂�B
�i���j�@�N���肤��ꍇ�́A�i�c�C�d�C�g�j���i�R�C�T�C�S�j�A�i�R�C�U�C�S�j�A�i�S�C�R�C�W�j�A�i�U�C�R�C�V�j�@��
�@�@�i����B
�i�c�C�d�C�g�j���i�R�C�T�C�S�j�@�̂Ƃ��A�@�P�`�a�b�Q���T�e�f�S�~�R
�@�g���鐔���́A�U�A�V�A�W�A�X�A�O�@�ŁA�@�T�e�f�S�@�͂R�̔{���Ȃ̂ŁA�N���蓾��ꍇ���
��ƁA
�@�T�U�X�S�~�R���P�V�O�W�Q�@�i�K�j
�@�T�X�U�S�~�R���P�V�W�X�Q�@�i�s�K�j
�@�T�U�O�S�~�R���P�U�W�P�Q�@�i�s�K�j
�@�T�O�U�S�~�R���P�T�P�X�Q�@�i�s�K�j
�@�T�V�W�S�~�R���P�V�R�T�Q�@�i�s�K�j
�@�T�W�V�S�~�R���P�V�U�Q�Q�@�i�s�K�j
�@�T�X�O�S�~�R���P�V�V�P�Q�@�i�s�K�j
�@�T�O�X�S�~�R���P�T�Q�W�Q�@�i�s�K�j
�i�c�C�d�C�g�j���i�R�C�U�C�S�j�@�̂Ƃ��A�@�P�`�a�b�Q���U�e�f�S�~�R
�@�g���鐔���́A�T�A�V�A�W�A�X�A�O�@�ŁA�@�U�e�f�S�@�͂R�̔{���Ȃ̂ŁA�N���蓾��ꍇ���
��ƁA
�@�U�T�X�S�~�R���P�X�V�W�Q�@�i�s�K�j
�@�U�X�T�S�~�R���Q�O�W�U�Q�@�i�s�K�j
�@�U�T�O�S�~�R���P�X�T�P�Q�@�i�s�K�j
�@�U�O�T�S�~�R���P�W�P�U�Q�@�i�s�K�j
�@�U�W�X�S�~�R���Q�O�U�W�Q�@�i�s�K�j
�@�U�X�W�S�~�R���Q�O�X�U�P�@�i�s�K�j
�@�U�W�O�S�~�R���Q�O�S�P�Q�@�i�s�K�j
�@�U�O�W�S�~�R���P�W�Q�T�Q�@�i�s�K�j
�i�c�C�d�C�g�j���i�S�C�R�C�W�j�@�̂Ƃ��A�@�P�`�a�b�Q���R�e�f�W�~�S
�@�g���鐔���́A�T�A�U�A�V�A�X�A�O�@�ŁA�W�~�S���R�Q�@����A�@�f�~�S�{�R�@�̈�̈ʂ��b�ƂȂ�
�ꍇ�́A�i�b�C�f�j���i�V�C�U�j�@�݂̂ŁA�`�A�a�A�e �Ɏg���鐔���́A�T�A�X�A�O
�@�R�T�U�W�~�S���P�S�Q�V�Q�@�i�s�K�j
�@�R�X�U�W�~�S���P�T�W�V�Q�@�i�s�K�j
�@�R�O�U�W�~�S���P�Q�Q�V�Q�@�i�s�K�j
�i�c�C�d�C�g�j���i�U�C�R�C�V�j�@�̂Ƃ��A�@�P�`�a�b�Q���R�e�f�V�~�U
�@�g���鐔���́A�S�A�T�A�W�A�X�A�O�@�ŁA�@�R�e�f�V�@�͂R�̔{���Ȃ̂ŁA�N���蓾��ꍇ���
��ƁA
�@�R�T�X�V�~�U���Q�P�T�W�Q�@�i�s�K�j
�@�R�X�T�V�~�U���Q�R�V�S�Q�@�i�s�K�j
�@�R�W�X�V�~�U���Q�R�R�W�Q�@�i�s�K�j
�@�R�X�W�V�~�U���Q�R�X�Q�Q�@�i�s�K�j
�@�R�T�O�V�~�U���Q�P�O�S�Q�@�i�s�K�j
�@�R�O�T�V�~�U���P�W�R�S�Q�@�i�s�K�j
�@�R�O�W�V�~�U���P�W�T�Q�Q�@�i�s�K�j
�@�R�W�O�V�~�U���Q�Q�W�S�Q�@�i�s�K�j
�@�ȏォ��A���߂鐔�́A�@�T�U�X�S�@�@�i�I�j
�i�R�����g�j�@�n���ɏꍇ��s�����ċ��߂܂������A�����Ə�肢��@�͂Ȃ���ł����ˁH
��W���@�@���}�̂悤�ɁA���s�l�ӌ`ABCD������A�_E�AF�͕�BC���R�������A�_G�AH�AI ��
�@�@��AD���S�������Ă���B�R����BD�AEl�AFG�ň͂܂ꂽ���o�p�q�̖ʐς͕��s�l�ӌ`ABCD
�@�@�̖ʐς̉��{���B
�@�@
�i���j�@���s�l�ӌ`ABCD�̖ʐς��r�Ƃ����ƁA
�@���a�d�o���i�P/�Q�j�r�~�i�P/�R�j�~�i�S/�V�j���i�Q/�Q�P�j�r�@�A���a�e�o���Q���a�d�o���i�S/�Q�P�j�r
�܂��A�@���a�e�p���i�W/�P�V�j���a�e�f���i�W/�P�V�j�~�i�Q/�R�j�~�i�P/�Q�j�r���i�W/�T�P�j�r�@�Ȃ̂ŁA
���o�e�p�����a�e�o�|���a�e�p���i�S/�Q�P�j�r�|�i�W/�T�P�j�r���i�S/�P�P�X�j�r
����āA�@���o�f�p���i�X/�W�j���o�e�p���i�X/�Q�R�W�j�r�@���A
�@���o�e�f���i�S/�P�P�X�j�r�{�i�X/�Q�R�W�j�r���i�P/�P�S�j�r�@�Ȃ̂ŁA
�@���o�e�q���i�P/�P�S�j�r�~�i�Q/�T�j���i�P/�R�T�j�r
�ȏォ��A���o�p�q���i�S/�P�P�X�j�r�|�i�P/�R�T�j�r���i�R/�T�X�T�j�r�@�ƂȂ�B�@�@�i�I�j
��X���@�@���}�̂悤�ɁAAF�a�Ƃ��锼�~�̎�(��������)��_B�AC�AD�AE ���T��������
�@�@����B�܂��A����AD�ƒ���BE�͓_G�Ō�����Ă���B�Z�p�`ABCDEF�̖ʐς��U�O����2
�@�@�̂Ƃ��A���F�����̌܊p�`CDEFG�̖ʐς����߂�B
�@�@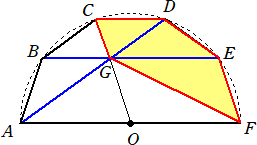
�i���j�@�l�p�`�n�e�d�f�͕��s�l�ӌ`�Ȃ̂ŁA�@���n�e�f�����d�f�e�����d�n�e
�@�Z�p�`ABCDEF�̖ʐς��U�O����2�Ȃ̂ŁA���d�n�e���P�Q����2 ���A�@���n�e�f���P�Q����2
�@����āA���߂�ʐς́A�@�P�Q�~�R�|�P�Q���Q�S�i����2�j�@�@�i�I�j
�i�R�����g�j�@���߂�ʐς́A�l�p�`�n�b�c�d�̖ʐςɓ������̂ŁA�@�P�Q�~�Q���Q�S�i����2�j�@��
�@�@�@�@��������������������Ȃ��B
��P�O���@�@�Œ肳�ꂽ�P�ӂ̒������U�����̐����`(�ΐF����)������A���}�̂悤�ɂP�ӂ�
�@�@�������U�����̐����`ABCD���@�̈ʒu�ɒu����Ă���B
�@�@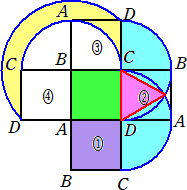
�@�����`ABCD�_D�̎���ɂP�W�O����]�����A�A�̈ʒu�Ɉړ�������B����ɁA�����`
ABCD��1�̒��_�̎���ɂP�W�O����]�����A�A�̈ʒu����B�̈ʒu�ɁA�B�̈ʒu����C
�̈ʒu�Ɉړ�������B
�@���̈ړ��ɂ����āA��CD���ʉ߂��镔���̖ʐς́A�P�ӂ̒������U�����̐��O�p�`�̖�
�ς�肢���傫���Ȃ邩�B
�i���j�@���F�����̖ʐς́A�@�R�U�~�i�Q/�R�j���Q�S�i����2�j
���F�����̖ʐς́A�}�`�`�c�b�̔������b�c�`�ɕt���ւ��āA
�@�i�U �j2�~�i�P/�Q�j�|�R�U�~�i�P/�Q�j���P�W�i����2�j
�j2�~�i�P/�Q�j�|�R�U�~�i�P/�Q�j���P�W�i����2�j
����āA���߂�ʐς́A�@�S�Q�i����2�j�@�@�i�I�j
��P�P���@�@���}�̑����ŕ\���ꂽ���̂́A�܊p�`���ʂƂ���܊p�����P�̕��ʂłQ��
�@�@�ɕ����������̂P�Ă���B���̗��̂̑̐ς����߂�B�������A�����̒P�ʂ́A�����Ƃ���B
�@�@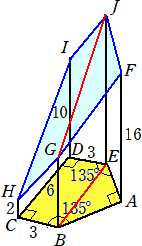
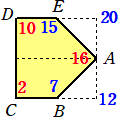
�i���j�@��ʂ̌܊p�`�̊e���_�ɂ����闧�̂̍��������߂�ƁA
�@�@
���������āA���߂闧�̂̑̐ς́A
�@�P�W�~�i�Q�{�V�{�P�T�{�P�O�j/�S�{�X�~�i�V�{�P�U�{�P�T�j/�R���P�T�R�{�P�P�S���Q�U�V�i����3�j�@�@�i�I�j
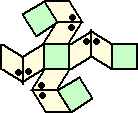
��P�Q���@�Q�̗���A�A�a������B�����}�͗���A�̓W�J�}�A�E���}�͗���B�̓W�J�}�ł�
�@�@��B����A�AB�̕ӂ̒����͂��ׂ�1Ocm�ł���B�܂��A���F�����̎l�p�`�͂��ׂĐ����`
�@�@�ŁA���ۂ������p�̑傫���͂��ׂĂU�O���ł���B���̂Ƃ��A����A�̑̐ς͗���B�̑�
�@�@�ς̉��{���B
| �@ |
 |
|
 |
�i���j�@�����}�̐}�`�̔����i���F�����ƗΐF�����j
�@�@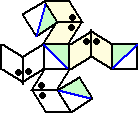
�ŗ��̐}�`��g�ݗ��Ă�ƁA���}�̂悤�ɂȂ�B
�@�@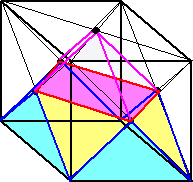
�@�P�ӂ̒������P�O �̗����̂ŁA�s���N�F�̎l�p�`�́A�P�ӂ̒������P�O�̐����`�ƂȂ�B
�̗����̂ŁA�s���N�F�̎l�p�`�́A�P�ӂ̒������P�O�̐����`�ƂȂ�B
���ϕό`���s�����Ƃɂ��A��L���̂̑̐ς́A�@�P�O �~�P�O
�~�P�O �~�T
�~�T ���P�O�O�O
���P�O�O�O
�Ȃ̂ŁA�����}�̐}�`�ō���闧��A�̑̐ς́A�@�Q�O�O�O �@�ƂȂ�B
�@�ƂȂ�B
�@����A�E���}�̗���B�̑̐ς́A�@�P�O�~�P�O�~�T �~�i�P/�R�j���i�T�O�O/�R�j
�~�i�P/�R�j���i�T�O�O/�R�j
����āA�Q�O�O�O ���i�T�O�O/�R�j
���i�T�O�O/�R�j ���P�Q�@���A
���P�Q�@���A
�@����A�̑̐ς͗���B�̑̐ς̂P�Q�{�ƂȂ�B�@�@�i�I�j
�i�Q���ځj
��P���@�@�R�R�U�U�����ꂽA����B���̊Ԃɒn�_C�A�n�_D������B�Ԏq�͉����̉ו���
�@�@������A�����o����B���ցA���Y�͉ו�����������B�����o����A���������Đi�ށB
�@�Q�l�������ɏo�������Ƃ���A�Q�l�͒n�_C�ŏo������B�����ŁA�Ԏq�͎����Ă����ו���
���傤�ǔ����̌��Y�ɓn�����B���Y���Ԏq���A�����Ă���ו����P���邲�Ƃɐi��
�����͕����P�������Ȃ�A�P�����邲�Ƃɐi�ޑ����͕����P���x���Ȃ�B
�@�n�_C�ʼnו����n�������ƁA�Ԏq�Ƒ��Y�͂��ꂼ��B���������Đi�B��ɑ��Y
�� B���ɓ������A�ו������ׂĒu���āA�ŏ��̑�����A���������Đi�B���̌�A�Q�l
�͒n�_D�ōĂяo������B
�@�Ԏq�͎c��̉ו������ׂđ��Y�ɓn���āAA���ֈ����Ԃ��AA���ɓ���������͂����ɗ�
�܂����B���Y��B���������Đi�݁AB���ɓ���������͂����ɗ��܂����B
�@���̃O���t�́A�Q�l�������ɏo�����Ă���̎��ԂƂQ�l�̊Ԃ̋����̊W��\�������̂�
����B�Ȃ��A�ו���u�����Ԃ�n���̎��Ԃ͍l���Ȃ����̂Ƃ��A�����Ă���ו�������
���̂Ƃ��͐i�ޑ��������Ƃ���B
�i�P�j�@�͂��߁A�Ԏq�͉��̉ו���������A�����o���������B�܂��A���Y�́A����������B��
�@���o���������B
�i�Q�j�@�s1�A�s2 �͏o�����Ă��牽���ォ�B
�@�@
�i���j�i�P�j�@��ӂ��A�Ԏq�Ƒ��Y�̍s�������ꂼ��܂Ƃ߂ĉ��}��B
�@�@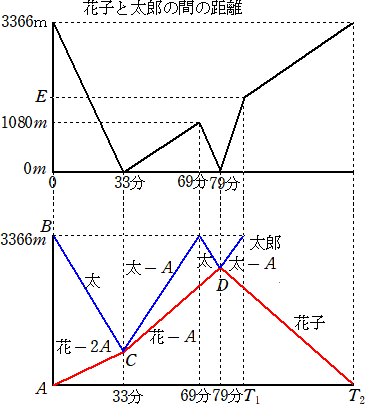
�@�Ԏq�A���Y�̕��������ꂼ��u�ԁv�A�u���v�ŕ\���B�܂��A�Ԏq���Q�`�̉ו���������A��
���o�������Ƃ���B��ӂ��A
�@�i�i�ԁ|�QA�j�{���j�~�R�R���R�R�U�U�@���A�@�i�ԁ|�QA�j�{�����P�O�Q
�܂��A�@�i�i�ԁ|�`�j�{���j�~�P�O���P�O�W�O�@���A�@�i�ԁ|A�j�{�����P�O�W�@�Ȃ̂ŁA�@�`���U
���������āA�͂��߁A�Ԏq�͂P�Q�̉ו���������A�����o�������B
�@���̂Ƃ��A�@�ԁ{�����P�P�S�@�ł���B
�܂��A�@�i���|�`�j�~�R�U�|�i�ԁ|�`�j�~�R�U���P�O�W�O�@����A�@���|�ԁ��R�O�@�Ȃ̂ŁA
�@�Q�����P�S�S�@����A�@�����V�Q�@���Ȃ킿�A���Y�̕����́A�V�Q��/���@�ł���B
���̂Ƃ��A�Ԏq�̕����́A�@�S�Q��/���@�ƂȂ�B
�i�Q�j�@�a�c�Ԃ̋����́A�P�O�W�O�|�i�S�Q�|�U�j�~�P�O���V�Q�O�i���j�@�Ȃ̂ŁA
�@�s1���V�X�{�V�Q�O���i�V�Q�|�U�j���V�X�{�P�Q�O/�P�P���X�W�X/�P�P�i���j
�@�`�c�Ԃ̋����́A�R�R�U�U�|�V�Q�O���Q�U�S�U�i���j�@�Ȃ̂ŁA
�@�s2���V�X�{�Q�U�S�U/�S�Q���P�S�Q�i���j�@�@�i�I�j
��Q���@�@���ɂ������̐�����������Ă���Ƃ��A���̂悤�ȂQ�̐�������Ō��Ԃ���
�@�@�ɂ���B
�@�u����̐����̂����ꂩ�P�̈ʂ̐����������Ƒ����̐����ɂȂ�v
�������A�ł��傫���ʂ̐������O�ɂȂ�悤�ȏ������͂��Ȃ����̂Ƃ���B�܂��A�R���̐���
�̏\�̈ʂ������Ƃ��́A���Ƃ̐����̕S�̈ʂƁ[�̈ʂ��Ȃ��ĂQ���̐����ƍl����B
�@���Ƃ��ρA���� �R�A�S�A�Q�S�A�R�S�A�Q�O�S�A�Q�R�S ��������Ă���Ƃ��A
�@�R�ƂR�S�A�S�ƂQ�S�A�S�ƂR�S�A�Q�S�ƂQ�O�S�A�Q�S�ƂQ�R�S�A�R�S�ƂQ�R�S����Ō��Ԃ̂ŁA���̖{����
�U�{�ł���B
�i�P�j�@���ɂP�O����X�X�܂ł̂X�O�̐����ƂP�Q�R�ƂS�T�T�́A���킹�ĂX�Q�̐���������
�@�@��Ă���Ƃ��A���̖{���͑S���ʼn��{���B
�i�Q�j�@���ɂP����X�X�܂ł̂X�X�̐�����������Ă���Ƃ��A���̖{���͑S���ʼn��{���B
�i�R�j�@���ɂP�O����X�X�X�܂ł̂X�X�O�̐�����������Ă���Ƃ��A���̖{���͑S���ʼn�
�@�@�{���B
�i���j�i�P�j�@�P�Q�R���P�Q�A�P�R�A�Q�R�@�A�S�T�T���S�T�A�T�T�@���A���̖{���́A�T�{
�i�Q�j�@�P�O���P�@�A�P�P���P�@�A�P�Q���P�A�Q�@�A�P�R���P�A�R�@�A�P�S���P�A�T�@�A�P�T���P�A�T
�@�P�U���P�A�U�@�A�P�V���P�A�V�@�A�P�W���P�A�W�@�A�P�X���P�A�X�@�̂P�W�{
���l�ɂ��āA�Q�O�`�Q�X�@�̐��̖{���́A�P�W�{
�R�O�`�R�X�@�̐��̖{���́A�P�W�{
�S�O�`�S�X�@�̐��̖{���́A�P�W�{
�T�O�`�T�X�@�̐��̖{���́A�P�W�{
�U�O�`�U�X�@�̐��̖{���́A�P�W�{
�V�O�`�V�X�@�̐��̖{���́A�P�W�{
�W�O�`�W�X�@�̐��̖{���́A�P�W�{
�X�O�`�X�X�@�̐��̖{���́A�P�W�{
�@���������āA���߂���̖{���́A�@�P�W�~�X���P�U�Q�i�{�j
�i�R�j�@�i�Q�j�Ɠ��l�ɍl���āA
�P�O�O�`�P�O�X�@�̐��̖{���́A�@�P�X�{
�P�P�O�`�P�P�X�@�̐��̖{���́A�@�P�X�{
�P�Q�O�`�P�Q�X�@�̐��̖{���́A�@�Q�{�R�~�X���Q�X�i�{�j
�P�R�O�`�P�R�X�@�̐��̖{���́A�@�Q�{�R�~�X���Q�X�i�{�j
�P�S�O�`�P�S�X�@�̐��̖{���́A�@�Q�{�R�~�X���Q�X�i�{�j
�P�T�O�`�P�T�X�@�̐��̖{���́A�@�Q�{�R�~�X���Q�X�i�{�j
�P�U�O�`�P�U�X�@�̐��̖{���́A�@�Q�{�R�~�X���Q�X�i�{�j
�P�V�O�`�P�V�X�@�̐��̖{���́A�@�Q�{�R�~�X���Q�X�i�{�j
�P�W�O�`�P�W�X�@�̐��̖{���́A�@�Q�{�R�~�X���Q�X�i�{�j
�P�X�O�`�P�X�X�@�̐��̖{���́A�@�Q�{�R�~�X���Q�X�i�{�j
�@����āA�@�P�O�O�`�P�X�X�@�̐��̖{���́A�@�P�X�~�Q�{�Q�X�~�W���Q�V�O�i�{�j
���l�ɂ��āA
�Q�O�O�`�Q�X�X�@�̐��̖{���́A�@�P�X�~�Q�{�Q�X�~�W���Q�V�O�i�{�j
�R�O�O�`�R�X�X�@�̐��̖{���́A�@�P�X�~�Q�{�Q�X�~�W���Q�V�O�i�{�j
�S�O�O�`�S�X�X�@�̐��̖{���́A�@�P�X�~�Q�{�Q�X�~�W���Q�V�O�i�{�j
�T�O�O�`�T�X�X�@�̐��̖{���́A�@�P�X�~�Q�{�Q�X�~�W���Q�V�O�i�{�j
�U�O�O�`�U�X�X�@�̐��̖{���́A�@�P�X�~�Q�{�Q�X�~�W���Q�V�O�i�{�j
�V�O�O�`�V�X�X�@�̐��̖{���́A�@�P�X�~�Q�{�Q�X�~�W���Q�V�O�i�{�j
�W�O�O�`�W�X�X�@�̐��̖{���́A�@�P�X�~�Q�{�Q�X�~�W���Q�V�O�i�{�j
�X�O�O�`�X�X�X�@�̐��̖{���́A�@�P�X�~�Q�{�Q�X�~�W���Q�V�O�i�{�j
�@���������āA���߂���̖{���́A�@�Q�V�O�~�X���Q�S�R�O�i�{�j�@�@�i�I�j
��R���@�@�i�P�j�@���}�̎l�p�`ABCD�́A�P�ӂ̒������R�����̐����`�ŁAAE�ABF�ACG�ADH
�@�@�̒����͂��ׂĂP�����ł���B���̂Ƃ��A���F�����̖ʐς����߂�B
�@�@
�i�Q�j�@�����}�́A�P�������̂܂��ڂ�p���ĂR�̕��s�l�ӌ`�����������̂ł���B���̐}�`
�@��_P�̂܂탊�Ɏ��v���ɂX�O����]�����āA���Ƃ̐}�`�Əd�˂�ƁA�E���}�̂悤�ɂȂ�B
�@���Ƃ̂R�̕��s�l�ӌ`�Ɖ�]�������R�̕��s�l�ӌ`���d�Ȃ镔���S��(�E���}�̗ΐF
�@����)�̖ʐς����߂�B
| �@ |
 |
�@ |
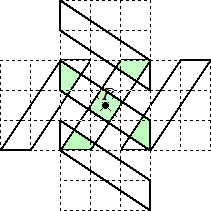 |
�i�R�j�@�i�Q�j�̍����}�̐}�`��_Q�̂܂��Ɏ��v���ɂX�O����]�����āA���Ƃ̐}�`�Əd
�@�˂��Ƃ��A���Ƃ̂R�̕��s�l�ӌ`�Ɖ�]�������R�̕��s�l�ӌ`���d�Ȃ镔���S��(�E
�@���}�̗ΐF����)�̖ʐς����߂�B
| �@ |
 |
�@ |
 |
�i���j�i�P�j�@���a�p�d�䁢�a�o�`�@�ŁA�����䂪 �Q �F �R ���A���a�p�d �F ���a�o�`���S �F �X�@���A
�@���a�p�d���S�r�@�Ƃ����ƁA�@�l�p�`�d�p�o�`���T�r�@�ƂȂ�B���l�ɁA
���`�o�g�����c�r�f�����b�q�e���S�r�@�A�l�p�`�g�o�r�c���l�p�`�f�r�q�f���l�p�`�e�q�p�a���T�r
�@�l�p�`�o�p�q�r�͐����`�ł���B
�@���d�a�b���P�R�r���R�@���A�@�r���R/�P�R
����āA�@�����`�`�a�b�c���R�U�r�{�l�p�`�o�p�q�r���X�@���A�@
�@�l�p�`�o�p�q�r���X�|�P�O�W/�P�R���X/�P�R
���������āA���߂�ʐς́A�@�Q�O�r�{�l�p�`�o�p�q�r���U�O/�P�R�{�X/�P�R���U�X/�P�R�i����2�j
�i�Q�j�@�i�P�j�̌��ʂ���A�l�p�`�o�p�q�r���S�����������悢�̂ŁA
�@�U�X/�P�R�|�i�X/�P�R�j�~�S���R�R/�P�R�i����2�j
�i�R�j�@�i�Q�j�̌��ʂ��A�o�̂܂��̂S�̑�`�̖ʐς́A�R�R/�P�R�|�X/�P�R���Q�S/�P�R�@�Ȃ̂ŁA
���̂����̈�̑�`�̖ʐς́A�@�i�Q�S/�P�R�j���S���U/�P�R�@�ƂȂ�B
����āA����̂Q�̎O�p�`�̖ʐς̘a�́A�@�P�~�i�R/�Q�j�~�i�P/�Q�j�|�U/�P�R���P�T/�T�Q
���������āA���߂�ʐς́A�@�i�P�T/�T�Q�j�~�Q�{�i�X/�P�R�j�~�Q���T�P/�Q�U�i����2�j�@�@�i�I�j
��S���@�@���}�̂悤�ɁA�P�ӂ̒������U�����̗�����ABCD-EFGH ������B�_ I�AJ�AK �͂�
�@�@�ꂼ���CD�AAE�AFG��ɂ���ADI�AAJ�AGK�̒����͂��ꂼ��P�����A�Q�����A�Q�����ł���B
�@�@�R�_ I�AJ�AK��ʂ镽�ʂŁA���̗����̂��B
�@�@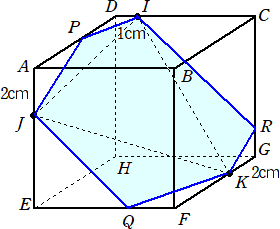
�i�P�j�@�蕪�����Q�̗��̂̂����A�_H���܂ޕ��̗��̂̑̐ς����߂�B
�i�Q�j�@����̖ʐς͎O�p�`IJK�̖ʐς̉��{���B
�i���j�i�P�j�@������ ��Ԃōl����B
�@�@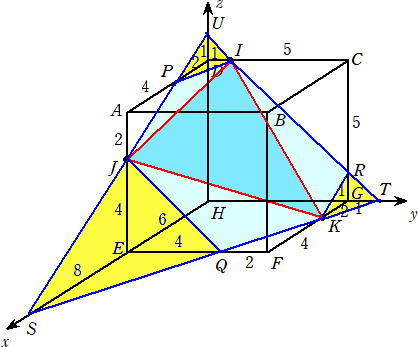
�@�R�_ �h�i�O�C�P�C�U�j�A�i�i�U�C�O�C�S�j�A�j�i�Q�C�U�C�O�j��ʂ镽�ʂ̕��������@�����{�����{���������@��
�����ƁA
�@���{�U�������@�A�U���{�S�������@�A�Q���{�U�������@�Ȃ̂ŁA�����Q���@�A�����Q���@�A�����P�S��
�����O�@�Ȃ̂ŁA���� �h�i�j�̕������́A�@���{�Q���{�Q�����P�S
����āA�t�i�O�C�O�C�V�j�A�r�i�P�S�C�O�C�O�j�A�s�i�O�C�V�C�O�j�@�ƂȂ�B
�܂��A�����r�s�̕����� ���{�Q�����P�S�@���A�p�i�U�C�S�C�O�j
�����s�t�̕����� ���{�����V�@���A�q�i�O�C�U�C�P�j
�����t�r�̕����� ���{�Q�����P�S�@���A�o�i�Q�C�O�C�U�j
���������āA�O�p���t-�r�s�g�̑̐ς́A�@�P�S�E�V�E�i�P/�Q�j�E�V�E�i�P/�R�j���R�S�R/�R
�܂��A�O�p���t-�o�h�c�̑̐ς́A�Q�E�P�E�i�P/�Q�j�E�P�E�i�P/�R�j���P/�R
�O�p���i-�r�p�d�̑̐ς́A�W�E�S�E�i�P/�Q�j�E�S�E�i�P/�R�j���U�S/�R
�O�p���q-�j�s�f�̑̐ς́A�Q�E�P�E�i�P/�Q�j�E�P�E�i�P/�R�j���P/�R
�ȏォ��A���߂闧�̂̑̐ς́A�@�R�S�R/�R�|�P/�R�|�U�S/�R�|�P/�R���Q�V�V/�X
�i�Q�j�@�h�i���i�U�C�|�P�C�|�Q�j�@�A�h�j���i�Q�C�T�C�|�U�j�@���A
�@�h�i2���S�P�A�h�j2���U�T�A�h�i�E�h�j���P�X�@�Ȃ̂ŁA���h�i�j���i�P/�Q�j��i�S�P�E�U�T�|�P�X2�j���Q�S
�g�i�O�C�O�C�O�j�ƕ��� ���{�Q���{�Q�����P�S �̋����́A�@�P�S/�R
�O�p���t-�r�s�g�̑̐ς́A�R�S�R/�R�@�Ȃ̂ŁA�@���r�s�t�E�i�P�S/�R�j�E�i�P/�R�j���R�S�R/�R�@���A
�@���r�s�t���P�S�V/�Q�@�ƂȂ�B
�܂��A���r�p�i�䁢�r�s�t�@�Ȃ̂ŁA���r�p�i �F ���r�s�t���S2 �F �V2���P�U �F �S�X�@���A
�@���r�p�i���i�P�U/�S�X�j���r�s�t���Q�S�@�ƂȂ�B
���l�ɁA�@���r�p�i�䁢�o�h�t�@�Ȃ̂ŁA���r�p�i �F ���o�h�t���S2 �F �P2���P�U �F �P�@���A
�@���o�h�t���i�P/�P�U�j���r�p�i���R/�Q�@���l�ɁA�@���j�s�q���R/�Q
���������āA����̖ʐς́A�@�P�S�V/�Q�|�Q�S�|�R/�Q�|�R/�Q���X�R/�Q
����āA�X�R/�Q���Q�S���R�P/�P�U ���A����̖ʐς͎O�p�` IJK�̖ʐς̂R�P/�P�U�{�@�@�i�I�j
�i�R�����g�j�@��ԍ��W�̋Z��p���ĉ������̂����A������Ə��w�����ۂ��Ȃ������H�ł��A
�@�@�@�@�咆�w�̎��̒��ɂ́A��L�̂悤�ɉ������l�������Ƃ��邾�낤�B
��T���@�@���̖��ł́A�Z�ɂ� �O�A�P�A�Q�A�R�A�S�A�T�A�U�A�V�A�W�A�X �̂����ꂩ�̐�������B
�@�@���}�̂悤�ɁA��̒i�̂��Ƃ��ɐ��������Ă���Ƃ��A���́i�K���j�ɂ��������ĉ��̒i��
�@�@���ɐ������邱�Ƃ��m����n�ƌĂӂ��Ƃɂ���B
�@�@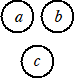
�i�K���j�@�E ���{�� �̒l���X�ȉ��̂Ƃ��́A���̒l�����Ƃ���B
�@�@�E ���{�� �̒l���P�O�ȏ�̂Ƃ��́A���̒l�́[�̈ʂ̐��Ə\�̈ʂ̐��̘a�����Ƃ���B
�@��ԏ�̒i�̊e�Z�̒��ɂO����X�܂ł̂����ꂩ�̐������A[����]���J��Ԃ����ƂŁA
�����艺�̒i�́Z�̒��ɐ������Ă����B
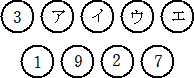
�i�P�j�@���}�̏�Ԃ���m����n���J��Ԃ����Ƃ��A���̒i�̂S�́Z�̒��ɂ͍����珇��
�@�P�A�X�A�Q�A�V������B���̂悤�ȃA�A�C�A�E�A�G�̐��̑g�͂Q����B���̂����̂P����B
�@�@
�i�Q�j�@���}�̏�Ԃ���m����n���J��Ԃ����Ƃ��A��ԉ��̒i�̂S�́Z�̒��ɂ͍����珇��
�@�Q�A�O�A�Q�A�T������B���̂悤�ȃI�A�́A�L�A�N�A�P�A�R�̐��̑g��1�����ł���B���̑g��
�@������B
�@�@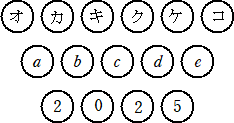
�i�R�j�@���}�̏�Ԃ���m����p���J��Ԃ��B�O����X�܂ł̐�����Ȃ�S�̐�A�AB�AC�AD�̑g
�@�͑S���� �P�O�O�O�O���邪�A���̂����A�T�A�V�A�X�A�Z�A�\�ɐ����ǂ̂悤�ɓ���Ă������
�@�Ȃ����̂̌������߂�B
�@�@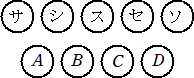
�i���j�i�P�j�@�R�{�A���P�@���A�@�A���V�@�Ɗm�肷��B�V�{�C���X�@���A�@�C���Q�@�Ɗm�肷��B
�@�Q�{�E���Q�@����A�E���O�@�܂��́@�X�@�Ɗm�肷��B
�@�E���O�@�̂Ƃ��A�@�O�{�G���V�@����A�G���V�@�Ɗm�肷��B
�@�E���X�@�̂Ƃ��A�@�X�{�G���V�@����A�G���V�@�Ɗm�肷��B
�ȏォ��A�@�i�A�C�C�C�E�C�G�j���i�V�C�Q�C�O�C�V�j�A�i�V�C�Q�C�X�C�V�j
�i�Q�j�@�m����n�ŁA�O�ɂȂ�Q�̐��́A�O�A�O�@�����Ȃ��̂ŁA���������O�A�J���L���N���O
�@�����O�@����A�����Q�@�ŁA�J���O�@����A�I���Q
�@�����O�@����A�����Q�A�P���Q�@�Ɗm�肷��B
���̂Ƃ��A�����R�@�ŁA�R���P�@�Ɗm�肷��B
�ȏォ��A�@�i�I�C�J�C�L�C�N�C�P�C�R�j���i�Q�C�O�C�O�C�O�C�Q�C�P�j
�i�R�j�@�`�a�b�c���O�@�̂Ƃ��́A�i�T�C�V�C�X�C�Z�C�\�j�͑��݂���B
�@�`�A�a�A�b�A�c�@�����ׂĂO�̂Ƃ��A�i�T�C�V�C�X�C�Z�C�\�j���i�O�C�O�C�O�C�O�C�O�j�ł���悢�B
�@�`�A�a�A�b�A�c�@�̂����A�R���O�̂Ƃ��A�`�a�b�A�`�a�c�A�`�b�c�A�a�b�c�ŏꍇ��������B
�@�`�a�b���S���O�̂Ƃ��A�i�T�C�V�C�X�C�Z�C�\�j���i�O�C�O�C�O�C�O�C�c�j�ł���悢�B
�@�`�a�c���S���O�̂Ƃ��A�i�T�C�V�C�X�C�Z�C�\�j���i�O�C�O�C�O�C�O�C�O�j�Ȃ̂ŁA�c���O�ƂȂ�B
�@���������āA�c���P�A�Q�A�E�E�E�A�X�@�Ȃ�A���̂悤�ȑg�����͋N���蓾�Ȃ��B���@�X�ʂ�
�@�`�b�c���S���O�̂Ƃ��A�i�T�C�V�C�X�C�Z�C�\�j���i�O�C�O�C�O�C�O�C�O�j�Ȃ̂ŁA�a���O�ƂȂ�B
�@���������āA�a���P�A�Q�A�E�E�E�A�X�@�Ȃ�A���̂悤�ȑg�����͋N���蓾�Ȃ��B���@�X�ʂ�
�@�a�b�c���S���O�̂Ƃ��A�i�T�C�V�C�X�C�Z�C�\�j���i�`�C�O�C�O�C�O�C�O�j�ł���悢�B
�@�`�A�a�A�b�A�c�@�̂����A�Q���O�̂Ƃ��A�`�a�A�`�b�A�`�c�A�a�b�A�a�c�A�b�c�ŏꍇ��������B
�@�`�a���S���O�̂Ƃ��A�i�T�C�V�C�X�C�Z�C�\�j���i�O�C�O�C�O�C�b�C*�j�ł���悢�B
�@�`�b���S���O�̂Ƃ��A�i�T�C�V�C�X�C�Z�C�\�j���i�O�C�O�C�O�C�O�C�c�j�ŁA�a���O�A�c���O�@�ƂȂ�B
�@���������āA�a���P�A�Q�A�E�E�E�A�X�@�ŁA�c���O�@�Ȃ�A�N���蓾�Ȃ��B���@�X�~�X���W�P�i�ʂ�j
�@�`�c���S���O�̂Ƃ��A�i�T�C�V�C�X�C�Z�C�\�j���i�O�C�O�C�a�i�b�j�C�O�C�O�j�ŁA�a�i�b�j���O�@�ƂȂ�B
�@���������āA�a�i�b�j���P�A�Q�A�E�E�E�A�X�@�ŁA�a�A�b���قȂ�ꍇ�͋N���蓾�Ȃ��B���@�X�~�W���V�Q�i�ʂ�j
�@�a�b���S���O�̂Ƃ��A�i�T�C�V�C�X�C�Z�C�\�j���i�`�C�O�C�O�C�O�C�c�j�ł���悢�B
�@�a�c���S���O�̂Ƃ��A�i�T�C�V�C�X�C�Z�C�\�j���i�`�C�O�C�O�C�O�C�O�j�ŁA�b���O�A�`���O�@�ƂȂ�B
�@���������āA�b���P�A�Q�A�E�E�E�A�X�@�ŁA�`���O�@�Ȃ�A�N���蓾�Ȃ��B���@�X�~�X���W�P�i�ʂ�j
�@�b�c���S���O�̂Ƃ��A�i�T�C�V�C�X�C�Z�C�\�j���i*�C�a�C�O�C�O�C�O�j�ł���悢�B
�ȏォ��A���߂�ꍇ�̐��́A�@�X�{�X�{�W�P�{�V�Q�{�W�P���Q�T�Q�i�j�@�@�i�I�j
�@�咆�w�������́A�\���y���߂܂����ˁI�咆�w�ȊO�̒��w��������T�K���Ă���
�܂��傤�B
���M�i�Q�O�Q�T�j
��R���@�@�� �����R���Ƃ��A����������3�@�ƒ�߂�B���̂Ƃ��A���̖₢�ɓ�����B
�i�P�j�@�� ���P�ȏ�P�Q�ȉ��̂Ƃ��A�������̒l�Ɓ��������X�Ŋ������]������߂�B
�i�Q�j�@�������{�������{���������P�P�P�P�@�ł��邱�Ƃ������B
�i�R�j�@�������{�������{�������{���������Q�O�Q�T�@�ƂȂ� ���A���A���A�� (�������A�������������� )
�@�����߂�B
�i���j�i�P�j�@���̕\��B
| �� |
�P |
�Q |
�R |
�S |
�T |
�U |
�V |
�W |
�X |
�P�O |
�P�P |
�P�Q |
| ������ |
�P |
�W |
�Q�V |
�U�S |
�P�Q�T |
�Q�P�U |
�R�S�R |
�T�P�Q |
�V�Q�X |
�P�O�O�O |
�P�R�R�P |
�P�V�Q�W |
| �]�� |
�P |
�W |
�O |
�P |
�W |
�O |
�P |
�W |
�O |
�P |
�W |
�O |
�i�Q�j�@�i�P�j���A���������X�Ŋ������]��́A�O�A�P�A�W �̉��ꂩ�ł���B
�@���������āA�������{�������{���������X�Ŋ������]��́A�O�A�P�A�Q�A�R�A�U�A�V�A�W
�����ŁA�P�P�P�P�߂S�@�i�������@�X�j�@�Ȃ̂ŁA�������{�������{���������P�P�P�P�@�ł���B
�i�R�j�@�Q�O�Q�T�́A�X�̔{���ł���B�P�A�W�A�O�̂�������d���������ĂS�I�ԂƂ��A�X�Ŋ�����
�]�肪�O�ƂȂ�̂́A�@�O�O�O�O�@�܂��́@�P�P�W�W�@�ł���B
�@�O�O�O�O�@�̏ꍇ�A�@�Q�V�A�Q�P�U�A�V�Q�X�A�P�V�Q�W�@��g�ݍ��킹�Ă��A
�@�������{�������{�������{���������Q�O�Q�T�@�ƂȂ邱�Ƃ͂Ȃ��B
�@�P�P�W�W�@�̏ꍇ�A�@�]�肪�P�ƂȂ�̂́A�@�P�A�U�S�A�R�S�R�A�P�O�O�O
�@�@�]�肪�W�ƂȂ�̂́A�@�W�A�P�Q�T�A�T�P�Q�A�P�R�R�P
�Ȃ̂ŁA�g�ݍ��킹�āA�@�P�{�T�P�Q�{�T�P�Q�{�P�O�O�O�@�܂��́A�@�W�{�R�S�R�{�R�S�R�{�P�R�R�P
���������āA���߂� ���A���A���A�� �̒l�́A�@�P�C�W�C�W�C�P�O�@�܂��́@�Q�A�V�A�V�A�P�P�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�Q���S���i�j�t�������V�������ɗߘa�V�N�x�������w������肪�f��
�@�@�@���ꂽ�B���������肪�������̂Œ��킵�Ă݂��B�i�ꕔ����j
�h�i�R�j�@���鐮�������S�Ŋ������]����������A�V�Ŋ������]���[��]�ŕ\���B���̖₢�ɓ�����B
�i�C�j�@���������R�ł���P�ȏ�̐����������������ɕ��ׂ��Ƃ��A�Q�O�Q�T�Ԗڂɂ��鐔�����߂�B
�@�@�܂��A�P�Ԗڂ���Q�O�Q�T�Ԗڂ܂ł̐��̂����A[��]���T�ƂȂ鐔�͉����邩�B
�i���j�@�P����P�O�O�܂ł̐����̂����A��������[��] �ƂȂ鐮���͉����邩�B
�i���j�i�C�j�@���������R�ł���P�ȏ�̐������́A�@�����S���{�R�@�i�����O�A�P�A�E�E�E�j�Ə�����B
����āA�Q�O�Q�T�Ԗڂ̐��́A�@�S�~�Q�O�Q�S�{�R���W�O�X�X
�@�����S���{�R���V���{�T�@���A�@�S�����V���{�Q�@�Ȃ̂ŁA�@�S�E�S���V�E�Q�{�Q�@���A
�@�S�i���|�S�j���V�i���|�Q�j�@����A���|�S���V���@�i���͐����j�@�Ə�����B
�@����āA�@�����S�i�V���{�S�j�{�R���Q�W���{�P�X
�@�P�X���Q�W���{�P�X���W�O�X�X�@���A�@�O�������Q�W�W�@�Ȃ̂ŁA���߂���́A�Q�W�X��
�i���j�@�\�ɂ܂Ƃ߂āA
| �� |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
| ������ |
1 |
2 |
3 |
0 |
1 |
2 |
3 |
0 |
1 |
2 |
3 |
0 |
1 |
2 |
3 |
0 |
1 |
2 |
3 |
0 |
1 |
2 |
3 |
0 |
1 |
2 |
3 |
0 |
| [��] |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
�@�����Q�W���ɍl���āA�P�O�O���Q�W�~�R�{�P�U�@���A
�@���߂���́A�@�S�~�R�{�R���P�T�i�j�@�@�i�I�j
�U�m�`�n�i�P�j�@�@���}�̂悤�ɁA���^�̃��C�g���V�g�ݍ��킹�āA�P�̑��u��������B����
�@�@����̃��C�g��������A�������肷�邱�ƂŁA���낢��ȋL����\����B�������A���u��
�@�@��]��������A���Ԃ����肷�邱�Ƃ͂��Ȃ��B
�@�@
�@�V�̃��C�g�̂����A�ǂ����Q�̃��C�g���̏Ⴕ�Ă��܂����B�̏Ⴕ�����C�g�͂��Ȃ��B��
�}�̂悤�ȋL�����\�ꂽ�Ƃ��A�{���\�����Ƃ����L���Ƃ��čl��������̂͑S���ʼn��ʂ�
���邩�B�������A���́A���C�g�����Ă����ԁA���́A���C�g�������Ă����Ԃ�\���B
�@�@
�i�Q�j�@�i�P�j�Ɠ����`�������ʂ̑��u��������B������̑��u�͂��ꂼ��̃��C�g�ɂ��āA��
�@�F�̃��C�g������A�F�̃��C�g������A���C�g�����Ȃ��A�̂R�ʂ�̑�������邱��
�@���ł���B�������A�i�P�j�Ɠ����悤�ɁA���u����]��������A���Ԃ����肷�邱�Ƃ͂��Ȃ��B
�@�@�\����L���͑S���ʼn���ނ��邩�B�������A���ׂẴ��C�g�������Ă����Ԃ��P��ނ�
�@�����邱�Ƃɂ���B
�A�@�V�̃��C�g�̂����A�ǂ����Q�̃��C�g���̏Ⴕ�Ă��܂����B�̏Ⴕ�����C�g�́A�ԐF����
�@���悤�Ƃ���ƐF�����A�F�����悤�Ƃ��Ă����C�g�͂��Ȃ��B
�@���}�̂悤�ȋL�����\�ꂽ�Ƃ��A�{���\�����Ƃ����L���Ƃ��čl��������̂͑S���ʼn���
�ނ��邩�B
�@�@
�i���j�i�P�j�@�̏Ⴕ���Q�̃��C�g�̑I�ѕ��́A4�b2���U�i�ʂ�j
�@�̏Ⴕ���P�̃��C�g�̑I�ѕ��́A�S�ʂ�
�@�̏�Ɋւ�炸���C�g��I�Ȃ��ꍇ�́A�P�ʂ�
�@�ȏォ��A���߂�ꍇ�̐��́A�@�U�{�S�{�P���P�P�i�ʂ�j
�i�Q�j�@�@�R7���Q�P�W�V�i�ʂ�j
�A�@�F�̃��C�g�̂����Q���̏Ⴕ�Ă���ꍇ�A���̏ꍇ�̐��́A�R�ʂ�
�@�F�̃��C�g�̂����P���̏Ⴕ�Ă���ꍇ�A�c���̃��C�g���̏Ⴕ�Ă���̂ŁA
�@�I�ѕ��́A�R�~�i�S�{�P�j���P�T�i�ʂ�j
�@�F�̃��C�g�ȊO�łQ�̏Ⴕ�Ă���ꍇ�́A�i�P�j���A�P�P�ʂ�
�@�ȏォ��A���߂�ꍇ�̐��́A�@�R�{�P�T�{�P�P���Q�X�i�ʂ�j�@�@�i�I�j
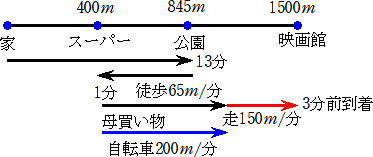
�V�@�@������͉Ƃ���P�T�O�O����ɂ���f��قɁA�f������ɍs���܂��B��f�J�n�̂P�O��
�@�@�O�ɓ�������悤�A�����ĉƂ��o�����܂����B
�@�@
�@�o�����Ă���P�R����A�����̑O�Ń`�P�b�g��Y�ꂽ���ƂɋC�����A�����ĉƂւƈ����Ԃ�
�܂������A�Ƃ���S�O�O���̂Ƃ���ɂ���X�[�p�[�̑O�ŁA�`�P�b�g��͂��ɂ��Ă��ꂽ���ꂳ��
�Əo��܂����B
�@������̓`�P�b�g�����A���ꂳ��Əo����Ă���P����ɁA�Ăщf��قւƕ����ďo
�����܂����B�����������Ƃ���ŁA��f�J�n�ɒx�ꂻ���Ȃ��ƂɋC�����A�c��̓��𑖂��
�����B���̌��ʁA��f�J�n�̂R���O�ɉf��قɒ����܂����B
�@������̕��������͕����U�T���A���鑬���͕����P�T�O���ł��B
�i�P�j�@�������ꂳ��Əo������̂́A�Ƃ��o�Ă��牽����ł����B
�i�Q�j�@������͉����ԑ���܂������B
�i�R�j�@���ꂳ��́A�����Ăяo��������A�X�[�p�[�Ŕ����������Ă���A���]�Ԃɏ����
�@�����i�����ւƌ������܂��B���]�Ԃ̑����͕����Q�O�O���ł��B��������n��
�@��܂łɁA���ꂳ������ɒǂ������߂ɂ́A�����ȓ��ɔ��������ς܂�������ł�
�@���B
�i���j�@�P�T�O�O���U�T���R�O�O/�P�R�@���A�f��̏�f�J�n�́A�o������
�@�R�O�O/�P�R�{�P�O���S�R�O/�P�R�i����j
�i�P�j�@�Ƃ�������܂ł̋����́A�U�T�~�P�R���W�S�T�i���j�@�ŁA�S�S�T�������āA���ꂳ��Əo���
�����ƂɂȂ�B����āA�������ꂳ��Əo������̂́A�Ƃ��o�Ă���
�@�i�W�S�T�{�S�S�T�j���U�T���Q�T�W/�P�R�i����j
�i�Q�j�@������́A��������f��ق܂łP�P�O�O�����ŏ������A�r�����瑖�����B�f��قɒ�����
�łɗv�������Ԃ́A�@�S�R�O/�P�R�|�Q�T�W/�P�R�|�P�|�R���P�Q�O/�P�R�i���j
�@�������������Ԃ� �� ���Ƃ���ƁA
�@�@�U�T�E�i�P�Q�O/�P�R�|���j�{�P�T�O�����P�P�O�O�@���A�@�����P�O�O/�P�V
�@����āA�������������Ԃ́A�P�O�O/�P�V����
�i�R�j�@���ꂳ�X�[�p�[�Ŕ��������Ă������Ԃ� �� ���Ƃ���ƁA��������n�߂�܂ł�
���Ԃ́A�@�P�Q�O/�P�R�|�P�O�O/�P�V���V�S�O/�Q�Q�P�@�Ȃ̂ŁA���������������́A
�@�V�S�O/�Q�Q�P�E�U�T���R�V�O�O/�P�V
����āA�i�V�S�O/�Q�Q�P�|���j�E�Q�O�O���R�V�O�O/�P�V�@���A�@�����X�X�X/�S�S�Q�i���j
�@�ȏォ��A���ꂳ��͍�����ɒǂ������߂ɁA�X�X�X/�S�S�Q���ȓ��ɔ��������ς܂����
�悢�B�@�@�i�I�j
�i�R�����g�j�@���ݒ�͒P�������A�����v�Z����ςł����B
�W�@�܂̒��ɏd���P�O�P���̐ԋʂ��P�O�A�d���P�O�O���̐ԋʂ��S�A�d���P�O�O���̔��ʂ��U��
�@�����Ă���B�܂̒��ł́A�ǂ̋ʂ���ʏo���Ȃ����̂Ƃ���B
�@���̑܂̒�����A�����ɂS�̋ʂ����o���B���o�����S�̋ʂ̐F�������Ƃ��́A����
�ȏ�ʂ����o���Ȃ��B�����łȂ��Ƃ��́A���o�����ʂ͑܂ɖ߂����A������x�܂̒�����
�S�̋ʂ����o���B���o�����S�̋ʂ̐F�������Ƃ��́A����ȏ�ʂ����o���Ȃ��B
�����łȂ��Ƃ��́A���o�����ʂ͑܂ɖ߂����A������x�܂̒�����S�̋ʂ����o���B
�@���̂悤�ɁA�S�̋ʂ����o����Ƃ����肩�����B�S�Ă̋ʂ����o�����Ƃ����A��Ƃ��I
����B
�@�P��ڂɎ��o�����̂́A�ԋʂQ�Ɣ��ʂQ�ŁA���̏d���̕��ς͂P�O�O�{�P/�S���ł������B
�i�P�j�@�S�̋ʂ��T����o���āA��Ƃ��I�����B
�@�@�P��ڂ���T��ڂ܂ł̊e��Ŏ��o�����S�̋ʂ̏d���̕��ς̕��ς͉�g���B
�A�@�T��ڂŎ��o�����ʂ̏d���̕��ς́A�P��ڂŎ��o�����ʂ̏d���̕��ψȉ��ł����B
�@�T��ڂɎ��o�����S�̋ʂ̐F�ƁA���̂S�̋ʂ̏d���̕��ςƂ��čl������g�ݍ���
�@����S����B
�i�Q�j�@�S�̋ʂ��R����o���āA��Ƃ��I�����B�Ō�Ɏ��o�����ʂ̏d���̕��ς�
�@�P�O�O�{�P/�S���̂Ƃ��A�܂̒��Ɏc�����ʂ̏d���̍��v�́A��ԏd���ĉ�g�A��Ԍy���ĉ�g��
�@�Ȃ邩�B
�i���j�@��ӂ��A�P��ڂɎ��o�����̂́A�d���P�O�P���̐ԋʂ��P�A�d���P�O�O���̐ԋʂ��P
�@�A�d���P�O�O���̔��ʂ��Q�̌v�S�ł���B�Q��ڈȍ~�́A�c��́A
�@�d���P�O�P���̐ԋʂ��X�A�d���P�O�O���̐ԋʂ��R�A�d���P�O�O���̔��ʂ��S�ƂȂ�B
�i�P�j�@�@�S�̋ʂ��T����o���āA��Ƃ��I�����̂ŁA�ʂ̏d���̕��ς́A
�@�i�P�O�P�~�P�O�{�P�O�O�~�S�{�P�O�O�~�U�j/�Q�O���Q�O�P/�Q�i���j
�A�@�T��ڂŎ��o�����ʂ̏d���̕��ς́A�P��ڂŎ��o�����ʂ̏d���̕��ψȉ��Ƃ�����
�@�Ƃ���A�P�O�O���@�܂��́@�P�O�O�{�P/�S��
�@�T��ڂŏI���Ȃ̂ŁA�@�Q��ځ`�T��ڂŔ��ʂ��P���g�����A�Q��ځ`�S��ڂŔ��ʂ�
�g����A�Ō�̂T��ڂ͐ԋʂ݂̂̏ꍇ���N���蓾��B
���̂Ƃ��A�T��ڂɎ��o�����S�̋ʂ̐F�Əd���̕��ς̉\���́A
�@�ԂP�O�O���R�{���P�O�O���P�E�E�E�d���̕��ρ@�P�O�O��
�@�ԂP�O�P���P�{�ԂP�O�O���Q�{���P�O�O���P�E�E�E�d���̕��ρ@�P�O�O�{�P/�S��
�ԋʂ��R�����g���Ȃ��̂ŁA
�@�ԂP�O�P���P�{�ԂP�O�O���R�{���P�O�O���O�E�E�E�d���̕��ρ@�P�O�O�{�P/�S��
�i�Q�j�@�P��ځ@�ԂP�O�P���P�{�ԂP�O�O���P�{���P�O�O���Q��
�@�Q���
�@�R��ڂŏI���Ƃ������Ƃ́A�R��ڂɐԋʂS�@�܂��́@���ʂS�@�o���Ƃ������ƁB
������ɁA���ʂ��U�����Ȃ��̂ŁA�Q��ڂɏI�����Ă��܂��B����͖����ł���B
�@����āA�R��ڂ́A�ԂP�O�P�����P�{�ԂP�O�O�����R�@�ƂȂ�B
���̂Ƃ��A�Q��ڂɎg����̂́A
�@�d���P�O�P���̐ԋʂ��W�A�d���P�O�O���̐ԋʂ��O�A�d���P�O�O���̔��ʂ��S�ƂȂ�B
�@�c��̋ʂ̏d�����ő�ɂȂ�̂́A
�@�Q��ڂ��A�@�ԂP�O�P���P�{���P�O�O���R�@�̂Ƃ��Ȃ̂ŁA�c��̏d���́A
�@�@�P�O�P�~�V�{�P�O�O�~�P���W�O�V�i���j
�@�c��̋ʂ̏d�����ŏ��ɂȂ�̂́A
�@�Q��ڂ��A�@�ԂP�O�P���R�{���P�O�O���P�@�̂Ƃ��Ȃ̂ŁA�c��̏d���́A
�@�@�P�O�P�~�T�{�P�O�O�~�R���W�O�T�i���j�@�@�i�I�j
�i�NjL�j�@�ߘa�V�N�Q���T���i���j�t�������V�������ɗߘa�V�N�x�J�����w������肪�f��
�@�@�@���ꂽ�B���������肪�������̂Œ��킵�Ă݂��B�i�ꕔ����j
��P��i�Q�j�@�ĕ��N�͂����炩�̂������������Ă���B�܂��A�������̂P/�X���Q�O�~������
�@�@�iA���܂����B���ɁA�c���̂P/�V���S�O�~�������iB���܂����B�����āA���̂�
�@�@���̎c���̂P/�T���P�O�~�������iC�����Ƃ���A�Ō�Ɏc���������͂͂��߂̏���
�@�@���̂S�����S�W�O�~���������B���iA�̒l�i�����߂�B
�i���j�@���iA�A�a�A�b�̒l�i�����ꂼ��A�A�a�A�b�Ƃ���B�܂��A�ĕ��N�̏��������m�Ƃ����B
��ӂ��A�@�m/�X�|�Q�O��A�A�i�m�|A�j/�V�|�S�O���a�A�i�m�|A�|�a�j/�T�|�P�O���b�@�ŁA
�@�m�|A�|�a�|�b���i�Q/�T�j�m�{�S�W�O
�������A�@�m�|A�|�a�|�b���S�b�{�T�O���i�Q/�T�j�m�{�S�W�O�@����A�@�P�O�b���m�{�P�O�V�T
���Ȃ킿�A�b���i�P/�P�O�j�m�{�Q�P�T/�Q
�܂��A�@�m�|A�|�a���U�a�{�Q�W�O�@����A�@�T�b�{�T�O���U�a�{�Q�W�O�@����A�U�a���T�b�|�Q�R�O
����āA�U�a���i�P/�Q�j�m�{�P�O�V�T/�Q�|�Q�R�O���i�P/�Q�j�m�{�U�P�T/�Q�@���A
�@�a���i�P/�P�Q�j�m�{�Q�O�T/�S
���̂Ƃ��A�@�m�|A�|�Q�W�O���V�a���i�V/�P�Q�j�m�{�P�S�R�T/�S�@���A�@�i�T/�P�Q�j�m�|A���Q�T�T�T/�S
����āA�@�m�|�i�P�Q/�T�jA���P�T�R�R
�Ƃ���ŁA�@�m�|�XA���P�W�O�@�Ȃ̂ŁA�@�i�R�R/�T�jA���P�R�T�R�@���A�@A���Q�O�T�i�~�j�@�@�i�I�j
�i�R�����g�j�@�S���A���P���������̉�@�́A�ʂ����ď��w�����x���Ȃ̂��낤���H
�i�NjL�j�@�ߘa�V�N�Q���Q�S���t��
�@��L�̖��ŁA�Q�O�Q�T�N�Ƃ������Ƃ���A���̂悤�ɉ������������������D�D�D�B
�@�ĕ��N�̏��������u�Q�O�Q�T�~�v�Ƃ���ƁA���i�`�̒l�i�́A�`���Q�O�Q�T/�X�|�Q�O���Q�O�T�i�~�j
����ƁA�c���́A�P�W�Q�O�~�Ȃ̂ŁA���i�a�̒l�i�́A�@�P�W�Q�O/�V�|�S�O���Q�Q�O�i�~�j
���̂Ƃ��A�c���́A�P�U�O�O�~�Ȃ̂ŁA���i�b�̒l�i�́A�@�P�U�O�O/�T�|�P�O���R�P�O�i�~�j
�Ō�Ɏc���������́A�P�Q�X�O�~�A�͂��߂̏������Q�O�Q�T�~�̂S���́A�W�P�O�~�Ȃ̂ŁA����
���S�W�O�~�����B���������āA�����������藧�̂ŁA���i�`�̒l�i�́A�`���Q�O�T�i�~�j
�@���̂悤�Ȍv�Z�̂悤�ɁA�c���ɒ��ڂ���ƁA���ȒP�ɋ��߂��邩������Ȃ��B
�i�ʉ��j�@�ĕ��N�̏��������u�P�v�Ƃ��āA���iA�w����̎c���́A�@�u�W/�X�v�{�Q�O
�@���i�a�w����̎c���́A�@�i�u�W/�X�v�{�Q�O�j�~�i�U/�V�j�{�S�O���u�P�U/�Q�P�v�{�S�O�O/�V
�@���i�b�w����̎c���́A�@�i�u�P�U/�Q�P�v�{�S�O�O/�V�j�~�i�S/�T�j�{�P�O���u�U�S/�P�O�T�v�{�R�X�O/�V
����āA�@�u�U�S/�P�O�T�v�{�R�X�O/�V���u�Q/�T�v�{�S�W�O�@���A�@�u�Q�Q/�P�O�T�v���Q�X�V�O/�V
���������āA�@�u�P�v���i�Q�X�V�O/�V�j�~�i�P�O�T/�Q�Q�j���Q�O�Q�T�@���A
�@���i�`�̒l�i�́A�`���Q�O�Q�T/�X�|�Q�O���Q�O�T�i�~�j�@�@�i�I�j
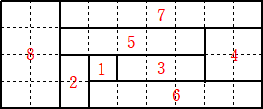
��Q���@�����Ԋu�ŁA�c�S�s�~���R�X��̖ڐ��肪�����ꂽ������B���̔�ڐ����
�@�@�����ĂW�̒����`�ɋ��B
�@�����`�́A�ӂ��܂��}�X�ڂ̌����P�A�Q�A�R�A�S�A�T�A�U�A�V�A�W�̂��̂��P������悤
�ɂ���B�Ȃ��A�Ⴆ�A�S�}�X�̒����`�̏c�~���́A�P�~�S�A�Q�~�Q�A�S�~�P�̂�����ł�����
��Ȃ��B
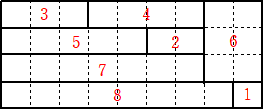
�@���̂Ƃ��A�s���Ƃɒ����`������ނ��邩�𐔂��A�ォ�� �� �s�ڂ� �� ��ނ���Ƃ��A�� �� ��
�̐ς��v�Z����B�����āA���̒l���P�s�ڂ���S�s�ڂ܂ʼn����������|�C���g�Ƃ���B
�i�P�j�@���̍����}�A�E���}�̋����̃|�C���g�����ꂼ�ꓚ����B
| �@ |
 |
�@ |
 |
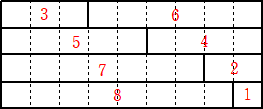
�i�Q�j�@�|�C���g���Q�O�A�R�O�ƂȂ���������ꂼ��P��������B
�i�R�j�@�|�C���g���Ȃ�ׂ��傫���������P������B�܂��A���̃{�C���g����B
�i���j�i�P�j�@�����}�̃|�C���g�́A�@�P�~�R�{�Q�~�R�{�R�~�Q�{�S�~�Q���Q�R
�@�E���}�̃|�C���g�́A�@�P�~�Q�{�Q�~�R�{�R�~�T�{�S�~�R���R�T
�i�Q�j�@�|�C���g���Q�O�ƂȂ�����E�E�E�i�P�j�̍������Q�l�ɂ��āA
�@�@
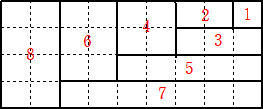
�|�C���g���R�O�ƂȂ����
�@�@
�i�R�j�@�Ⴆ�A
�@�@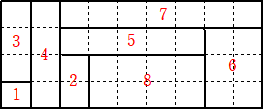
�@��}�̃|�C���g�́A�@�P�~�R�{�Q�~�S�{�R�~�T�{�S�~�T���S�U�@�@�i�I�j
�i�R�����g�j�@���ꂪ�ő�Ƃ������M�͑S���Ȃ��B
��S���@���O�p�`���ʂƂ���O�p��PQR-STU�����镽�ʂŐؒf���āA���̐ؒf�ʂ��l��
�@�@��B�Ȃ��A���}�̂悤�ɁA�O�p��P QR-ST U�͒����`QTUR���ʂɂ��Ēu���Ă���B
�@�@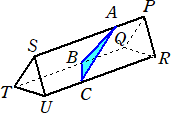
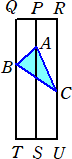
�@�q�J�����ؒf����ƁA�ؒf�ʂ͎O�p�`�ƂȂ�A������O�p�`ABC�Ƃ���B���̂Ƃ��A�O
�p��PQR-STU��^�ォ�猩��ƁA���}�̂悤�ɁA�pA���X�O�x�A�pB���U�O�x�A�pC���R�O�x��
�������B
�@�@
�@�O�p�`ABC�̎��ۂ̌`��m�邽�߁A�q�J������͎��̂悤�ɍl�����B
�@�����Ă����AB�ABC�ACA�̂����A���ۂ̒����ɓ������͕̂�BC�݂̂ŁA���̂Q�ӂ͎���
�ɂ͂����ƒ����͂��B
�@�܂��A��BC�̒�������ӂƂ��鐳�O�p�`���l����ƁA���̍�����QR�̒����ɓ������B
����āA��QR��p���āA��BC����}�ł���B
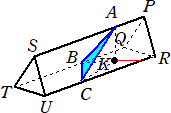
�@���ɁA���}�̂悤�ɁA����BC��ɓ_H���Ƃ�A���� AH�ƒ���BC�������ɂȂ�悤�ɂ���B
����ƁAAH�̒����Ɠ_H�̈ʒu���킩��A�O�p�`ABC�̎��ۂ̌`���킩��B
| �@ |
 |
�@ |
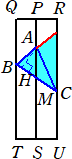 |
�@�����ŁA�_A��ʂ蕽��QTUR�ɐ����Ȓ����ƕ��� QTUR�Ƃ̌�_��K�Ƃ���B�^�ォ�猩
��Ɠ_A�Ɠ_K���d�Ȃ��Č�����̂ŁA�O�p�`KBC�ɂ����ĊpK�́i�@�C�@�j�x�A�p�a�́i�@���@�j
�x�A�pC�́i�@�n�@�j�x�ł���B
�@����HK�ƒ���BC�͐����Ɍ�����Ă���̂ŁAHK�̒�����CK�̒����́i�@�j�@�j�{�ł���B
�@�܂��A��BC�̐^�̓_��M�Ƃ���ƁA�^�ォ�猩��ƎO�p�`ABM�́i�@�z�@�j�O�p�`�Ɍ�
����̂ŁA�O�p�`KBM���i�@�z�@�j�O�p�`�ł���AHC�̒�����HB�̒����́i�@�w�@�j�{�ł���B
�܂��AHK�̒�����QR�̒����́i�@�g�@�j�{�ŁAAK�̒����͐��O�p�`PQR�̍����ɓ������B
�@����ŎO�p�`AHK�̌`���킩��A����𗘗p���ĎO�p�`ABC�̎��ۂ̌`���킩��B
���̂Ƃ��A��̕��͂̋���i�@�C�@�j�`�i�@�g�@�j�ɓK�Ȍ��܂��͐��l����B
�i���j�@�_A��ʂ蕽��QTUR�ɐ����Ȓ����ƕ��� QTUR�Ƃ̌�_��K�Ƃ���B�^�ォ�猩���
�_A�Ɠ_K���d�Ȃ��Č�����̂ŁA�O�p�`KBC�ɂ����ĊpK�́i�X�O�j�x�A�p�a�́i�U�O�j�x�A�pC
�́i�R�O�j�x�ł���B
�@����HK�ƒ���BC�͐����Ɍ�����Ă���̂ŁAHK�̒�����CK�̒����́i�P/�Q�j�{�ł���B
�@�܂��A��BC�̐^�̓_��M�Ƃ���ƁA�^�ォ�猩��ƎO�p�`ABM�́i���j�O�p�`�Ɍ�����
�̂ŁA�O�p�`KBM���i���j�O�p�`�ł���AHC�̒�����HB�̒����́i�R�j�{�ł���B
�܂��AHK�̒�����QR�̒����́i�P/�Q�j�{�ŁAAK�̒����͐��O�p�`PQR�̍����ɓ������B�i�I�j
�@�@�ȉ��A�H�����I