タを用いれば、数値的にはあっという間で答えてくれますが、この数値を明示式で表したい
時にはこの手が使えない。
そこで、手計算を駆使して、我慢強くコツコツと進めることで、この I の座標を明示式で見つ
けてみて欲しい。
(コメント) 「複素数の底力」によれば、
単位円周上の2点A(α2)、B(β2) (ただし、0≦argα<argβ<π) とすると、
劣弧ABの中点M(αβ)、優弧ABの中点M’(−αβ) と表せる。
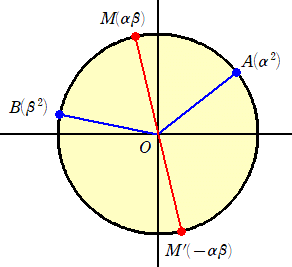
以上の準備のもとに、単位円周上の3点A(α2)、B(β2)、C(γ2) をとる。
(ただし、0≦argα、argβ<π、π≦argγ<2πとする。)
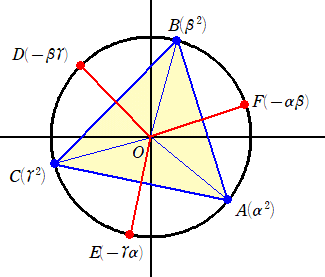
このとき、弧BC、CA、ABの中点をそれぞれD、E、Fとおくと、
D(−βγ) 、E(−γα) 、F(−αβ)
となる。∠Aの2等分線ADの方程式は、
(z+βγ)/(α2+βγ)=(
すなわち、 z+βγ=α2(βγ
同様にして、∠Bの2等分線Eの方程式は、 z+γα=β2(γα
(1)×β−(2)×α より、 (β−α)z+γ(β2−α2)=αβ(α−β)
α≠β より、 z+γ(α+β)=−αβ なので、 z=−αβ−βγ−γα
これが、内心の座標を表す。
このことを活用すれば、内心の座標は求められるのでは...。でも、計算が大変そう。
DD++ さんからのコメントです。(令和6年9月16日付け)
AI と BC の交点を D とすると、
BD : CD = BA : AC = √50 : √80 = √5 : 2√2 = (-5+2√10) : (8-2√10)
よって、 D ( (38-2√10)/3, (43-10√10)/3 ) より
AI : ID = AB : BD = √50 : (-5+8√10)√26/3
あとはこれを内分点の公式につっこんで整理すればいいはず……ですが、数字が大きくな
りすぎるのでギブアップ。
らすかるさんからのコメントです。(令和6年9月16日付け)
A(a,b)、B(c,d)、C(e,f) とすると、
直線ABは、(d-b)x-(c-a)y-(ad-bc)=0
直線BCは、(f-d)x-(e-c)y-(cf-de)=0
直線CAは、(b-f)x-(a-e)y-(eb-fa)=0
直線ABから k 離れた直線は、(d-b)x-(c-a)y-(ad-bc)-k√{(d-b)^2+(c-a)^2}=0 … (1)
直線BCから k 離れた直線は、(f-d)x-(e-c)y-(cf-de)-k√{(f-d)^2+(e-c)^2}=0 … (2)
直線CAから k 離れた直線は、(b-f)x-(a-e)y-(eb-fa)-k√{(b-f)^2+(a-e)^2}=0 … (3)
(1)(2)から k を消去して、
{(f-d)√{(d-b)^2+(c-a)^2}-(d-b)√{(f-d)^2+(e-c)^2}}x
-{(e-c)√{(d-b)^2+(c-a)^2}-(c-a)√{(f-d)^2+(e-c)^2}}y
=(cf-de)√{(d-b)^2+(c-a)^2}-(ad-bc)√{(f-d)^2+(e-c)^2} … (4)
(2)(3)から k を消去して、
{(b-f)√{(f-d)^2+(e-c)^2}-(f-d)√{(b-f)^2+(a-e)^2}}x
-{(a-e)√{(f-d)^2+(e-c)^2}-(e-c)√{(b-f)^2+(a-e)^2}}y
=(eb-fa)√{(f-d)^2+(e-c)^2}-(cf-de)√{(b-f)^2+(a-e)^2} … (5)
(4)(5)から y を消去して整理すると、
x={a√{(f-d)^2+(e-c)^2}+c√{(b-f)^2+(a-e)^2}+e√{(d-b)^2+(c-a)^2}}
/{√{(f-d)^2+(e-c)^2}+√{(b-f)^2+(a-e)^2}+√{(d-b)^2+(c-a)^2}}
(4)(5)から x を消去して整理すると、
y={b√{(f-d)^2+(e-c)^2}+d√{(b-f)^2+(a-e)^2}+f√{(d-b)^2+(c-a)^2}}
/{√{(f-d)^2+(e-c)^2}+√{(b-f)^2+(a-e)^2}+√{(d-b)^2+(c-a)^2}}}
よって、A(a,b)、B(c,d)、C(e,f)を頂点とする内心の座標は、
(
{a√{(f-d)^2+(e-c)^2}+c√{(b-f)^2+(a-e)^2}+e√{(d-b)^2+(c-a)^2}}
/{√{(f-d)^2+(e-c)^2}+√{(b-f)^2+(a-e)^2}+√{(d-b)^2+(c-a)^2}}
,
{b√{(f-d)^2+(e-c)^2}+d√{(b-f)^2+(a-e)^2}+f√{(d-b)^2+(c-a)^2}}
/{√{(f-d)^2+(e-c)^2}+√{(b-f)^2+(a-e)^2}+√{(d-b)^2+(c-a)^2}}}
)
見やすいように、
√{(f-d)^2+(e-c)^2}=BC、√{(b-f)^2+(a-e)^2}=CA、√{(d-b)^2+(c-a)^2}=AB と書けば、
内心の座標は、
((aBC+cCA+eAB)/(BC+CA+AB),(bBC+dCA+fAB)/(BC+CA+AB))
A(3,2)、B(10,1)、C(11,6)の場合は、
BC=√{(6-1)^2+(11-10)^2}=√26、CA=√{(2-6)^2+(3-11)^2}=4√5、AB=√{(1-2)^2+(10-3)^2}=5√2
なので、内心の座標は、
((3√26+40√5+55√2)/(√26+4√5+5√2),(2√26+4√5+30√2)/(√26+4√5+5√2))
=((124+25√10-10√13-√130)/18,(76-5√10+20√13-7√130)/18)
※有理化にはWolframAlphaを使いました。
GAI さんからのコメントです。(令和6年9月16日付け)
DD++ さんの
D ( (38-2√10)/3, (43-10√10)/3 ) は、D( (25+2√10)/3.(10√10-22)/3 ) に
AI : ID = AB : BD = √50 : (-5+8√10)√26/3 は、
AI : ID = AB : BD = √50 : (-5+2√10)√26/3
となりませんか?
らすかるさんの
((124+25√10-10√13-√130)/18,(76-5√10+20√13-7√130)/18)
※有理化にはWolframAlphaを使いました。
について、方法は異なりますが、最終結果は同じになっています。
(コンピュータで数値だけ求めたい時はこの式を利用していました。)
有理化もコツコツ進めて行きました。(すごく面倒でした。)
DD++ さんからのコメントです。(令和6年9月16日付け)
そうかもしれません。内分比をうっかり逆にしてたかも?なんにせよ、この計算は暗算でや
るもんじゃないですね……。
以下、工事中!
