・偽造金貨の特定 Dengan kesaktian Indukmu 氏
「放射性物質を含む偽造金貨の特定:技術者とガイガーカウンターによる測定戦略」
クソ暑い夏休みに英語の補習を受講しに登校していたことを思い出しました。
たまには英文で。
There are eight gold coins, one of which is a forgery containing radioactive material. The
task is to identify this forgery using a series of measurements conducted
by technicians with
Geiger counters. The problem is structured as follows:
1. Coins: There are 8 gold coins, numbered 1 through 8. Exactly one coin is a forgery.
2. Forgery Characteristics: The forged coin contains radioactive material,
detectable by a
Geiger counter.
3. Technicians: There are 10 technicians available to perform measurements.
4. Measurement Process:
Each technician selects a subset of the 8 coins for measurement.
The technician uses a Geiger counter to test the selected coins simultaneously.
The Geiger counter reacts if and only if the forgery is among the selected coins.
Only the technician operating the device knows the result of the measurement.
5. Measurement Constraints:
Each technician performs exactly one measurement.
A total of 10 measurements are conducted.
6. Reporting:
After each measurement, the technician reports either "positive"
(radioactivity detected)
or "negative" (no radioactivity detected).
7. Reliability Issue: Up to two technicians may provide unreliable reports,
either due to
intentional deception or unintentional error.
8. Objective: Identify the forged coin with certainty, despite the possibility of up to two
unreliable reports.
Challenge
The challenge is to design a measurement strategy and analysis algorithm
that can
definitively identify the forged coin, given these constraints and potential inaccuracies in
the technicians' reports.
(コメント) 翻訳してみました!
金貨が 8 枚あり、そのうち 1 枚は放射性物質を含む偽造品です。この偽造品を、ガイガー
カウンターによる測定によって特定することが問題です。手順は次の通りです。
1.金貨が 8 枚あり、1 から 8 まで番号が付けられています。偽造品は 1 枚だけです。
2.偽造金貨には放射性物質が含まれており、ガイガーカウンターで検出できます。
3.測定を実行できる技術者は 10 人います。
4.各技術者は、測定する 8 枚の金貨からいくつかを選択します。ガイガーカウンターを使
用して、選択した金貨を同時に測定します。ガイガーカウンターは、選択した金貨の中に
偽造品がある場合にのみ反応します。測定する技術者だけが、測定結果を知ります。
5.各技術者は、1 回だけ測定を実行します。合計 10 回の測定が行われます。
6.各測定後、技術者は「陽性」(放射能が検出された) または「陰性」(放射能が検出されな
かった) のいずれかを報告します。
7.意図的な欺瞞または意図しない誤りにより、最大 2 人の技術者が信頼できない報告を行
う可能性があります。
8.最大 2 つの信頼できない報告がある可能性にもかかわらず、偽造金貨が確実に識別で
きます。
これらの制約と技術者の報告の潜在的な不正確さを考慮して、偽造金貨を確実に識別で
きる測定方法を考えてください。
DD++ さんからのコメントです。(令和6年9月9日付け)
10人いたら簡単だとして、9人解ができそうでできない……。必要な最少人数って何人なん
でしょうね?
Dengan kesaktian Indukmu さんからのコメントです。(令和6年9月10日付け)
DD++さんにとっては 10人は簡単…… うお。
9人解の探索をしようと思い、ファノ平面は使えないかと思いつきまして。
"000 000 000 ", 0,0,0,
"110 011 101 ", 6,3,5,
"111 110 001 ", 7,6,1,
"010 100 110 ", 2,4,6,
"011 001 010 ", 3,1,2,
"100 111 011 ", 4,7,3,
"001 101 100 ", 1,5,4,
"101 010 111 ", 5,2,7
これ、使えませんし、ここになにか1ビットを追加してもどうにもならないのでした。
たとえば、
"010 100 110 ", 2,4,6,
"011 001 010 ", 3,1,2,
"001 101 100 ", 1,5,4,
の部分だけでも、1ビットを増やしたくらいでは、2人の嘘つきを確定できません。
DD++ さんからのコメントです。(令和6年9月10日付け)
はい、10人なら簡単です。9人の場合も、嘘つきが「確定2人」なら可能なんですけどねえ……。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年9月10日付け)
「確定2人」というお言葉に驚きました。探したのですが、見つからず、です。
副産物として、以下の通りの変なものを見つけました。
3 ビットの 7 つの数を数珠つなぎにします。
" 100 111 010 110 001 011 101 "
数珠ですので、最後尾の 101 の次には 先頭の 100 につながることとします。
この数珠の、三連続する数の組みは、7通りあるわけですが、それぞれの組のなかの3つ
の数を XOR 演算すると、被らずに 001 から 111 までが漏れなく勢揃いします。(下記参照)
onst codes = [
"100 111 010 ", // XOR結果 001
"111 010 110 ", // XOR結果 011
"010 110 001 ", // XOR結果 101
"110 001 011 ", // XOR結果 100
"001 011 101 ", // XOR結果 111
"011 101 100 ", // XOR結果 010
"101 100 111 ", // XOR結果 110
];
この結果は、よくわかりませんが、いわゆる魔円陣のバリエーションですね。
さて、上の一覧を、「放射能検査のために9人それぞれに割り当てる金貨の一覧(但し、0を
ガイガーカウンターではかる印とし、一覧にはないが全員がはかる金貨も1枚ある)」と見立
てると……。
ほんとに惜しいんです。残りのひとりの10番目の技術者が検査すれば偽造金貨は見つかる
のですけれど。
うーん残念。あとひとりをどうしても省力化したいのですが。
DD++ さんからのコメントです。(令和6年9月10日付け)
9人で、嘘つきが確定2人の場合の手順は、以下です。
まず、
1人目と2人目:1,2,3,4 、3人目と4人目:1,2,5,6 、5人目と6人目:1,3,5,7 と測定します。
うち1回でも2人から不一致な報告された場合は、7人目と8人目にそれ(のうちの1つ)と同じ
測定してもらいます。
不一致な報告が一度でもあったなら、2人が一致した報告は全て信頼できるので、これで、
・上記3パターンの信頼できる結果が出揃っている
・上記3パターンのうち2パターンの信頼できる結果があり、9人目が正直者確定
のいずれかになっています。
前者はすでに偽物確定、後者は結果が得られていないものを9人目に頼めばいいです。
3組全てで一致する結果が報告された場合、例えば全て放射線検出されたと報告された場
合は、以下の4つの可能性があります。
(他のパターンも番号が変わるだけで論理は同じ実質同じ)
・1が偽物で、残り3人に「確定で2人」嘘つきがいる
・2が偽物で、残り3人に嘘つきはいない
・3が偽物で、残り3人に嘘つきはいない
・5が偽物で、残り3人に嘘つきはいない
この場合、残り3人に、2と3と5をそれぞれ単体で調べてもらいます。
1人だけが放射線検出を報告した場合、その人の調べたコインが偽物です。(※)
2人が放射線検出を報告した場合、その2人が嘘つきで、1が偽物です。
嘘つきが「最大で2人」の場合、※のところで1が偽物で嘘つきが1人しかいなかった可能性
が消し切れません。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年9月10日付け)
DD++ さん、すごいですね!!!
てっきりパリティビットが何らかの理由で不要になってしまった 9 ビットの符号なのかと予想
しておりました。全符号の、符号全体のパリティが同一ならば、その 1 ビットは不要となります
ので、それで稼いだのかと……。
まさかの、頭の固い私には無理な発想です。ご教示をありがとうございます。
数珠つなぎの件、中途半端な記述でしたので、精いっぱいきちんと投稿させていただきたく
文を練りました。以下です。
3 ビットのビット列が 7 つあり、それぞれを a, b, c, d, e, f, g と名付けます。この他に、3ビッ
トのビット列が 1 つあり、これを z とします。z = 000 とします。また、
a = 100 、b = 111 、c = 010 、d = 110 、e = 001 、f = 011 、g = 101 とします。
このとき、以下の性質があります。(ここでは、⊕を論理和とします。)
e = a⊕b⊕c 、f = b⊕c⊕d 、g = c⊕d⊕e 、a = d⊕e⊕f 、b = e⊕f⊕g 、c = f⊕g⊕a 、d = g⊕a⊕b
《※サイクリックとなっています。》
3ビットのビット列 x のパリティをここでは p(x) と書くこととします。ビット列の結合を∥で表
します。たとえば、
x = 011, y = 101 のとき、x∥y = 011101 となります。
e, f, g, a, b, c, d, z をエンコードして 10 ビットにしたものをそれぞれ、E, F, G, A, B, C, D,
Z と
名付けます。
さきほどのサイクリックな表をみながら、
E = a∥b∥c∥p(c)
F = b∥c∥d∥p(d)
G = c∥d∥e∥p(e)
A = d∥e∥f∥p(f)
B = e∥f∥g∥p(g)
C = f∥g∥a∥p(a)
D = g∥a∥b∥p(b)
Z = z∥z∥z∥p(z)
とします。具体的には、
E=100∥111∥010∥1 ←e=001
F=111∥010∥110∥0 ←f=011
G=010∥110∥001∥1 ←g=101
A=110∥001∥011∥0 ←a=100
B=001∥011∥101∥0 ←b=111
C=011∥101∥100∥1 ←c=010
D=101∥100∥111∥1 ←d=110
Z=000∥000∥000∥0 ←z=000
となります。このようにサイクリックに作成した符号は、最小ハミング距離が 5 となっています。
これで、不正確なガイガーカウンター報告の数が 0 から 2 までの間ならば、その誤りビット
を訂正可能です。
他にも色々な作り方をしてはみたのですが、一番不思議な踊りを踊っているのが上記のも
のです。なぜうまくいくのかわからないので。タマタマなのかも? しれません。
他の作り方のものも、近々、ご紹介させてください。
kuiperbelt さんからのコメントです。(令和6年9月10日付け)
情報ビットが3ビットでコード長が10ビットのコードで、最小ハミング距離が5のコードであれ
ば、2ビットまでの誤りを検出して訂正することができますが、そのようなコードとして、
0,0,0,0,0,0,0,0,0,0
1,0,0,1,1,0,0,1,1,1
0,1,0,1,0,1,0,1,1,0
1,1,0,0,1,1,0,0,0,1
0,0,1,1,0,0,1,1,0,1
1,0,1,0,1,0,1,0,1,0
0,1,1,0,0,1,1,0,1,1
1,1,1,1,1,1,1,1,0,0
というコードが考えられます。10人の技術者をA~Jとして、
技術者AとEは、1,3,5,7番の金貨を選択して測定、
技術者BとFは、2,3,6,7番の金貨を選択して測定、
技術者CとGは、4,5,6,7番の金貨を選択して測定、
技術者DとHは、1,2,4,7番の金貨を検出して測定、
技術者Iは、1,2,5,6番の金貨を選択して測定、
技術者Jは、1,3,4,6番の金貨を選択して測定することにして、各技術者の陽性の報告を「1」、
陰性の報告を「0」で表すと、
すべての報告が正しかったとすると、以下の8通りの組み合わせがあって、それぞれが
1~8 番のいずれかが偽造品である場合と対応します。
-|A,B,C,D,E,F,G,H,I,J
0|0,0,0,0,0,0,0,0,0,0 →8番が偽造品
1|1,0,0,1,1,0,0,1,1,1 →1番が偽造品
2|0,1,0,1,0,1,0,1,1,0 →2番が偽造品
3|1,1,0,0,1,1,0,0,0,1 →3番が偽造品
4|0,0,1,1,0,0,1,1,0,1 →4番が偽造品
5|1,0,1,0,1,0,1,0,1,0 →5番が偽造品
6|0,1,1,0,0,1,1,0,1,1 →6番が偽造品
7|1,1,1,1,1,1,1,1,0,0 →7番が偽造品
10人の技術者の報告のうち2人の報告が誤りである場合は、10ビットのうち2ビットが誤り
である場合に相当しますが、上記の8状態は最小ハミング距離が5なのでいずれも5ビット
以上の差があり、2ビットの誤り、すなわち、2人の報告が誤りである場合までは訂正するこ
とができます。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年9月11日付け)
技術者が 10 → 21 人に増員されたときに、最大 5人 までの範囲で誤った報告をしてきて
も偽金貨を突き止めることができると判明しました。
"100 111 010 110 001 011 101",
"111 010 110 001 011 101 100",
"010 110 001 011 101 100 111",
"110 001 011 101 100 111 010",
"001 011 101 100 111 010 110",
"011 101 100 111 010 110 001",
"101 100 111 010 110 001 011",
"000 000 000 000 000 000 000",
Minimum Hamming Distance: 12
なお、上記では 21 中に、誤らない技術者が1人報告をロストしても大丈夫です。1人ロスト
かつ2人誤り報告でも。対称性が高いので。
別の言い方をすれば、
技術者が 10 → 20 人に増員されたときに、最大 5人 までの範囲で誤った報告をしてきて
も偽金貨を突き止めることができます。
Minimum Hamming Distance: 11 となりますので。
元の問題からみると、技術者が2倍に増えて、許容できる誤り報告数が2.5倍です。
こんなのをみると、やはり、9人の技術者(うち最大2名は嘘つき)でもできるのでは?と変な
予想をたててしまいたくなります。
kuiperbelt さんからのコメントです。(令和6年9月12日付け)
情報ビットが3ビット、最小ハミング距離が7のコードで、最短なのはコード長が13ビットのコ
ードで、以下のようなものでした。
A,B,C,D,E,F,G,H,I,J,K,L,M
-------------------------
0,0,0,0,0,0,0,0,0,0,0,0,0
1,0,0,1,1,0,1,0,0,1,1,0,1
0,1,0,1,0,1,0,1,0,1,0,1,1
1,1,0,0,1,1,1,1,0,0,1,1,0
0,0,1,0,1,1,0,0,1,0,1,1,1
1,0,1,1,0,1,1,0,1,1,0,1,0
0,1,1,1,1,0,0,1,1,1,1,0,0
1,1,1,0,0,0,1,1,1,0,0,0,1
13人の技術者をA~Mとして、
技術者AとGは、1,3,5,7番の金貨を選択して測定、
技術者BとHは、2,3,6,7番の金貨を選択して測定、
技術者CとIは、4,5,6,7番の金貨を選択して測定、
技術者DとJは、1,2,5,6番の金貨を選択して測定、
技術者EとKは、1,3,4,6番の金貨を選択して測定、
技術者FとLは、2,3,4,5番の金貨を選択して測定、
技術者Mは、1,2,4,7番の金貨を検出して測定
することにすれば、最大で3人までが誤りの報告をしても8枚の金貨から1枚の偽造品を特定
できます。
また、情報ビットが3ビット、最小ハミング距離が9のコードで、最短なのはコード長が17ビッ
トのコードで、以下のようなものでした。
A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q
---------------------------------
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
1,0,0,1,0,0,1,0,0,1,1,1,0,1,1,1,0
0,1,0,0,1,0,0,1,0,1,1,0,1,1,1,0,1
1,1,0,1,1,0,1,1,0,0,0,1,1,0,0,1,1
0,0,1,0,0,1,0,0,1,1,0,1,1,1,0,1,1
1,0,1,1,0,1,1,0,1,0,1,0,1,0,1,0,1
0,1,1,0,1,1,0,1,1,0,1,1,0,0,1,1,0
1,1,1,1,1,1,1,1,1,1,0,0,0,1,0,0,0
17人の技術者をA~Qとして、
技術者AとDとGは、1,3,5,7番の金貨を選択して測定、
技術者BとEとHは、2,3,6,7番の金貨を選択して測定、
技術者CとFとIは、4,5,6,7番の金貨を選択して測定、
技術者JとNは、1,2,4,7番の金貨を検出して測定、
技術者KとOは、1,2,5,6番の金貨を選択して測定、
技術者LとPは、1,3,4,6番の金貨を選択して測定、
技術者MとQは、2,3,4,5番の金貨を選択して測定
することにすれば、最大で4人までが誤りの報告をしても8枚の金貨から1枚の偽造品を特定
できます。
なお、情報ビットが3ビット、最小ハミング距離が3のコードで、最短なのはコード長が6ビット
のコードで、以下のようなものでした。
A,B,C,D,E,F
-----------
0,0,0,0,0,0
1,0,0,1,1,0
0,1,0,1,0,1
1,1,0,0,1,1
0,0,1,0,1,1
1,0,1,1,0,1
0,1,1,1,1,0
1,1,1,0,0,0
6人の技術者をA~Fとして、
技術者Aは、1,3,5,7番の金貨を選択して測定、
技術者Bは、2,3,6,7番の金貨を選択して測定、
技術者Cは、4,5,6,7番の金貨を選択して測定、
技術者Dは、1,2,5,6番の金貨を選択して測定、
技術者Eは、1,3,4,6番の金貨を選択して測定、
技術者Fは、2,3,4,5番の金貨を選択して測定
することにすれば、1人までが誤りの報告をしても8枚の金貨から1枚の偽造品を特定できま
す。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年9月13日付け)
DD++ さんがおっしゃっていた、《10人ではなく9 人、うち2名は《必ず》嘘をつく》場合に解が
あることを、私も確認しました。別解ですね。
9人の技術者を、前半組6人、後半組3人にわけます。
前半では①と②と③とのどれかが発生します。どれが発生したかは我々にはわかります。
後半では、①②③ごとに、対処策があります。
・前半部
8枚の金貨を2枚づつペアにして計4ペアとします。(A,a), (B,b),(C ,c ),(D,d)と名付けます。
あるいは、(X,x)のようにまとめて書くこともあります。
6名の技術者に以下のように測定の指示を出します。1 のマークがついた金貨を測ります。
[
"0 0 0 0 0 0" ,//(A,a)
"0 0 1 1 1 1" ,//(B,b)
"1 1 0 0 1 1" ,//(C,c)
"1 1 1 1 0 0" ,//(D,d)
]
上は、ハミング距離が 4 なので、以下の3つのケースが結果として判明します。
① 陽性判定は偶数個である。が、そのものズバリの判定結果が得られない。
即ち、前半6人組に2人嘘つきがいる。偽物の入った(X,x)はこの時点ではまったく不明。
② 陽性判定は偶数個である、かつ、上の4ケースそれぞれのうちどれかひとつが、そのも
のズバリの結果となる。
このとき、前半6人組に嘘つきがいない。偽物の入った(X,x)が確定する。
③ 陽性判定は奇数個である。が、そのものズバリの判定結果が得られない。
即ち、前半6人組に1人の嘘つきがいる。この場合には嘘つきが特定できて、偽物の入った
(X,x)が確定する。
以上が前半部です。次は、後半部での対処。
① 後半部3名の技術者が正直者なので、8枚の金貨から1枚の偽金貨を見付けるには、
二分木で捜索すればよい。
《目的終了》
② 偽物の入った(X,x)が確定している。残りの3名の技術者のうち2名が嘘つきである。
3名にXが偽造か調べさせ、得られた結果を2対1で多数決をとり、その結果の判定を反
転させたものが真の測定結果となる。
《目的終了》
③ 偽物の入った(X,x)が確定している。残りの3名の技術者のうち1名が嘘つきである。
3名にXが偽造か調べさせ、得られた結果を2対1で多数決をとり、その結果が真の測定
結果となる。
《目的終了》
※以上が別解です.
後半部の多数決が効いてくるためにも、嘘つき2名は必ず嘘をつくことが必要となります。
#なお、揃って嘘をつくとは限らない場合に、9名で足りるかというお話しについては、私は、
かなり否定的に捉えるようになりました。個人的には探索はおわります。
kuiperbelt さんからのコメントです。(令和6年9月13日付け)
技術者を1人増やして11人にすると、偽造品1枚を含む16枚の金貨から、最大2人の誤り
を含む報告を用いて特定することができます。
情報ビットが4ビット、最小ハミング距離が5のコードで、最短なのはコード長が11ビットの以
下のコードで、これを用いると、
-|A,B,C,D,E,F,G,H,I,J,K
-----------------------
0|0,0,0,0,0,0,0,0,0,0,0→16番が偽造品
1|1,0,0,0,1,1,1,0,0,1,0→1番が偽造品
2|0,1,0,0,1,1,0,1,1,0,1→2番が偽造品
3|1,1,0,0,0,0,1,1,1,1,1→3番が偽造品
4|0,0,1,0,1,0,1,1,1,0,0→4番が偽造品
5|1,0,1,0,0,1,0,1,1,1,0→5番が偽造品
6|0,1,1,0,0,1,1,0,0,0,1→6番が偽造品
7|1,1,1,0,1,0,0,0,0,1,1→7番が偽造品
8|0,0,0,1,0,1,1,0,1,1,1→8番が偽造品
9|1,0,0,1,1,0,0,0,1,0,1→9番が偽造品
a|0,1,0,1,1,0,1,1,0,1,0→10番が偽造品
b|1,1,0,1,0,1,0,1,0,0,0→11番が偽造品
c|0,0,1,1,1,1,0,1,0,1,1→12番が偽造品
d|1,0,1,1,0,0,1,1,0,0,1→13番が偽造品
e|0,1,1,1,0,0,0,0,1,1,0→14番が偽造品
f|1,1,1,1,1,1,1,0,1,0,0→15番が偽造品
11人の技術者をA~Kとして、
技術者Aは、1,3,5,7,9,11,13,15番の金貨を選択して測定、
技術者Bは、2,3,6,7,10,11,14,15番の金貨を選択して測定、
技術者Cは、4,5,6,7,12,13,14,15番の金貨を選択して測定、
技術者Dは、8,9,10,11,12,13,14,15番の金貨を選択して測定、
技術者Eは、1,2,4,7,9,10,12,15番の金貨を検出して測定、
技術者Fは、1,2,5,6,8,11,12,15番の金貨を選択して測定、
技術者Gは、1,3,4,6,8,10,13,15番の金貨を選択して測定、
技術者Hは、2,3,4,5,10,11,12,13番の金貨を選択して測定、
技術者Iは、2,3,4,5,8,9,14,15番の金貨を選択して測定、
技術者Jは、1,3,5,7,8,10,12,14番の金貨を選択して測定、
技術者Kは、2,3,6,7,8,9,12,13番の金貨を検出して測定
することにすれば、最大で2人までが誤りの報告をしても16枚の金貨から1枚の偽造品を特
定できます。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年9月14日付け)
kuiperbeltさんによるご投稿へのコメントです。
8 番から 15 番までは本物、という情報があらかじめ与えられていれば、技術者Dによる計
測は不要となり、技術者の総人数は 10 人でよいこととなります。
即ち、0番(=16番)から7番までの8枚の金貨から技術者10名で1枚の偽造金貨をみつける方
法にもなっています。(最大2人まで嘘をつくこととして)
以下は、私の投稿の続きです。別解でして、恐ろしく形が憶えやすいものです。
情報ビットは 3 ビットとします。これを w と記します。w について全てのビットを反転したも
のを W とします。
3 ビット分のデータのパリティ(1ビット)を求める関数を p(・)と書きます。ビット列 x とビット
列 y とを結合する記号を∥とします。
w をエンコードして 10 ビットのビット列を次のように作ります。
w∥w∥p(w)∥w …… ただし、p(w)=0 のとき。
w∥w∥p(w)∥W …… ただし、p(w)=1 のとき。
これが目的を果たします。みつけたときには物凄くビックリしました。なぜコレでうまくいくか
というと、・・・。
3ビットの w を1ビットづつに分解すると、 w=w1∥w2∥w3
さきのエンコードは、
w1∥w2∥w3∥w1∥w2∥w3∥w1+w2+w3∥w2+w3∥w1+w3∥w2+w3
トなっています。
※ただし、加算記号は ビット毎の排他的論理和にて。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年9月15日付け)
このスレッドの趣旨からは脱線中です。上記への個人的な気づきです。
「コレ」でうまく行く? という観察から実験数学的にあれこれやっておりました。
符号語の数が 16 で情報ビットが 4 、検査ビットが 3 、符号長が 7 、最小ハミング距離が 3
ゆえにビット反転誤りを 1 ビットまで訂正可能な、(7,4,3)ハミング符号は、よく知られていて世
の中に実際に応用されている枯れた技術のようです。
これに対抗して!?
符号語の数が 16 で情報ビットが 4 、検査ビットが 10 、符号長が 14 、最小ハミング距離
が 7 ゆえにビット反転誤りを 3 ビットまで訂正可能な、そのような符号をたった今みつけま
した。(車輪の再発明かも?)
情報ビットをそのままに、符号長が 7 から 14 と2倍になるのを生贄にして、ビット反転誤り
への訂正能力を 1 ビットから 3 ビットへと、 3 倍にできるという。
通信路の状況が悪いときにはかなり有効なのでは? と。
"0000 000000 0000",
"0001 001011 0111",
"0011 011110 1100",
"0010 010101 1011",
"0110 110011 0110",
"0111 111000 0001",
"0101 101101 1010",
"0100 100110 1101",
"1100 011110 0011",
"1101 010101 0100",
"1111 000000 1111",
"1110 001011 1000",
"1010 101101 0101",
"1011 100110 0010",
"1001 110011 1001",
"1000 111000 1110",
16ビットめへの追加、末尾に全体へのパリティをつけるのも乙なものですが。
とにかく各ビットを怠けさせない、他のビットと相関させる、そんな作戦が良いのかもしれま
せん。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年9月16日付け)
DD++ さんが提起なさった《技術者が 9 人でも大丈夫?》という問いについて、何度も諦め
ようと努めたのですが、なかなか頭を離れず、もう思い切って、とことん考えてみようと試みま
した。
結果として、もしもひとつの【予想】が正しければ、 9 人の技術者(うち、嘘つきは 0 人から
2 人の可能性がある)でも、8枚中1枚の偽金貨を突き止められそうと考えつきました。
偽金貨をつきとめる段階として、第一段階と第二段階とに分けます。
第二段階では第一段階までの中間結果をみてから測定方法を都度考えることにします。
(なお二段階にわけずに一発でやろうとするならば、技術者は10人必要だろうことはほぼ間
違いないという感触を得ています。)
第一段階では、7人の技術者を使い、第二段階では、2人の技術者を使います。
第一段階終了時点で、既に偽造金貨が確定済みならば第二段階は実行しません。この場
合の発生条件は、7人中嘘つきが1人以下であることです。(必要十分条件)
第一段階終了時点で、7名中嘘つきが2名いたと確定できれば、かつ、8枚中少なくとも4枚
が本物であると確定できれば、残りの4枚について第二段階で正直者のみで構成された2名
の技術者がうち1枚の偽金貨を確定できることでしょう。
第一段階のアルゴリズムになにが必要かをまとめなおします。
以下の3パターンのどれかが必ず発生するものとします。
① 嘘つきがちょうど1人発生したことの検知確定と、同時に一枚の偽金貨の確定。
[第二段階不要]
② 嘘つきがちょうど0人であることの検知確定と、同時に一枚の偽金貨の確定。
[第二段階不要]
③ 嘘つきがちょうど2人であることの検知確定と、同時に、本物の金貨(少なくとも)4枚の確
定。偽金貨は残りもののなかにあると絞れる。
[第二段階では2人の正直者が残りものから偽金貨をつきとめることになりますがそれは十分
に可能であることでしょう。]
上のようなアルゴリズムがみつかれば、10人ならず9人でも偽金貨を確定できることとなり
ます。
①〜③までで、もっとも難解なのが③が発生するケースです。
私は次のようなものをとりあえず考えてみました。
第一段階の設計について。
8枚の硬貨にたいして7名の技術者が以下のリストにあるように測定します。
(1)はガイガーカウンターで測ります。
"0 0 0 0 0 0 0",
"0 0 1 0 1 1 1",
"1 0 0 1 0 1 1",
"1 1 0 0 1 0 1",
"1 1 1 0 0 1 0",
"0 1 1 1 0 0 1",
"1 0 1 1 1 0 0",
"0 1 0 1 1 1 0",
ケース①
7つの測定結果が得られた時、陽性(1)が、奇数個、得られたケースです。
このとき、7名中に嘘つきは必ず1名です。
上のテーブルでは最小ハミング距離が4なので嘘つきも確定し偽金貨も確定します。
第二段階は不要です。
ケース②
7つの測定結果が得られた時、陽性(1)が、偶数個、得られ、かつ、上のテーブルと一致した
ケースです。
このとき、7名中に嘘つきはいません。偽金貨も確定します。
第二段階は不要です。
ケース③
7つの測定結果が得られた時、陽性(1)が、偶数個、得られ、かつ、上のテーブルと【一致し
ない】ケースです。
このとき、7名中の嘘つきは必ず2名です。偽金貨は確定しません。
2名の正直者が待っている第二段階が必要です。
=====
ここで実験的にかなりやり込んでみたのですが (手動)、偽測定値を2個含む7個のデータ
を得られたときに、偽金貨の候補は《いつも》3枚なのです。ということは、第二段階で偽金貨
が確定できることとなります。
以下が私の【予想】です。
偽測定値を2個含む7個のデータを得られたときに、偽金貨の候補は《いつも》3枚です。
============
上記の予想に反例があったり、証明があるようでしたならば、是非とも、ご教示をください。
気になって気になって仕方がありません。ボーンヘッドがあるかもですけれども。皆様、何
卒ご教示を賜りたく、宜しくお願い申し上げます。
※証明の見通しがよくなるかどうかわかりませんが、上記のテーブルは巡回的に作ってあ
ります。
DD++ さんからのコメントです。(令和6年9月16日付け)
なるほど、カークマンの組分け問題の解を利用すれば確かにいけますね。
証明は、陽性報告の人数ごとに場合分けをすれば容易かと思います。
いかがでしょう?
Dengan kesaktian Indukmu さんからのコメントです。(令和6年9月16日付け)
DD++ さん、早速のコメントおよびヒントを有難うございます。
陽性報告の人数で場合分け……ですか……、やってみます。
ご指摘どおり、カークマンでしたね……。自分としては、ファノ平面を使ったつもりでした。
(0のポジション)
Dengan kesaktian Indukmu さんからのコメントです。(令和6年9月17日付け)
陽性報告の数が 6 と 2 とではなんとかなりました。4 では整理がつかずに長い列挙になっ
てしまいます。陰性 3 と読み替えてもうまくいかず。スカッとする証明をご教示願えれば幸い
です。
===
皆様へ。
機械に全数検査をしてもらいましたところ、くだんの予想は真のようです。下記で true を出力
してきました。(JavaScriptによるプログラムです)jslint的には超ヤバいです。申し訳ありません。
function hammingDistance(str1, str2) {
// ハミング距離を計算する関数
let distance = 0;
for (let i = 0; i < str1.length; i++) {
if (str1[i] !== str2[i]) {
distance++;
}
}
return distance;
}
function checkCondition(sequences) {
// 条件を満たすかチェックする関数
for (let i = 0; i < sequences.length; i++) {
const originalSeq = sequences[i];
// 2ビットを反転させるすべての組み合わせ
for (let j = 0; j < originalSeq.length; j++) {
for (let k = j + 1; k < originalSeq.length; k++) {
const newSeq = originalSeq.split('');
newSeq[j] = newSeq[j] === '0' ? '1' : '0';
newSeq[k] = newSeq[k] === '0' ? '1' : '0';
const z = newSeq.join('');
let count = 0;
for (const seq of sequences) {
if (hammingDistance(z, seq) === 2) {
count++;
}
}
// ハミング距離が2であるシーケンスが常に3つでなければfalseを返す
if (count !== 3) {
return false;
}
}
}
}
return true;
}
// 与えられたシーケンス
const sequences = ['0000000', '0010111', '1001011', '1100101', '1110010', '0111001', '1011100', '0101110'];
const result = checkCondition(sequences);
console.log(result); // true or falseが出力される
=====
ところで、この作戦がうまくいくのであるならば、2名の嘘つき技術者が常に嘘の報告をして
くるのであるならば、
8枚中の1枚ではなく、9枚中の1枚の偽金貨を特定できるのですね?
0番から7番の金貨についての処理のつもりで今まではお話ししてきましたが、《0番には2枚
を割り当てる》こととします。
従前の①から③のケースで①には変更なし。②では、変更あり。これは嘘つきなしのケー
スですが、1番コインから7番までのどれかにヒットしなければ、第二段階で、2枚の0番のうち
どちらが偽コインなのかを、2名の嘘つきに判定してもらうこととなります。
③では《偽測定値を2個含む7個のデータを得られたときに、偽金貨の候補は《いつも》3枚
です。》ではなく、0番が候補になるときには4枚が偽金貨の候補となります。
第二段階では、正直者の技術者が2名残っていますので偽金貨の特定は可能です。
【うーん?】
DD++ さんからのコメントです。(令和6年9月18日付け)
注目すべきは、陰性報告をしてきた 3 人が、「測定にかけなかった」方のコインですね。
あとは、カークマンの組分け問題は(多分ファノ平面で考えた場合でも?)、任意の 2 つの組
の間に必ず共通人物が 1 人だけ存在することも注目に値します。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年9月23日付け)
DD++ さん、たびたびのヒントを有難うございます。おかげさまで、偽コイン候補が「3個以下」
であるとは示せました。
しかしながら、丁度3個あるというところまではまだいきついておりません。なにか単純なこ
とを見落としているにちがいありません。もう少しだけ考えてみます。
DD++ さんからのコメントです。(令和6年9月24日付け)
陽性報告数 4 だけど矛盾が含まれている場合の話ですよね?
陰性報告をした 3 人を A, B, C とします。
A が嘘つきだと仮定すると、A が測定にかけていて、B と C が測定にかけていないコイン
は本物候補になります。
さて、そのようなコインは何枚存在するでしょうか?
Dengan kesaktian Indukmu さんからのコメントです。(令和6年9月25日付け)
DD++ さん、おっしゃる通りですね!最大のヒントをまことにありがとうございます!
皆様へ、あとでボチボチと証明のアウトラインを書いていく所存です。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月1日付け)
せっかく DD++ さんにヒントをいただいておりますのに、【丁度3個である】ほうの証明をまだ
書き下せておりません。ポンチ絵については漸く出来上がりましたけれども。申し訳ないこと
です。
先の投稿で、私は【3個以下】の証明なら出来たと申しておりました。今日はこちらのほう
のメモ書きを下記に投稿いたします。
金貨の名前を z, a, b, c, d, e, f, g とします。技術者7名には添え字として 1 から 7 を与え
ます。
ガイガーカウンターによる検査結果を q とします。
q は、7名の技術者による陰性(0)、陽性(1) の結果を示す 𝑞₁, 𝑞₂, 𝑞₃, ... , 𝑞₇ として表します。
いま、偽金貨が a である状況下で、技術者が q の検査結果を返したとします。
また、パリティ検査により、q は a に対してハミング距離が 2 であると判明したものとします。
一般性を失わないようにするために、q や、z, a から g までに使われる添え字である、1 か
ら 7 までについて、{h, k, m, n, p, s, t} = {1, 2, 3, 4, 5, 6, 7} とします。
蛇足ですが、両辺の集合の各要素は一対一対応しますけれども順不同です。以下の記述で
一般性を失わないための約束てす。
また、𝑎₁ のビット反転したものを 𝑎̅₁ などと、オーバーラインで表すこととします。
偽金貨 𝑎 に対する検査結果が 𝑞 として与えられるものとします。2 ビットの反転は、ビット位
置 h, k で発生していることとします。
図示すれば、次の2行の各ビットの上と下とは真理値は等しいです。
𝑎̅ₕ, 𝑎̅ₖ, 𝑎ₘ, 𝑎ₙ, 𝑎ₚ, 𝑎ₛ, 𝑎ₜ
𝑞ₕ, 𝑞ₖ, 𝑞ₘ, 𝑞ₙ, 𝑞ₚ, 𝑞ₛ, 𝑞ₜ
この 𝑞 が 𝑏 をも偽金貨の候補として考えられることしましょう。図示しますと以下の3パターン
のみに分かれます。
◆パターン1
𝑎̅ₕ, 𝑎̅ₖ, 𝑎ₘ, 𝑎ₙ, 𝑎ₚ, 𝑎ₛ, 𝑎ₜ
𝑞ₕ, 𝑞ₖ, 𝑞ₘ, 𝑞ₙ, 𝑞ₚ, 𝑞ₛ, 𝑞ₜ
𝑏̅ₕ, 𝑏̅ₖ, 𝑏ₘ, 𝑏ₙ, 𝑏ₚ, 𝑏ₛ, 𝑏ₜ
◆パターン2
𝑎̅ₕ, 𝑎̅ₖ, 𝑎ₘ, 𝑎ₙ, 𝑎ₚ, 𝑎ₛ, 𝑎ₜ
𝑞ₕ, 𝑞ₖ, 𝑞ₘ, 𝑞ₙ, 𝑞ₚ, 𝑞ₛ, 𝑞ₜ
𝑏ₕ, 𝑏̅ₖ, 𝑏̅ₘ, 𝑏ₙ, 𝑏ₚ, 𝑏ₛ, 𝑏ₜ
◆パターン3
𝑎̅ₕ, 𝑎̅ₖ, 𝑎ₘ, 𝑎ₙ, 𝑎ₚ, 𝑎ₛ, 𝑎ₜ
𝑞ₕ, 𝑞ₖ, 𝑞ₘ, 𝑞ₙ, 𝑞ₚ, 𝑞ₛ, 𝑞ₜ
𝑏ₕ, 𝑏ₖ, 𝑏̅ₘ, 𝑏̅ₙ, 𝑏ₚ, 𝑏ₛ, 𝑏ₜ
分析します。
パターン1では、
a と b とは、ハミング距離が 0 となってしまい、本来あるべきハミング距離が4であることと
矛盾します。パターン1はありえません。
パターン2では
a と b とは、ハミング距離が 2 となってしまい、本来あるべきハミング距離が4であることと
矛盾します。パターン2はありえません。
パターン3では
a と b とは、ハミング距離が 4 となり、本来あるべきハミング距離が4であることと矛盾し
ません。パターン3はありえます。
これらより、パターン3のみが、a と b との間の関係を示しています。
パターン3を再掲します。
𝑎̅ₕ, 𝑎̅ₖ, 𝑎ₘ, 𝑎ₙ, 𝑎ₚ, 𝑎ₛ, 𝑎ₜ
𝑞ₕ, 𝑞ₖ, 𝑞ₘ, 𝑞ₙ, 𝑞ₚ, 𝑞ₛ, 𝑞ₜ
𝑏ₕ, 𝑏ₖ, 𝑏̅ₘ, 𝑏̅ₙ, 𝑏ₚ, 𝑏ₛ, 𝑏ₜ
さて、第三の金貨 c が偽造金貨の候補だとしましょう。ありえるパターンは以下のみです。
𝑎̅ₕ, 𝑎̅ₖ, 𝑎ₘ, 𝑎ₙ, 𝑎ₚ, 𝑎ₛ, 𝑎ₜ
𝑞ₕ, 𝑞ₖ, 𝑞ₘ, 𝑞ₙ, 𝑞ₚ, 𝑞ₛ, 𝑞ₜ
𝑏ₕ, 𝑏ₖ, 𝑏̅ₘ, 𝑏̅ₙ, 𝑏ₚ, 𝑏ₛ, 𝑏ₜ
𝑐ₕ, 𝑐ₖ, 𝑐ₘ, 𝑐ₙ, 𝑐̅ₚ, 𝑐̅ₛ, 𝑐ₜ
a と b との関係は、a と c, b と c との関係にもそのまま通用するからです。
測定結果である q について、a, b, c が偽金貨の候補である場合には、ビット反転の関係
は上に尽きることとなります。
ここで、更に、金貨 d が偽金貨の候補足り得るかと問いを立てます。
h,k,m,n,p,s 以外のふたつの位置で、d は q に対してビット反転していなくてはなりませんが
これは不可能です。
ここまでをまとめれば、測定結果 q が与えられたならば、偽金貨であることがありえるのは、
a,b,c, の3枚までで、4枚以上ではあり得ないことがわかりました。
なお、3枚以下であることを示しただけであって、3枚丁度を示したわけではないことを付記
しておきます。
DD++ さんからのコメントです。(令和6年10月1日付け)
あれ?私はわりと答えそのもののつもりで書いてたんですが……。
陽性報告が 4 人だった場合、
・全員正直
・陽性報告と陰性報告それぞれで 1 人嘘つき
のいずれかですよね?
前者はハミング距離 0 で話は終わっています。
後者の場合、陰性報告者のうち 2 人が測定から外したコインが本物候補です。そして、そ
れは任意の陰性報告者 2 人組の間に共通で測定しなかったコインが(誰も測らなかったや
つ以外で)必ずちょうど 1 枚あり、合計で 3C2 = 3 枚存在します。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月4日付け)
DD++ さん、たびたびお手を煩わせてしまいまして申し訳ございませんでした。有難うござ
います。
■問題の振り返りをします。
このページ冒頭の問題では、10 人のケースでは解あり、では、9人では? となったのがこ
との発端です。
9人のうち、第一段階で7人を投入、そこで偽金貨が特定できればよし、そのなかに虚偽の
レポートをしてくる技術者が2人いるケースもありうるが、その場合には偽金貨が特定できな
いものの、偽金貨の候補が【丁度】3枚になるので、第二段階として残りの正直な技術者2名
が偽金貨を特定できるだろう、ゆえに技術者は、9人で十分だ、という筋書きなのでした。
今回は、第一段階のアルゴリズムを決定し、なおかつ【丁度3人】問題について、個人的
な結論を皆さんにご報告いたします。
///////////
ご注意:ここまでの流れと陰性陽性の扱いが逆転してしまっています。申し訳ありません。
(ひとえに私の直観にあわせてしまっただけなのですが……)
///////////
■第一段階での測定について
i を 1 から 7 までの添字として使います。j を 1 から 8 までの添字として使います。
7人いる技術者に、1 から 7 と名前をつけます。添字としてはもっぱら i を使います。
陽性集合 Pj を以下のように定義します。
P1 = {2, 3, 5}
P2 = {3, 4, 6}
P3 = {4, 5, 7}
P4 = {5, 6, 1}
P5 = {6, 7, 2}
P6 = {7, 1, 3}
P7 = {1, 2, 4}
P8 = {1, 2, 3, 4, 5, 6, 7}
※余談ですが P1 から P7 は、FANO平面となっています。P8 は余計ものです。
陰性集合 Nj を以下のように定義します。
N1 = {7, 6, 4, 1}
N2 = {1, 7, 5, 2}
N3 = {2, 1, 6, 3}
N4 = {3, 2, 7, 4}
N5 = {4, 3, 1, 5}
N6 = {5, 4, 2, 6}
N7 = {6, 5, 3, 7}
N8 = { }
8 枚の金貨に以下のように名前をつけます。
C{Pj, Nj}
すなわち、金貨の名前については陽性集合と陰性集合の組みの集合で定義します。
■第一段階での測定について
7人の技術者に次のように測定の指示をだします。すなわち、i 番目の技術者は、Pj の要素
に i を含むような金貨 C{Pj, Nj} をガイガーカウンターで計測します。
◆早見表 | 1 2 3 4 5 6 7 ←技術者
C{P1, N1} | 0 1 1 0 1 0 0
C{P2, N2} | 0 0 1 1 0 1 0
C{P3, N3} | 0 0 0 1 1 0 1
C{P4, N4} | 1 0 0 0 1 1 0
C{P5, N5} | 0 1 0 0 0 1 1
C{P6, N6} | 1 0 1 0 0 0 1
C{P7, N7} | 1 1 0 1 0 0 0
C{P8, N8} | 1 1 1 1 1 1 1
※この早見表では、1 が立っている金貨を計測します。
陽性のレポートをした技術者の集合を T と名づけます。
Tから偽金貨のゆくえを探すということとなります。たとえば、T={2,3,5} ならば偽金貨は
C{P1, N1} ということとなります。
■計測結果Tの評価について
簡単なものから順に。
① T = Pj となる j があるとき
※7人ともに正しいレポートを提出したこととなります。偽金貨は、C{Pj, Nj}。
②Tの要素数が 2 のとき
※すなわち陽性を陰性と偽ったレポートがひとつあったことになります。
j = 8 を除外できます。Pj ⊃ T なる j が唯一に定まります。偽金貨は、C{Pj, Nj}。
③Tの要素数が 4 のとき
※陰性を陽性と偽ったレポートがひとつあったことになります。
j = 8 を除外できます。Pj ⊂ T なる j が唯一に定まります。偽金貨は、C{Pj, Nj}。
④Tの要素数が 6 のとき
※陰性を陽性と偽ったレポートがひとつあったことになります。偽金貨は、C{P8, N8}。
ここまで、①②③④は、T と偽金貨の Pj とのハミング距離が 0 または 1 なのでした。
⑤Tの要素数が 1 のとき
※陽性を陰性と偽ったレポートがふたつあったことになります。j = 8 を除外できます。
このとき T の要素を信じることができます。誤ったふたつのレポートの影響を受けていない
ためです。T ⊂ Pj となる j は3つあります。(FANO平面の性質です)
3つある偽金貨の候補 C{Pj, Nj} については第二段階で、(これ以上は誤ったレポートが発生
しないため) 処理可能となります。
⑥Tの要素数が 5 のとき、偽金貨の候補としてふたつのグループが考えられます。
⑥‐1
※C{P8, N8} について、陽性を陰性と誤ったレポートが2通発生したケースです。
偽金貨の候補として、これがひとつめのグループです。
⑥‐2
※j=8 を除外しての C{Pj, Nj} について、陰性を陽性と誤ったレポートが2通発生したケース
です。
誤ったレポートを出した技術者の添字の値を m,n とします。
{m} ⊂ Pj なる C{Pj, Nj} は 3個あります。これは FANO平面の性質です。
{n} ⊂ Pj なる C{Pj, Nj} は 3個あります。これも FANO平面の性質です。
{m,n} ⊂ Pj なる C{Pj, Nj} は 1個あります。これは FANO平面の性質です。
誤ったレポート m,n を含んだC{Pj, Nj}は、3+3-1=5 より、5個あります。
j=8 を除外しての C{Pj, Nj} の7個のうち、本物の金貨として除外できるのは5個となり、偽
金貨の候補は2個となります。
やや迂遠な論法でしたが、T ⊃ Pj を満たす j は2つあるということとなります。
⑥‐3
以上より、この⑥のケースでは、偽金貨の候補の枚数は3枚となりました。
(つづきます。次は私にとっての天王山で、DD++ さんからお知恵を拝借した部分です。)
DD++ さんからのコメントです。(令和6年10月4日付け)
私にとっても直観と逆でしたので、この変更はありがたいです。6-2 は、陽性を陰性と偽っ
た報告がない以上、陰性報告は全て信じてよく、それで 5 枚が本物と確定できますね。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月4日付け)
DD++ さんのコメントを見て、あっと叫びました。それはそうですね……自明なものを私のよ
うにこねくりまわしてはダメですね……。気を取り直して。以下では、A∖B を差集合の表記と
します。
⑦Tの要素数が 3 のとき(ただし、①のケースは除きます。)
※陽性を陰性にする誤ったレポート1通と、陰性を陽性にする誤ったレポートを1通と、計2本
の誤ったレポートが発生しているケースです。
話の都合上、T に基づいてUを作ります。Uが全体集合でなくてすみません。
U = {1, 2, 3, 4, 5, 6, 7}∖T
そして、偽金貨のC{Pj, Nj}について
Pj = {x, y, z} 、Nj = {p, q, r, s}
とします。
T = {p, y, z,} 、U = {x, q, r, s}
が測定の結果として得られていることとなります。
Tの3つの要素のうち、偽レポートがひとつあるので、その可能性は丁度3通りあります。
偽物を大文字で書くと、
Pj = {X, y, z} 、Pj = {x, Y, z} 、Pj = {x, y, Z}
のどれかが実現していることとなります。
Tに含まれる3つの要素のうち2つを選ぶと、それぞれに対応して金貨がひとつ定まるとい
うこととなります。
以上より、この⑦のケースでは、偽金貨の候補の枚数は3枚となりました。
さて、結論です。以上をまとめますと、第一段階で7人中に2人分の偽レポートが発生した
ときには、偽金貨候補は常に3個であることがわかります。誤りレポートの数が 0 ないし 1
であるときには、偽金貨は確定します。
《感想》 もうちょっと簡単に書ければ良いのですが...。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月7日付け)
上記に提示させていただいた早見表で、再び、0 と 1 とをビットフリップした上で、下記に
再掲させていただきます。
C{P1, N1} | 1 0 0 1 0 1 1 //C4
C{P2, N2} | 1 1 0 0 1 0 1 //C6
C{P3, N3} | 1 1 1 0 0 1 0 //C7
C{P4, N4} | 0 1 1 1 0 0 1 //C3
C{P5, N5} | 1 0 1 1 1 0 0 //C5
C{P6, N6} | 0 1 0 1 1 1 0 //C2
C{P7, N7} | 0 0 1 0 1 1 1 //C1
C{P8, N8} | 0 0 0 0 0 0 0 //C0
なお、各行の右端は、これから始める説明の都合上、各金貨に新しく名前づけしたものです。
ビット列の排他的論理和の記号として「⊕」を使うこととします。
たとえば、 0110 ⊕ 1010 = 1100 です。
1 ≤ n ≤7 について、C0 ⊕ Cn = Cn は、自明ですね。
ビックリしたのが、以下のようになっていることです。
C3 = C2 ⊕ C1
C5 = C4 ⊕ C1
C6 = C4 ⊕ C2
C7 = C4 ⊕ C2 ⊕ C1
つまり、C1、C2、C4 さえ知っていれば、他については、2進数の仕掛けによって割り出せる
ということになります。
これは私にとっては非自明なことですので、皆様にもご報告する次第です。
OEIS の「A075931」:
List of codewords in binary lexicode with Hamming distance 5 written as decimal numbers.
から、
0,31,227,252,805,826,966,985,1354,1365,1449,1462,1647,1648,1676,1683
までを利用して、符号長 11 、最小ハミング距離 5 の符号のビット列を以下のように作成し
ました。
"12 0 3 00 4 0000"←↓見出し
"00 0 0 00 0 0000",//0
"00 0 0 00 1 1111",//1
"00 0 1 11 0 0011",//2
"00 0 1 11 1 1100",//
"01 1 0 01 0 0101",//4
"01 1 0 01 1 1010",
"01 1 1 10 0 0110",
"01 1 1 10 1 1001",
"10 1 0 10 0 1010",//8
"10 1 0 10 1 0101",
"10 1 1 01 0 1001",
"10 1 1 01 1 0110",
"11 0 0 11 0 1111",
"11 0 0 11 1 0000",
"11 0 1 00 0 1100",
"11 0 1 00 1 0011",
見出しについて説明します。
"12 0 3 00 4 0000"
で、1,2,3,4 は、データビット(4ビット)として使えるビット位置です。上位から昇順にしています。
"12 0 3 00 4 0000"
"01 1 0 01 1 1010",
上の例では、0101 を意味しており、10進では 5 です。これが、確かに 0 オリジンで 5 番目
のビット列であることに留意して頂ければ幸いです。
上の一覧表は、4ビットのデータビットの符号語を、11ビットにエンコードしたものとなってい
ます。
前回の投稿で発生していた摩訶不思議な現象が、上でもおきているのかについてプログラ
ムで検証しましたところ、オーケーとなりました。
"00 0 0 00 1 1111",//1
"00 0 1 11 0 0011",//2
"01 1 0 01 0 0101",//4
"10 1 0 10 0 1010",//8
を知っていれば、他の11個の符号語は、排他的論理和でもって計算できるのです。
いや、これ自明だろうとお感じになられるかたもいらっしゃるかもしれません。
しかしながらですね、この「A075931」の数列は、0 から順に 1 づつ カウントアップしていき、
テーブル上にためてある(先行する)全ての数とハミング距離が5以上となる数をみつけてはテ
ーブルに追加して溜め込んでいるだけで、作っているんです。貪欲アルゴリズムでもってグリ
ーディに。有る意味では汚い作り方。
なのに、前回の投稿で触れた法則がある、そもそも、「A075931」で、私が勝手に設定した
【見出し】が、符号語の値を直に示しているなんて、不思議で不思議でならないのです。
たとえば、最小ハミング距離が 6 で、符号長が 13 、符号語数も 13 の、次の符号には、
今話題にしている[法則]を私はみつけられません。
"0011101111101",
"1001110111110",
"0100111011111",
"1010011101111",
"1101001110111",
"1110100111011",
"1111010011101",
"1111101001110",
"0111110100111",
"1011111010011",
"1101111101001",
"1110111110100",
"0111011111010",
データビットがどこなのかも曖昧ですしね。サイクリックですから。
綺麗な仕掛けで作った割には、グリーディに作ったものに、有る意味、負けているのです。
この謎、面白くてしょうがないです。
上記で、私は無手勝流にデータビットの位置を決めていたのですが、(つまりチェックビットの
位置を決めていたのですが)、とっくの昔にコンウェイさんが決めて?ました。どうやったんやろ?
このテーブルが大きくなると、これらの位置はさしかわるとのこと。まあ...。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月11日付け)
13枚の金貨があり、そのうち1枚は放射性物質を含む偽物です。この偽物をガイガーカウン
ターを用いた一連の測定で特定する課題です。問題は以下のように構成されています:
金貨:13枚の金貨があり、1から13まで番号が振られています。ちょうど1枚が偽物です。
偽物の特性:偽の金貨は放射性物質を含んでおり、ガイガーカウンターで検出可能です。
技術者:13人の技術者が測定を行います。
測定プロセス:
各技術者は13枚の金貨のうち一部を選んで測定します。技術者は選ばれた金貨をガイガ
ーカウンターで同時に検査します。ガイガーカウンターは、選ばれた金貨の中に偽物が含ま
れている場合にのみ反応します。測定結果は、その技術者のみが知っています。
測定の制約:各技術者は正確に1回だけ測定を行い、合計13回の測定が行われます。
報告:各測定の後、技術者は「陽性」(放射線が検出された)または「陰性」(放射線が検出さ
れなかった)と報告します。
信頼性の問題:技術者のうち最大2人までが、意図的な欺瞞や偶発的な誤りにより不正確な
報告をする可能性があります。
目標:最大2件の不正確な報告があったとしても、偽の金貨を確実に特定することが目標です。
♦課題♦
この制約と技術者の報告における不正確さを考慮しながら、偽の金貨を確実に特定できる
測定戦略と解析アルゴリズムを設計することが課題です。
技術者に名前A、2、3、4、5、6、7、8、9、X、J、Q、Kを割り当てます。13枚の金貨を次のよ
うに名前付けします:
C_{A, 2, 6, Q}
C_{2, 3, 7, K}
C_{3, 4, 8, A}
C_{4, 5, 9, 2}
C_{5, 6, X, 3}
C_{6, 7, J, 4}
C_{7, 8, Q, 5}
C_{8, 9, K, 6}
C_{9, X, A, 7}
C_{X, J, 2, 8}
C_{J, Q, 3, 9}
C_{Q, K, 4, X}
C_{K, A, 5, J}
特性
1. 数学の概念である集合を用いて金貨の名前をインデックス付けしています。
例えば、C_{K, A, 5, J}とC_{A, 5, K, J}は同じ金貨を指します。
2. 各技術者は、インデックスに自分の名前を含む4枚の金貨を独立して測定します。
3. 各金貨はちょうど4人の技術者によって測定されます。
測定プロセス
Tを、割り当てられた金貨について陽性結果を報告した技術者の集合とします。
Tの例
T = {A, 3, 4, 8, J, K}
T = {2, 4, 9, X, K}
T = {2, 8, X, Q}
T = {6, 8, 9}
T = {J, 9}
⬛⬜⬛⬜⬛⬜
上記の計測方法でうまくいくのだと、ハミング距離という概念の説明ぬきに、集合概念を知っ
ている小学生に教えるにはどうしたらよいでしょうか?
計測の結果として得られた集合 T の要素となったおのおのの技術者が計測した4枚のコ
インに、技術者ごとに、偽物ポイントを 1 づつ与えます。
たとえば、T の要素に 2(技術者の名)があれば、
C_{A, 2, 6, Q}
C_{2, 3, 7, K}
C_{4, 5, 9, 2}
C_{X, J, 2, 8}
の4枚に偽物ポイントを 1 づつ付与します。
13 人の技術者のうち、放射線陽性の報告をあげた技術者の全てについて上記の操作を
おこなった結果として、偽物ポイントが最大のものがユニークに定まります。それが偽金貨
です。
⬛⬜⬛⬜⬛⬜
これがなぜうまくいくのか?という疑問です。小学生にもわかる説明はありますでしょうか?
申し遅れました。早見表は以下の通りです。
'A23456789XJQK'
'1100010000010', //C_{A, 2, 6, Q}
'0110001000001', //C_{2, 3, 7, K}
'1011000100000', //C_{3, 4, 8, A}
'0101100010000', //C_{4, 5, 9, 2}
'0010110001000', //C_{5, 6, X, 3}
'0001011000100', //C_{6, 7, J, 4}
'0000101100010', //C_{7, 8, Q, 5}
'0000010110001', //C_{8, 9, K, 6}
'1000001011000', //C_{9, X, A, 7}
'0100000101100', //C_{X, J, 2, 8}
'0010000010110', //C_{J, Q, 3, 9}
'0001000001011', //C_{Q, K, 4, X}
'1000100000101', //C_{K, A, 5, J}
最小ハミング距離は 6 となっています。
りらひいさんからのコメントです。(令和6年10月13日付け)
ハミング距離をよく知らない私が説明にトライ。理論はわかってないので、こうすれば説明
できるんじゃないかなと思うことを書いてみる。全部のパターンをやってみて大丈夫だねとい
う、ごり押し説明なので長いです。
金貨の名前が長いので、上から順に "あ","い",…,"す" としましょう。もとの金貨の名前か
ら、今度はそれぞれの技術者が測定する金貨の名前の集合を作ります。ちょっと大変です
が、頑張れば次のようになります。
A:{あ,う,け,す}
2:{あ,い,え,こ}
3:{い,う,お,さ}
4:{う,え,か,し}
5:{え,お,き,す}
6:{あ,お,か,く}
7:{い,か,き,け}
8:{う,き,く,こ}
9:{え,く,け,さ}
X:{お,け,こ,し}
J:{か,こ,さ,す}
Q:{あ,き,さ,し}
K:{い,く,し,す}
ここで、たとえば、金貨"い"を測定する技術者を集めてみます。
2:{あ,い,え,こ}
3:{い,う,お,さ}
7:{い,か,き,け}
K:{い,く,し,す}
すると、"い"以外の12枚の金貨は、どれも、この4人の技術者(2,3,7,K)のなかのだれか1人
だけが測定していることがわかります。
同様に、ほかの金貨を測定する4人の技術者を見てみても、残り12枚の金貨を4人のなか
のだれか一人だけが測定するようになっています。
気になったら、あとでそれぞれの金貨で確認してみてください。このことがこの方法でうまく
いく最大の理由です。
さて、まずは技術者全員が正確な報告をした場合を考えましょう。
この場合、4人が陽性(自分が測定した4枚中に偽物あり)と報告し、残り9人が陰性(自分が
測定した4枚中に偽物なし)と報告することになります。
たとえば、金貨"い"が偽物だった場合、技術者{2,3,7,K}が陽性報告、他の技術者が陰性報
告となります。
このとき、金貨"い"の偽物ポイントが4になり、残りの金貨の偽物ポイントは1になります。
なぜなら、先ほど確認したように、金貨"い"を測定する4人の技術者は、"い"以外の12枚
の金貨を重複することなくだれか1人だけが測定しているからです。
別の金貨が偽物だった場合でも同様に、偽物が4ポイント、その他の金貨が1ポイントにな
ります。
よって、技術者全員が正確な報告をした場合は偽物を見分けられることがわかりました。
次に、不正確な報告をした技術者がいた場合を考えます。
これは次のように5パターンが考えられます。
・偽物を測定した4人のうちの1人が陽性(偽物あり)ではなく陰性(偽物なし)と報告した場合。
・偽物を測定した4人のうちの2人が陽性(偽物あり)ではなく陰性(偽物なし)と報告した場合。
・偽物を測定しなかった9人のうちの1人が陰性(偽物なし)ではなく陽性(偽物あり)と報告した
場合。
・偽物を測定しなかった9人のうちの2人が陰性(偽物なし)ではなく陽性(偽物あり)と報告した
場合。
・偽物を測定した4人のうちの1人が陽性(偽物あり)ではなく陰性(偽物なし)と報告し、かつ、
偽物を測定しなかった9人のうちの1人が陰性(偽物なし)ではなく陽性(偽物あり)と報告した
場合。
順番に見ていきましょう。
偽物を測定した4人のうちの1人が陽性(偽物あり)ではなく陰性(偽物なし)と報告した場合は、
不正確な報告をした人が測定していた金貨の偽物ポイントが1ポイント減るので、偽物金貨が
3ポイント、その他の金貨は1ポイントまたは0ポイントになります。
よって偽物を見分けられます。
偽物を測定した4人のうちの2人が陽性(偽物あり)ではなく陰性(偽物なし)と報告した場合
は、不正確な報告をした人が共通して測定していた偽物のポイントが2ポイント減り、不正確
な報告をした人が測定していた他の金貨のポイントは1ポイント減るので、偽物金貨が2ポイ
ント、その他の金貨は1ポイントまたは0ポイントになり、偽物を見分けられます。
偽物を測定しなかった9人のうちの1人が陰性(偽物なし)ではなく陽性(偽物あり)と報告した
場合は、不正確な報告をした人が測定していた金貨の偽物ポイントが1ポイント足されること
になります。不正確な報告をした人が測定したのは偽物でない金貨なので、偽物金貨は4ポ
イント、その他の金貨は1ポイントまたは2ポイントになります。よって偽物を見分けられます。
偽物を測定しなかった9人のうちの2人が陰性(偽物なし)ではなく陽性(偽物あり)と報告した
場合は、不正確な報告をした人2人が共通して測定していた金貨は2ポイント追加され、不正
確な報告をした人のうちどちらか1人だけが測定していた金貨は1ポイントが追加されるので、
偽物金貨は4ポイント、その他の金貨は1ポイントまたは2ポイントまたは3ポイントになり、偽
物を見分けられます。
最後に、偽物を測定した4人のうちの1人が陽性(偽物あり)ではなく陰性(偽物なし)と報告し、
偽物を測定しなかった9人のうちの1人が陰性(偽物なし)ではなく陽性(偽物あり)と報告した場
合を考えます。陽性を陰性と報告した人が測定した金貨は1ポイント減少し、陰性を陽性と報
告した人が測定した金貨は1ポイント増加します。これにより、偽物金貨は3ポイント、その他
の金貨は1ポイントまたは0ポイントまたは2ポイントになるので、偽物を見分けられます。
以上により、不正確な報告を行った技術者が最大2人いたとしても、偽物を特定できること
がわかります。
さて、小学生には難解すぎる説明になってしまったうえに、これがなぜうまくいくのか?の
「なぜ」の部分にちゃんと答えられていないことから、Dengan kesaktian Indukmu さんの質問
に答えたとはいえないでしょうね……。すみません。
DD++ さんからのコメントです。(令和6年10月13日付け)
りらひいさんは、「誰がどんなタイプの嘘をついたか事前にわかっている前提」で書いている
ような?Dengan kesaktian Indukmu さんは、「誰がどんなタイプの嘘をついたかわかっていな
い前提」での話を尋ねているのではないかと思います。
説明はこんな感じでしょうか?
仮に全員が正直に報告した場合、本物は偽物ポイント1、偽物は偽物ポイント4になります。
ここで、研究者の誰かが嘘をついたとします。
もし、陽性を報告するはずの研究者が誤って陰性と報告した場合、該当する4枚の偽物ポ
イントが誤って1下がります。逆に、もし、陰性を報告するはずの研究者が誤って陽性と報告
した場合、該当する4枚の偽物ポイントが誤って1上がります。
すなわち、研究者が1人報告を誤るごとに、2枚のコインの偽物ポイントの差が誤って1変化
する可能性があります。
……が、本物と偽物の偽物ポイント差は本来3ポイントあるので、誤りが2人までならその大
小関係が逆転することはありません。
したがって、どんな場合でも偽物ポイントが最大であるものが偽物で確定です。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月13日付け)
りらひいさん、DD++ さん、まことに有難うございました。おかげさまでスッキリいたしました。
容疑ポイントで逆転がおきえないことをスマートに説明することができるようになりました。
残り12枚の金貨を4人のなかのだれか一人だけが測定するようになっています。
の視点も重要と存じます。というのは、追加で14枚めのコインがあったとして、全技術者が
必ずこのコインを計測する、その他のコインについてはここまでの従前通り、としても、最小
ハミング距離は 6 のままですので、やはり偽コインの特定は成功することとなります。
でも、この場合に今回の仕様の容疑者ポイントを使った方法では、なんだかとてもめんど
くさいことになります。別の手が欲しいところですが、なかなかです。
DD++ さんからのコメントです。(令和6年10月13日付け)
考え直して、りらひいさんに誤った指摘をしてしまっていたことに気づきました。
証明はどんな嘘が混ざったかを前提にしてますが、最終的に判断する方法は「偽物ポイント
が最大のもの」で共通しているので、嘘の混ざり方がわからないまま実行してOKな手順なん
ですねコレ。失礼しました。
りらひいさんからのコメントです。(令和6年10月13日付け)
DD++さん、わたしも言葉が足りていなかったと反省しています。
技術者全員が正確な報告をした場合について書き始める前に、
「不正確な報告がどのような場合であっても偽物を特定できることを示すために、不正確な報
告を分類してすべての場合で偽物を判別できるかを個別に考える。」
みたいな一文があればよかったのでしょう。
それから、「さて、まずは…」という書き始めも誤解を生んだ可能性がありますね。言葉の選
び方が悪かった面もあると思います。
DD++さんのお言葉から判断するに、
偽物の判断基準を私の投稿内で明示しなかったこともよくなかったみたいですね。偽物の
判断基準は、Dengan kesaktian Indukmu さんの投稿に示されていて、共通認識になっている
と思い端折ってしまいました。すみませんでした。
さて、私が投稿した説明についてもう少し反省を……。
まず、後半の場合分け自体が過剰な回答でしたね。DD++ さんの説明が簡潔でわかりやす
いと思います。
そして、前半の集合の再構築も特に不要でした。
「ある1つの金貨を測定する4人の技術者を集めたとき、残り12枚の金貨はそれぞれこの4
人のなかのだれか一人だけが測定する」
ということを示すには、各技術者が測定する金貨の名前の集合を作った方がわかりやすいと
思ったのですが、もとのDengan kesaktian Indukmu が書かれた金貨の名前のリストだけで十
分に確認可能でした。
その説明は次のような感じです。
***
C_{2, 3, 7, K}を測定する4人の技術者2,3,7,Kが測定するほかの金貨について考える。
C_{2, 3, 7, K}以外の金貨の名前を見てみると、どれも2,3,7,Kのなかのどれか一つだけを含
むことがわかる。これは、C_{2, 3, 7, K}以外の12枚の金貨をこの4人のなかのだれか一人だ
けが測定することを意味する。ほかの金貨の場合でも同様のことが成り立つ。
***
こんな感じの説明でいけました。金貨に名前を付けなおして集合を作るくだりはいらなかっ
たですね。
やっぱり思いついたことをそのまま書き連ねた後に大して推敲せずすぐに投稿すると、後々
直した方がいい箇所がいろいろ見つかりますね。
kuiperbelt さんからのコメントです。(令和6年10月14日付け)
小学生向けの説明ではありませんが、13枚の金貨への13人の技術者の割り当ては、以下
のように、GF(3)上の射影平面の9点に9人の技術者が対応し、残りの4人がGF(3)上の射影平
面の無限遠点に対応しますね。
A:(0,0,1) 2:(1,0,1) Q:(2,0,1)
5:(0,1,1) 3:(1,1,1) X:(2,1,1)
J:(0,2,1) 7:(1,2,1) 4:(2,2,1)
6:(1,0,0),K:(0,1,0),8:(1,1,0),9:(2,1,0)は、直線A-2-Q,A-5-J,A-3-4,A-7-Xの延長上の無限遠点
に対応します。
GF(3)上の射影平面の直線は、
A-2-Q-6,5-3-X-6,J-7-4-6,
A-5-J-K,2-3-7-K,Q-X-4-K,
A-3-4-8,2-X-J-8,Q-5-7-8,
A-7-X-9,5-2-4-9,J-3-Q-9,
6-8-K-9
の13本ですが、13本の直線がそれぞれ13枚の金貨に相当します。
13人の技術者が全て真の報告をするのであれば、偽金貨が1枚のときは4人が陽性、9人
が陰性の報告をすることになります。
13人の技術者のうち、最大2人が偽の報告をする場合、偽の報告を偽陽性、偽陰性とする
と、13人からの報告は、
①3人が陽性、1人が偽陰性、9人が陰性
②2人が陽性、2人が偽陰性、9人が陰性
③4人が陽性、1人が偽陽性、8人が陰性
④4人が陽性、2人が偽陽性、7人が陰性
⑤3人が陽性、1人が偽陰性、1人が偽陽性、8人が陰性
となります。
①②の場合、
GF(3)上の射影平面上の直線は、2点が特定されると一意に決まるので、偽金貨を特定する
ことができます。
③④の場合、
GF(3)上の射影平面上の直線には4点が含まれ、陽性の報告をした技術者は同一直線上の
4点に相当し、偽陽性の報告をした技術者は、当該直線外の点に相当します。偽陽性の報告
をした技術者が2人までなので、直線外の点は2個しかなく、偽金貨に相当する直線以外に4
点が並ぶことがないので偽金貨を特定することができます。
⑤の場合、
陽性の報告をした技術者は同一直線上の3点に相当し、偽陽性の報告をした技術者は、当
該直線外の1点に相当します。偽金貨に相当する直線上の3点のうち2点と当該直線外の1点
を同時に通る直線というのは存在しないので、偽陽性を報告した技術者に相当する点を結ぶ
直線上には、陽性あるいは偽陽性を報告した技術者に相当する点が2点しか存在しないこと
になります。こうして、陽性あるいは偽陽性の報告した技術者に相当する点のうち3点が並ぶ
直線に相当する金貨が偽金貨と特定されます。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月14日付け)
はい。PG(2,3)および同じ構造ですが(2,3) Singerは以下の特徴を共有します:
点の数: 13点
直線の数: 13直線
各直線上の点の数: 4点
各点を通る直線の数: 4直線
kuiperbelt さんからのコメントです。(令和6年10月15日付け)
13個の金貨13人の技術者の場合は、GF(3)上の射影平面を応用していましたが、15個の
金貨15人の技術者の場合は、GF(2)上の3次元射影空間を応用して、15人の技術者に1~9、
A~Fの名前をつけて、15個の金貨に、「あ」~「そ」の名前をつけて、それぞれの金貨を以下
のように7人の技術者が測定することにします。
あ:1,2,3,4,9,A,B
い:1,2,5,6,9,C,D
う:1,3,5,7,A,C,E
え:5,6,7,8,9,A,B
お:3,4,7,8,9,C,D
か:2,4,6,8,A,C,E
き:1,3,6,8,A,D,F
く:1,2,7,8,9,E,F
け:1,4,5,8,B,C,F
こ:9,A,B,C,D,E,F
さ:1,4,6,7,B,D,E
し:3,4,5,6,9,E,F
す:2,4,5,7,A,D,F
せ:2,3,6,7,B,C,F
そ:2,3,5,8,B,D,E
1~9、A~Fの技術者に、GF(2)上の3次元射影空間内の点を以下のように対応させると、
「あ」~「そ」の金貨は、GF(2)上の3次元射影空間内の平面に対応します。
1:(0,0,0,1) 2:(1,0,0,1) 3:(0,1,0,1) 4:(1,1,0,1)
5:(0,0,1,1) 6:(1,0,1,1) 7:(0,1,1,1) 8:(1,1,1,1)
9:(1,0,0,0) A:(0,1,0,0) B:(1,1,0,0)
C:(0,0,1,0) D:(1,0,1,0) E:(0,1,1,0) F:(1,1,1,0)
全員が真の報告をした場合、偽金貨の偽物ポイントは7で本物の金貨の偽物ポイントは3
となります。
陽性を報告するはずの技術者が陰性と報告した場合、該当する7枚の偽物ポイントが1下
がります。
陰性を報告するはずの技術者が陽性と報告した場合、該当する7枚の偽物ポイントが1上
がります。
したがって、技術者が1人報告を偽るごとに、偽物ポイントの差が1だけ減少します。しかし、
本物と偽物の偽物ポイントの差は本来4ポイントあるので、偽りの報告が3人までならその大
小関係が逆転することはありません。
対応する15ビット符号の最小ハミング距離は8になるので、偽りの報告が3人までなら偽金
貨を特定することができますが、偽りの報告が4人になると報告に偽りがあることはわかっ
ても、偽金貨を特定することはできなくなります。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月15日付け)
なるほど、これは勉強になりました。サイクリックに翻訳できましたのでお礼に。
[
"0,1,1,1,0,0,0,0,1,0,1,0,0,1,1",
"1,0,1,1,1,0,0,0,0,1,0,1,0,0,1",
"1,1,0,1,1,1,0,0,0,0,1,0,1,0,0",
"0,1,1,0,1,1,1,0,0,0,0,1,0,1,0",
"0,0,1,1,0,1,1,1,0,0,0,0,1,0,1",
"1,0,0,1,1,0,1,1,1,0,0,0,0,1,0",
"0,1,0,0,1,1,0,1,1,1,0,0,0,0,1",
"1,0,1,0,0,1,1,0,1,1,1,0,0,0,0",
"0,1,0,1,0,0,1,1,0,1,1,1,0,0,0",
"0,0,1,0,1,0,0,1,1,0,1,1,1,0,0",
"0,0,0,1,0,1,0,0,1,1,0,1,1,1,0",
"0,0,0,0,1,0,1,0,0,1,1,0,1,1,1",
"1,0,0,0,0,1,0,1,0,0,1,1,0,1,1",
"1,1,0,0,0,0,1,0,1,0,0,1,1,0,1",
"1,1,1,0,0,0,0,1,0,1,0,0,1,1,0",
];
GAI さんからのコメントです。(令和6年10月17日付け)
Dengan kesaktian Indukmu さんの投稿行列をみて、例えば、次のような 31×31 のものが
構成できれば、31個の金貨と31人の検査官で15個ずつの硬貨を調査していき、問題の硬
貨を発見できるということなんでしょうか?
内容をまだよく理解できてなくて、頓珍漢な質問になると思いますが...。
[0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0]
[0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0]
[0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1]
[1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0]
[0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1]
[1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1]
[1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0]
[0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0]
[0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1]
[1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1]
[1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0]
[0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1]
[1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0]
[0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0]
[0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1]
[1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0]
[0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1]
[1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1]
[1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0]
[0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1]
[1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0]
[0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0]
[0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1]
[1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1]
[1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0]
[0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1 0]
[0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0 1]
[1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 0]
[0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1]
[1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0 1]
[1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 0]
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月17日付け)
GAI さん、ちょっと見では、この計測ですと、嘘つきの検査官が最大5人までいても偽金貨
を特定できるようですね。1/3 が嘘ついても大丈夫って、すごいことです。とりあえず速報まで。
kuiperbelt さんからのコメントです。(令和6年10月18日付け)
31人の技術者に1~9,A~H,J~N,P~Xの名前をつけて、31個の金貨に、「あ」~「ま」の名
前をつけて、それぞれを以下のようにGF(2)上の4次元射影空間内の31個の点と31枚の超平
面に対応させます。各超平面内の15個の点が、該当する金貨を測定する15人の技術者に
相当します。
1:(0,0,0,0,1) 2:(1,0,0,0,1) 3:(0,1,0,0,1) 4:(1,1,0,0,1) 5:(0,0,1,0,1) 6:(1,0,1,0,1)
7:(0,1,1,0,1) 8:(1,1,1,0,1)
9:(0,0,0,1,1) A:(1,0,0,1,1) B:(0,1,0,1,1) C:(1,1,0,1,1) D:(0,0,1,1,1) E:(1,0,1,1,1)
F:(0,1,1,1,1) G:(1,1,1,1,1)
H:(1,0,0,0,0) J:(0,1,0,0,0) K:(1,1,0,0,0) L:(0,0,1,0,0) M:(1,0,1,0,0) N:(0,1,1,0,0) P:(1,1,1,0,0) Q:(0,0,0,1,0)
R:(1,0,0,1,0) S:(0,1,0,1,0) T:(1,1,0,1,0) U:(0,0,1,1,0) V:(1,0,1,1,0) W:(0,1,1,1,0)
X:(1,1,1,1,0)
あ:1,2,3,4,5,6,7,8,H,J,K,L,M,N,P
い:1,2,3,4,9,A,B,C,H,J,K,Q,R,S,T
う:1,2,5,6,9,A,D,E,H,L,M,Q,R,U,V
え:1,3,5,7,9,B,D,F,J,L,N,Q,S,U,W
お:9,A,B,C,D,E,F,G,H,J,K,L,M,N,P
か:5,6,7,8,D,E,F,G,H,J,K,Q,R,S,T
き:3,4,7,8,B,C,F,G,H,L,M,Q,R,S,T
く:2,4,6,8,A,C,E,G,J,L,N,Q,S,U,W
け:1,4,5,8,9,C,D,G,K,L,P,Q,T,U,X
こ:1,3,6,8,9,B,E,G,J,M,P,Q,S,V,X
さ:1,2,7,8,9,A,F,G,H,N,P,Q,R,W,X
し:1,3,5,7,A,C,E,G,J,L,N,R,T,V,X
す:1,2,5,6,B,C,F,G,H,L,M,S,T,W,X
せ:1,2,3,4,D,E,F,G,H,J,K,U,V,W,X
そ:2,3,6,7,A,B,E,F,K,L,P,Q,T,U,X
た:2,4,5,7,A,C,D,F,J,M,P,Q,S,V,X
ち:3,4,5,6,B,C,D,E,H,N,P,Q,R,W,X
つ:2,4,6,8,9,B,D,F,J,L,N,R,T,V,X
て:3,4,7,8,9,A,D,E,H,L,M,S,T,W,X
と:5,6,7,8,9,A,B,C,H,J,K,U,V,W,X
な:1,4,6,7,9,C,E,F,K,M,N,Q,T,V,W
に:1,4,5,8,A,B,E,F,K,L,P,R,S,V,W
ぬ:1,3,6,8,A,C,D,F,J,M,P,R,T,U,W
ね:1,2,7,8,B,C,D,E,H,N,P,S,T,U,V
の:2,3,5,8,A,B,D,G,K,M,N,Q,T,V,W
は:2,3,6,7,9,C,D,G,K,L,P,R,S,V,W
ひ:2,4,5,7,9,B,E,G,J,M,P,R,T,U,W
ふ:3,4,5,6,9,A,F,G,H,N,P,S,T,U,V
へ:1,4,6,7,A,B,D,G,K,M,N,R,S,U,X
ほ:2,3,5,8,9,C,E,F,K,M,N,R,S,U,X
ま:H,J,K,L,M,N,P,Q,R,S,T,U,V,W,X
対応する31ビット符号は以下のようになりますが、最小ハミング距離は16で、最大7人まで
が偽りの報告をしても偽金貨を特定できます。
[1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0],
[1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0],
[1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0],
[1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0],
[0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0],
[0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0],
[0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0],
[0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0],
[1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1],
[1,0,1,0,0,1,0,1,1,0,1,0,0,1,0,1,0,1,0,0,1,0,1,1,0,1,0,0,1,0,1],
[1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,1],
[1,0,1,0,1,0,1,0,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,0,1,0,1,0,1,0,1],
[1,1,0,0,1,1,0,0,0,0,1,1,0,0,1,1,1,0,0,1,1,0,0,0,0,1,1,0,0,1,1],
[1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1],
[0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1],
[0,1,0,1,1,0,1,0,0,1,0,1,1,0,1,0,0,1,0,0,1,0,1,1,0,1,0,0,1,0,1],
[0,0,1,1,1,1,0,0,0,0,1,1,1,1,0,0,1,0,0,0,0,1,1,1,1,0,0,0,0,1,1],
[0,1,0,1,0,1,0,1,1,0,1,0,1,0,1,0,0,1,0,1,0,1,0,0,1,0,1,0,1,0,1],
[0,0,1,1,0,0,1,1,1,1,0,0,1,1,0,0,1,0,0,1,1,0,0,0,0,1,1,0,0,1,1],
[0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1],
[1,0,0,1,0,1,1,0,1,0,0,1,0,1,1,0,0,0,1,0,1,1,0,1,0,0,1,0,1,1,0],
[1,0,0,1,1,0,0,1,0,1,1,0,0,1,1,0,0,0,1,1,0,0,1,0,1,1,0,0,1,1,0],
[1,0,1,0,0,1,0,1,0,1,0,1,1,0,1,0,0,1,0,0,1,0,1,0,1,0,1,1,0,1,0],
[1,1,0,0,0,0,1,1,0,0,1,1,1,1,0,0,1,0,0,0,0,1,1,0,0,1,1,1,1,0,0],
[0,1,1,0,1,0,0,1,0,1,1,0,1,0,0,1,0,0,1,0,1,1,0,1,0,0,1,0,1,1,0],
[0,1,1,0,0,1,1,0,1,0,0,1,1,0,0,1,0,0,1,1,0,0,1,0,1,1,0,0,1,1,0],
[0,1,0,1,1,0,1,0,1,0,1,0,0,1,0,1,0,1,0,0,1,0,1,0,1,0,1,1,0,1,0],
[0,0,1,1,1,1,0,0,1,1,0,0,0,0,1,1,1,0,0,0,0,1,1,0,0,1,1,1,1,0,0],
[1,0,0,1,0,1,1,0,0,1,1,0,1,0,0,1,0,0,1,0,1,1,0,0,1,1,0,1,0,0,1],
[0,1,1,0,1,0,0,1,1,0,0,1,0,1,1,0,0,0,1,0,1,1,0,0,1,1,0,1,0,0,1],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
31人の技術者に1~9,A~H,J~N,P~Xの名前をつけて、31個の金貨に、「あ」~「ま」の名
前をつけて、それぞれを以下のようにGF(5)上の射影平面内の31個の点と31本の直線に対
応させた場合も考えてみました。各直線内の6個の点が、該当する金貨を測定する6人の技
術者に相当します。
1:(0,0,1) 2:(1,0,1) 3:(2,0,1) 4:(3,0,1) 5:(4,0,1) 6:(0,1,1) 7:(1,1,1) 8:(2,1,1) 9:(3,1,1) A:(4,1,1) B:(0,2,1)
C:(1,2,1) D:(2,2,1) E:(3,2,1) F:(4,2,1) G:(0,3,1) H:(1,3,1) J:(2,3,1) K:(3,3,1) L:(4,3,1) M:(0,4,1) N:(1,4,1)
P:(2,4,1) Q:(3,4,1) R:(4,4,1) S:(1,0,0) T:(4,1,0) U:(3,1,0) V:(2,1,0)
W:(1,1,0) X:(0,1,0)
あ:1,2,3,4,5,S
い:6,7,8,9,A,S
う:B,C,D,E,F,S
え:G,H,J,K,L,S
お:M,N,P,Q,R,S
か:1,A,E,J,N,T
き:2,6,F,K,P,T
く:3,7,B,L,Q,T
け:4,8,C,M,R,T
こ:5,9,D,H,M,T
さ:1,9,C,L,P,U
し:2,A,D,G,Q,U
す:3,6,E,H,R,U
せ:4,7,F,J,M,U
そ:5,8,B,K,N,U
た:1,8,F,H,Q,V
ち:2,9,B,J,R,V
つ:3,A,C,K,M,V
て:4,6,D,L,N,V
と:5,7,E,G,P,V
な:1,7,D,K,R,W
に:2,8,E,L,M,W
ぬ:3,9,F,G,N,W
ね:4,A,B,H,P,W
の:5,6,C,J,Q,W
は:1,6,B,G,M,X
ひ:2,7,C,H,N,X
ふ:3,8,D,J,P,X
へ:4,9,E,K,Q,X
ほ:5,A,F,L,R,X
ま:S,T,U,V,W,X
1直線上には6点が存在し、どの2直線も1点を共有するので、1点を共有する2直線には互
いに異なる5点があることになります。対応する31ビット符号は以下のようになりますが、最
小ハミング距離は10で、最大4人までが偽りの報告をしても偽金貨を特定できます。
[1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0],
[1,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,0,1,0,0,0,0],
[0,1,0,0,0,1,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,0],
[0,0,1,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,1,0,0,0,0],
[0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,0,1,0,1,0,0,0,0],
[0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,0,0,1,0,0,0,0],
[1,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0],
[0,1,0,0,0,0,0,0,0,1,0,0,1,0,0,1,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0],
[0,0,1,0,0,1,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,1,0,0,1,0,0,0],
[0,0,0,1,0,0,1,0,0,0,0,0,0,0,1,0,0,1,0,0,1,0,0,0,0,0,0,1,0,0,0],
[0,0,0,0,1,0,0,1,0,0,1,0,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,1,0,0,0],
[1,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,0,1,0,0],
[0,1,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,1,0,0],
[0,0,1,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,0,1,0,0],
[0,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,1,0,0],
[0,0,0,0,1,0,1,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,0,0,1,0,0],
[1,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,1,0],
[0,1,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,1,0],
[0,0,1,0,0,0,0,0,1,0,0,0,0,0,1,1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0],
[0,0,0,1,0,0,0,0,0,1,1,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,1,0],
[0,0,0,0,1,1,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,1,0],
[1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,0,0,1],
[0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,0,1],
[0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,1],
[0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,1],
[0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,1],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1]
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月18日付け)
流速が増大していて、なかなか追いつけませんが...。
上記の GAI さんの 31 の解、不思議でなりません。ブロックデザインとして、どのような位
置づけなのか?巡回していますよね。
この手の解のデータベースをあたったのですが、登録されていませんでした。新発見?
GAI さんからのコメントです。(令和6年10月20日付け)
いくつでも作れそうです。
例えば、63×63で各行各列hammingweght=31
1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0
0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0
0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1
1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0
0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1
1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1
1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0
0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0
0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1
1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1
1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0
0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1
1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0
0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0
0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1
1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0
0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1
1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1
1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0
0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1
1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0
0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0
0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1
1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1
1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0
0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0
0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1
1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0
0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1
1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1
1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0
0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0
0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1
1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1
1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0
0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1
1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0
0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0
0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1
1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1
1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0
0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0
0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1
1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0
0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1
1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1
1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0
0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1
1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0
0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0
0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1
1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0
0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1
1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1
1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0
0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0
0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1 1
1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0 1
1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 0
0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1
1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0
0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0
0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月20日付け)
GAI さん、あとで秘訣をご教示下さい。
技術者が13人いるのならば、金貨は88枚でいけるでしょ?と教えられました。
まだ理解していません。
GAI さんからのコメントです。(令和6年10月21日付け)
第1行が
1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0
ですが、これは、
1(1)=10
10(10)=1001
1001(1001)=10010110
10010110(10010110)=1001011001101001
1001011001101001(1001011001101001)=10010110011010010110100110010110
10010110011010010110100110010110(10010110011010010110100110010110)
=1001011001101001011010011001011001101001100101101001011001101001
となるので、最後の1をカットして、63個の中に1が31個(0は32個)であるものを配置しており
ます。
あとは、これを一個ずつ左ローテーションして構成しております。こうして、63×63の行列に
してみたら、すべての行、列の digitsweight=31 のものが結果的に構成されました。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月21日付け)
GAI さん、秘訣をありがとうございます!まさかの Thue-Morse列 なのですね!これを巡回
させると!
GAI さんからのコメントです。(令和6年10月22日付け)
単に、88×88行列で各行各列が1が13個ずつ配列できるものは構成可能ですが、これが
限界という意味が私には理解できません。
(コンピュータによる出力のため2を0に読み替えて見てください。)
%01 = 2121221222122221222221222222122222212222222122222222122222222212222222222122222222222122
%02 = 2212122122212222122222122222212222221222222212222222212222222221222222222212222222222212
%03 = 2221212212221222212222212222221222222122222221222222221222222222122222222221222222222221
%04 = 1222121221222122221222221222222122222212222222122222222122222222212222222222122222222222
%05 = 2122212122122212222122222122222212222221222222212222222212222222221222222222212222222222
%06 = 2212221212212221222212222212222221222222122222221222222221222222222122222222221222222222
%07 = 2221222121221222122221222221222222122222212222222122222222122222222212222222222122222222
%08 = 2222122212122122212222122222122222212222221222222212222222212222222221222222222212222222
%09 = 2222212221212212221222212222212222221222222122222221222222221222222222122222222221222222
%10 = 2222221222121221222122221222221222222122222212222222122222222122222222212222222222122222
%11 = 2222222122212122122212222122222122222212222221222222212222222212222222221222222222212222
%12 = 2222222212221212212221222212222212222221222222122222221222222221222222222122222222221222
%13 = 2222222221222121221222122221222221222222122222212222222122222222122222222212222222222122
%14 = 2222222222122212122122212222122222122222212222221222222212222222212222222221222222222212
%15 = 2222222222212221212212221222212222212222221222222122222221222222221222222222122222222221
%16 = 1222222222221222121221222122221222221222222122222212222222122222222122222222212222222222
%17 = 2122222222222122212122122212222122222122222212222221222222212222222212222222221222222222
%18 = 2212222222222212221212212221222212222212222221222222122222221222222221222222222122222222
%19 = 2221222222222221222121221222122221222221222222122222212222222122222222122222222212222222
%20 = 2222122222222222122212122122212222122222122222212222221222222212222222212222222221222222
%21 = 2222212222222222212221212212221222212222212222221222222122222221222222221222222222122222
%22 = 2222221222222222221222121221222122221222221222222122222212222222122222222122222222212222
%23 = 2222222122222222222122212122122212222122222122222212222221222222212222222212222222221222
%24 = 2222222212222222222212221212212221222212222212222221222222122222221222222221222222222122
%25 = 2222222221222222222221222121221222122221222221222222122222212222222122222222122222222212
%26 = 2222222222122222222222122212122122212222122222122222212222221222222212222222212222222221
%27 = 1222222222212222222222212221212212221222212222212222221222222122222221222222221222222222
%28 = 2122222222221222222222221222121221222122221222221222222122222212222222122222222122222222
%29 = 2212222222222122222222222122212122122212222122222122222212222221222222212222222212222222
%30 = 2221222222222212222222222212221212212221222212222212222221222222122222221222222221222222
%31 = 2222122222222221222222222221222121221222122221222221222222122222212222222122222222122222
%32 = 2222212222222222122222222222122212122122212222122222122222212222221222222212222222212222
%33 = 2222221222222222212222222222212221212212221222212222212222221222222122222221222222221222
%34 = 2222222122222222221222222222221222121221222122221222221222222122222212222222122222222122
%35 = 2222222212222222222122222222222122212122122212222122222122222212222221222222212222222212
%36 = 2222222221222222222212222222222212221212212221222212222212222221222222122222221222222221
%37 = 1222222222122222222221222222222221222121221222122221222221222222122222212222222122222222
%38 = 2122222222212222222222122222222222122212122122212222122222122222212222221222222212222222
%39 = 2212222222221222222222212222222222212221212212221222212222212222221222222122222221222222
%40 = 2221222222222122222222221222222222221222121221222122221222221222222122222212222222122222
%41 = 2222122222222212222222222122222222222122212122122212222122222122222212222221222222212222
%42 = 2222212222222221222222222212222222222212221212212221222212222212222221222222122222221222
%43 = 2222221222222222122222222221222222222221222121221222122221222221222222122222212222222122
%44 = 2222222122222222212222222222122222222222122212122122212222122222122222212222221222222212
%45 = 2222222212222222221222222222212222222222212221212212221222212222212222221222222122222221
%46 = 1222222221222222222122222222221222222222221222121221222122221222221222222122222212222222
%47 = 2122222222122222222212222222222122222222222122212122122212222122222122222212222221222222
%48 = 2212222222212222222221222222222212222222222212221212212221222212222212222221222222122222
%49 = 2221222222221222222222122222222221222222222221222121221222122221222221222222122222212222
%50 = 2222122222222122222222212222222222122222222222122212122122212222122222122222212222221222
%51 = 2222212222222212222222221222222222212222222222212221212212221222212222212222221222222122
%52 = 2222221222222221222222222122222222221222222222221222121221222122221222221222222122222212
%53 = 2222222122222222122222222212222222222122222222222122212122122212222122222122222212222221
%54 = 1222222212222222212222222221222222222212222222222212221212212221222212222212222221222222
%55 = 2122222221222222221222222222122222222221222222222221222121221222122221222221222222122222
%56 = 2212222222122222222122222222212222222222122222222222122212122122212222122222122222212222
%57 = 2221222222212222222212222222221222222222212222222222212221212212221222212222212222221222
%58 = 2222122222221222222221222222222122222222221222222222221222121221222122221222221222222122
%59 = 2222212222222122222222122222222212222222222122222222222122212122122212222122222122222212
%60 = 2222221222222212222222212222222221222222222212222222222212221212212221222212222212222221
%61 = 1222222122222221222222221222222222122222222221222222222221222121221222122221222221222222
%62 = 2122222212222222122222222122222222212222222222122222222222122212122122212222122222122222
%63 = 2212222221222222212222222212222222221222222222212222222222212221212212221222212222212222
%64 = 2221222222122222221222222221222222222122222222221222222222221222121221222122221222221222
%65 = 2222122222212222222122222222122222222212222222222122222222222122212122122212222122222122
%66 = 2222212222221222222212222222212222222221222222222212222222222212221212212221222212222212
%67 = 2222221222222122222221222222221222222222122222222221222222222221222121221222122221222221
%68 = 1222222122222212222222122222222122222222212222222222122222222222122212122122212222122222
%69 = 2122222212222221222222212222222212222222221222222222212222222222212221212212221222212222
%70 = 2212222221222222122222221222222221222222222122222222221222222222221222121221222122221222
%71 = 2221222222122222212222222122222222122222222212222222222122222222222122212122122212222122
%72 = 2222122222212222221222222212222222212222222221222222222212222222222212221212212221222212
%73 = 2222212222221222222122222221222222221222222222122222222221222222222221222121221222122221
%74 = 1222221222222122222212222222122222222122222222212222222222122222222222122212122122212222
%75 = 2122222122222212222221222222212222222212222222221222222222212222222222212221212212221222
%76 = 2212222212222221222222122222221222222221222222222122222222221222222222221222121221222122
%77 = 2221222221222222122222212222222122222222122222222212222222222122222222222122212122122212
%78 = 2222122222122222212222221222222212222222212222222221222222222212222222222212221212212221
%79 = 1222212222212222221222222122222221222222221222222222122222222221222222222221222121221222
%80 = 2122221222221222222122222212222222122222222122222222212222222222122222222222122212122122
%81 = 2212222122222122222212222221222222212222222212222222221222222222212222222222212221212212
%82 = 2221222212222212222221222222122222221222222221222222222122222222221222222222221222121221
%83 = 1222122221222221222222122222212222222122222222122222222212222222222122222222222122212122
%84 = 2122212222122222122222212222221222222212222222212222222221222222222212222222222212221212
%85 = 2212221222212222212222221222222122222221222222221222222222122222222221222222222221222121
%86 = 1221222122221222221222222122222212222222122222222122222222212222222222122222222222122212
%87 = 2122122212222122222122222212222221222222212222222212222222221222222222212222222222212221
%88 = 1212212221222212222212222221222222122222221222222221222222222122222222221222222222221222
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月22日付け)
GAI さん、ありがとうございます。小さなモデルでは次のようになります。
ガイガーカウンター管 で 11 回計測する。(技術者ひとりにつき1回、技術者の総数は 11 、
うち0人~2人は嘘の報告をする)
このとき、22 枚の金貨のうち 1 枚の放射性物質を含む偽金貨を特定できる。
計測の準備には2通りの方法がある。
①少しづつ金貨を計測していき、その計測結果をもとにして次の計測の段取りをつける
②実際の計測の前に11人の技術者が計測する金貨を決定してしまう。
一昨日見つけてたまげたのですが、下記のように計測すれば②で22枚中1枚を特定でき
ます。
10111000100,
01011100010,
00101110001,
10010111000,
01001011100,
00100101110,
00010010111,
10001001011,
11000100101,
11100010010,
01110001001,
01000111011,
10100011101,
11010001110,
01101000111,
10110100011,
11011010001,
11101101000,
01110110100,
00111011010,
00011101101,
10001110110,
たまげた理由。
②のやりかたのシバリでは、kuiperbelt さんも、私も、最大 16 枚の金貨中から偽金貨1枚を
みつける方法を過去に投稿して来ました。
符号長11で最小ハミング距離が 5 以上の系では、符号の最大総数は 16 だろうという雰囲
気で。ところが上ではそれを6枚ぶん上回りました。
もっというと、all 0 と all 1 を勘定にいれれば 24 枚となるところに驚いております。
で、今回の 88 枚の件ですが、
技術者を13人とし、計測の方法は ① とする、ということとなります。嘘つきの数は変えませ
ん。少しづつ、計測しながら、その結果をみながら、次に測定する金貨を定めていく、しかも、
いつ嘘をつかれるか不定である、そのような状況下で、88 枚も処理できるなんて!??
この 88 は 先ほどの 22 の 4 倍になっています。なにか関係があるかどうか探っています。
wikipedia の プロトキン限界 の項目では、符号長 11 最小ハミング距離が 5 の二元コード
の符号語数が 最大 24 となり、やった!みつけたぞ!と大喜びしておりましたが、これの限
界の公式は、どうやら間違いのようで。ぐはっ。
りらひいさんからのコメントです。(令和6年10月23日付け)
方法①なら、こんな感じでどうしょう。行き当たりばったりで組んだので汚いですが……。
金貨を4つのグループA,B,C,Dに振り分けながら測定を行っていく。
・グループA:偽金貨だった場合に現在までの全員が正しく報告をしている金貨の集合
(偽金貨である可能性がある)
・グループB:偽金貨だった場合に現在までの一人が誤った報告をしている金貨の集合
(偽金貨である可能性がある)
・グループC:偽金貨だった場合に現在までの二人が誤った報告をしている金貨の集合
(偽金貨である可能性がある)
・グループD:偽金貨だった場合に現在までの三人が誤った報告をしている金貨の集合
(偽金貨である可能性はない)
グループA,B,C,Dは、最上位:A→B→C→D:最下位となるように順位付けしておく。
各技術者の測定結果に応じて次のように金貨のグループを変更する。
陽性⇒測定した金貨は今のグループに残す。測定しなかった金貨を一つ下位のグループに
移す(グループDの金貨を除く)。
陰性⇒測定した金貨を一つ下位のグループに移す。測定しなかった金貨は今のグループに
残す。
最初は、88枚すべてグループAである。
測定を繰り返してグループDが87枚になったら、残った1枚が偽金貨である。
測定方法は以下の通り(あくまでも一例である)。
丸数字は測定方法の場合分けであり、前の人までの測定結果によりどれかを選択していく。
丸数字のあとのA,B,C,Dの数字は、測定前の各グループの金貨の枚数。
各グループからそれぞれ決められた枚数を選んでまとめて測定する。グループ内でどの金
貨を選ぶかは自由。
[1人目]
① A:88, B:0, C:0, D:0 ⇒ Aから44枚 測定
・陽性/陰性 → 2人目①へ
[2人目]
① A:44, B:44, C:0, D:0 ⇒ Aから22枚、Bから22枚 測定
・陽性/陰性 → 3人目①へ
[3人目]
① A:22, B:44, C:22, D:0 ⇒ Aから11枚、Bから22枚、Cから11枚 測定
・陽性/陰性 → 4人目①へ
[4人目]
① A:11, B:33, C:33, D:11 ⇒ Aから6枚、Bから15枚、Cから12枚 測定
・陽性 → 5人目①へ
・陰性 → 5人目②へ
[5人目]
① A:6, B:20, C:30, D:32 ⇒ Aから3枚、Bから10枚、Cから15枚 測定
・陽性/陰性 → 6人目①へ
② A:5, B:24, C:36, D:23 ⇒ Aから3枚、Bから11枚、Cから12枚 測定
・陽性 → 6人目①へ
・陰性 → 6人目②へ
[6人目]
① A:3, B:13, C:25, D:47 ⇒ Aから2枚、Bから5枚、Cから12枚 測定
・陽性 → 7人目①へ
・陰性 → 7人目②へ
② A:2, B:16, C:35, D:35 ⇒ Aから1枚、Bから9枚、Cから11枚 測定
・陽性 → 7人目②へ
・陰性 → 7人目③へ
[7人目]
① A:2, B:6, C:20, D:60 ⇒ Aから1枚、Bから3枚、Cから10枚 測定
・陽性/陰性 → 8人目①へ
② A:1, B:10, C:18, D:59 ⇒ Aから1枚、Bから4枚、Cから7枚 測定
・陽性 → 8人目①へ
・陰性 → 8人目②へ
③ A:1, B:8, C:33, D:46 ⇒ Aから1枚、Bから4枚、Cから9枚 測定
・陽性 → 8人目①へ
・陰性 → 8人目③へ
[8人目]
① A:1, B:4, C:13, D:70 ⇒ Aから1枚、Bから1枚、Cから6枚 測定
・陽性 → 9人目①へ
・陰性 → 9人目②へ
② A:0, B:7, C:15, D:66 ⇒ Bから4枚、Cから5枚 測定
・陽性 → 9人目②へ
・陰性 → 9人目③へ
③ A:0, B:5, C:28, D:55 ⇒ Bから3枚、Cから12枚 測定
・陽性 → 9人目③へ
・陰性 → 9人目④へ
[9人目]
① A:1, B:1, C:9, D:77 ⇒ Aから1枚、Bから0枚、Cから3枚 測定
・陽性 → 10人目①へ
・陰性 → 10人目②へ
② A:0, B:4, C:8, D:76 ⇒ Bから2枚、Cから4枚 測定
・陽性/陰性 → 10人目②へ
③ A:0, B:3, C:14, D:71 ⇒ Bから2枚、Cから5枚 測定
・陽性 → 10人目②へ
・陰性 → 10人目③へ
④ A:0, B:2, C:19, D:67 ⇒ Bから1枚、Cから10枚 測定
・陽性 → 10人③目へ
・陰性 → 10人④目へ
[10人目]
① A:1, B:0, C:4, D:83 ⇒ Aから1枚 測定
・陽性 → 結論①へ
・陰性 → 11人目①へ
② A:0, B:2, C:6, D:80 ⇒ Bから1枚、Cから3枚 測定
・陽性/陰性 → 11人目①へ
③ A:0, B:1, C:11, D:76 ⇒ Bから1枚、Cから4枚 測定
・陽性 → 11人目①へ
・陰性 → 11人目③へ
④ A:0, B:1, C:10, D:77 ⇒ Bから1枚、Cから3枚 測定
・陽性 → 11人目②へ
・陰性 → 11人目③へ
[11人目]
① A:0, B:1, C:4, D:83 ⇒ Bから1枚、Cから1枚 測定
・陽性 → 12人目①へ
・陰性 → 12人目②へ
② A:0, B:1, C:3, D:84 ⇒ Bから1枚、Cから1枚 測定
・陽性 → 12人目①へ
・陰性 → 12人目③へ
③ A0:, B:0, C:8, D:80 ⇒ Cから4枚 測定
・陽性/陰性 → 12人目②へ
[12人目]
① A:0, B:1, C:1, D:86 ⇒ Bから1枚 測定
・陽性 → 結論②へ
・陰性 → 13人目①へ
② A:0, B:0, C:4, D:84 ⇒ Cから2枚 測定
・陽性/陰性 → 13人目①へ
③ A:0, B:0, C:3, D:85 ⇒ Cから2枚 測定
・陽性 → 13人目①へ
・陰性 → 結論③へ
[13人目]
① A:0, B:0, C:2, D:86 ⇒ Cから1枚 測定
・陽性/陰性 → 結論③へ
[結論]
① A:1, B:0, C:0, D:87 ⇒ Aの1枚が偽金貨確定
② A:0, B:1, C:0, D:87 ⇒ Bの1枚が偽金貨確定
③ A:0, B:0, C:1, D:87 ⇒ Cの1枚が偽金貨確定
※12人目までに偽金貨が確定した場合、残りの技術者に偽金貨だけを測定させれば嘘つき
を特定することもできる。
各測定の枚数は、条件を満たすものをとりあえずで決めただけなので、ほかにも測定方法
はいろいろありそうです。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年10月24日付け)
りらひいさん!これ、大変に興味深いです。!ありがとうございます。勉強させてください。
■上界と上限の違い
上界 (Upper Bound): 集合 A の上界とは、集合のすべての要素がその数以下であるような
数のことです。上界は複数存在する可能性があります。
上限 (Supremum): 上限は、上界の中で最小のものを指します。つまり、上限より小さい数は
上界ではなくなります。上限は一意に定まります。
例として、集合 (0,1) の場合、1が上限ですが、2や3も上界です。
さて、上記の投稿にて、バイナリコードにおける、符号長 11 、最小ハミング距離が 5 であっ
て、符号語の数が 24 であるものの具体的な構成例をお示しいたしました。
昨夜にみつけたのですけれども、バイナリコードにおける、符号長 11 、最小ハミング距離
が 5 という条件のもとで、符号語の数のひとつの上界として 24 が既に証明されているよう
です。(→ Table of general binary codes)
このページに記載の上界の一覧表では、符号長 n . 最小ハミング距離 d のもとで、符号語
数 A₂(n,d) がまとめられています。ただし、d が偶数のときのみです。
d が奇数の時には以下の公式を使います。
A₂(n-1,2e-1) = A₂(n,2e)
そこで、n=12, e=3 とすると、A₂(11,5) = A₂(12,6) となります。
A₂(11,5)の値を知りたかったので、一覧表からA₂(12,6)を引きます。A₂(12,6) = 24 が得ら
れました。すなわち、A₂(11,5) = 24 となります。
バイナリコードにおける、符号長 11 、最小ハミング距離が 5 という条件のもとで、符号語
の数のひとつの上界として 24 が判明したということとなります。
あらためまして、先日みつけた符号を下記に再掲いたします。
00000000000,
10111000100,
01011100010,
00101110001,
10010111000,
01001011100,
00100101110,
00010010111,
10001001011,
11000100101,
11100010010,
01110001001,
01000111011,
10100011101,
11010001110,
01101000111,
10110100011,
11011010001,
11101101000,
01110110100,
00111011010,
00011101101,
10001110110,
11111111111,
24 という上界は上限でもあったと判明したこととなります。
(個人的に嬉しくてイキっております、ご寛恕を願います)
Dengan kesaktian Indukmu さんからのコメントです。(令和6年11月1日付け)
以下の問題に解があるとのお知らせをもらいました。金貨13枚から51枚も増えています。
64 枚の金貨があり、そのうち1枚は放射性物質を含む偽物です。この偽物をガイガーカウ
ンターを用いた一連の測定で特定する課題です。問題は以下のように構成されています:
金貨:64 枚の金貨があり、1 から 64 まで番号が振られています。ちょうど 1 枚が偽物です。
偽物の特性:偽の金貨は放射性物質を含んでおり、ガイガーカウンターで検出可能です。
技術者:13人の技術者が測定を行います。
測定プロセス:各技術者は 64 枚の金貨のうち一部を選んで測定します。技術者は選ばれた
金貨をガイガーカウンターで同時に検査します。ガイガーカウンターは、選ばれた金貨の中に
偽物が含まれている場合にのみ反応します。測定結果は、その技術者のみが知っています。
測定の制約:各技術者は正確に 1 回だけ測定を行い、合計 13 回の測定が行われます。
報告:各測定の後、技術者は「陽性」(放射線が検出された)または「陰性」(放射線が検出
されなかった)と報告します。
信頼性の問題:技術者のうち最大 2 人までが、意図的な欺瞞や偶発的な誤りにより不正確
な報告をする可能性があります。
目標:最大 2 件の不正確な報告があったとしても、偽の金貨を確実に特定することが目標
です。
割とまじめに計算機を使いましたが、せいぜいで 40 枚くらいまでで………、64 枚解を求め
るためには本格的なバックトラッキングをしなくては解けない気がしてきまして慄いています。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年11月6日付け)
上記の答です。符号語数が64で符号長が13、最小ハミング距離が5となっています。
0000000000000
0000000011111
0000011100011
0000101101100
0000110110101
0000111011010
0001001110110
0001110001001
0010010101110
0010101010001
0011001001011
0011010010010
0011011111101
0011100100111
0011100111000
0011111000100
0100010111000
0100101000111
0101000101101
0101011001110
0101011010001
0101100010100 |
|
0101101111011
0101110100010
0110000110011
0110001011100
0110010000101
0110100001010
0110111101001
0110111110110
0111001100000
0111110011111
1000011010100
1000100101011
1001000110001
1001010000111
1001011101000
1001101000010
1001101011101
1001110111110
1010001100101
1010001111010
1100011111111
1100101110000 |
|
1100110001100
1100110010011
1101000011010
1101111100101
1110011000010
1110100111101
1111001010111
1111010101011
1111010110100
1111100000001
1111101101110
1111111011000
1010010011001
1010100010110
1010110100000
1010111001111
1011000001100
1011111110011
1100000100110
1100001001001 |
どうやっても私には独力では作れませんでした。ガックシ…… 符号語数が32までならスグ
に作れるのに。
(参考) OEIS の 「A005865」にてわかることとして、A005865(13, 5) = A005865(14, 6) = 64
となります。
嘘報告が最大2(すなわち5/2の整数部分)あっても13回測れば、64枚から1枚の偽金貨を
特定できるということなので、その具体的な方法は?というストーリーなのでした。
Dengan kesaktian Indukmu さんからのコメントです。(令和6年12月1日付け)
13人いれば、そのうち最大2名が嘘をついても、64枚の金貨を処理できるだろう、の件
です。既にお示ししましたように、知人から解を教えてもらったもののその背景には何が有
るのか解らずに彷徨っております。普通に作ると32枚が限界。
漸く、このほど古い論文をみつけました。
An optimum nonlinear code
code
Alan W. Nordstrom ,John P. Robinson
https://www.sciencedirect.com/science/article/pii/S0019995867908352
これに書いてあることを猿真似して、最小ハミング距離が5でありながら14ビットで128もの
符号語数を実現する方法をメモしておきたく存じます。
情報ビットが7、冗長ビットが7、前者をX、後者をYとしたときに、エンコード方法は以下とな
ります。なお、「⊕」は排他的論理和、「 ⋅ 」は論理積です。
X₀∥X₁∥X₂∥X₃∥X₄∥X₅∥X₆
⇒
X₀∥X₁∥X₂∥X₃∥X₄∥X₅∥X₆∥Y₀∥Y₁∥Y₂∥Y₃∥Y₄∥Y₅∥Y₆
ただし、
Y₀ = X₆ ⊕ X₀ ⊕ X₁ ⊕ X₃ ⊕ ((X₀ ⊕ X₄) ⋅ (X₁ ⊕ X₂ ⊕ X₃ ⊕ X₅)) ⊕ ((X₁ ⊕ X₂) ⋅ (X₃ ⊕ X₅))
Y₁ = X₀ ⊕ X₁ ⊕ X₂ ⊕ X₄ ⊕ ((X₁ ⊕ X₅) ⋅ (X₂ ⊕ X₃ ⊕ X₄ ⊕ X₆)) ⊕ ((X₂ ⊕ X₃) ⋅ (X₄ ⊕ X₆))
Y₂ = X₁ ⊕ X₂ ⊕ X₃ ⊕ X₅ ⊕ ((X₂ ⊕ X₆) ⋅ (X₃ ⊕ X₄ ⊕ X₅ ⊕ X₀)) ⊕ ((X₃ ⊕ X₄) ⋅ (X₅ ⊕ X₀))
Y₃ = X₂ ⊕ X₃ ⊕ X₄ ⊕ X₆ ⊕ ((X₃ ⊕ X₀) ⋅ (X₄ ⊕ X₅ ⊕ X₆ ⊕ X₁)) ⊕ ((X₄ ⊕ X₅) ⋅ (X₆ ⊕ X₁))
Y₄ = X₃ ⊕ X₄ ⊕ X₅ ⊕ X₀ ⊕ ((X₄ ⊕ X₁) ⋅ (X₅ ⊕ X₆ ⊕ X₀ ⊕ X₂)) ⊕ ((X₅ ⊕ X₆) ⋅ (X₀ ⊕ X₂))
Y₅ = X₄ ⊕ X₅ ⊕ X₆ ⊕ X₁ ⊕ ((X₅ ⊕ X₂) ⋅ (X₆ ⊕ X₀ ⊕ X₁ ⊕ X₃)) ⊕ ((X₆ ⊕ X₀) ⋅ (X₁ ⊕ X₃))
Y₆ = X₅ ⊕ X₆ ⊕ X₀ ⊕ X₂ ⊕ ((X₆ ⊕ X₃) ⋅ (X₀ ⊕ X₁ ⊕ X₂ ⊕ X₄)) ⊕ ((X₀ ⊕ X₁) ⋅ (X₂ ⊕ X₄))
とします。
これをプログラムで実装して出力したところ、確かに所望のものができました。
よもやよもや論理積が使われているとは……。
エンコード後にX₀が0のものだけを取り出すと64件の符号語数となり、X₀はダミーと成り下
がりましたので、これを除去すれば、符号長が13、最小ハミング距離が5となります。これで
私が欲しかった実物を得ることができました。
0000000000000
0000011001011
0000100010111
0000111100110
0001000101110
0001011111000
0001101001101
0001110100001
0010001011100
0010010101101
0010101110001
0010110111010
0011000011011
0011011110111
0011101000010
0011110010100 |
0100000111001
0100011010101
0100101011010
0100110001100
0101001100011
0101010010010
0101101110100
0101110111111
0110000110110
0110011100000
0110101101111
0110110000011
0111000000101
0111011001110
0111100101000
0111111011001 |
1000001110010
1000010011110
1000100101011
1000111111101
1001000110101
1001011000100
1001100011000
1001111010011
1010001000111
1010010010001
1010100100100
1010111001000
1011001101001
1011010100010
1011101111110
1011110001111 |
1100001101100
1100010100111
1100101000001
1100110110000
1101001011111
1101010001001
1101100000110
1101111101010
1110000001010
1110011111011
1110100011101
1110111010110
1111001010000
1111010111100
1111100110011
1111111100101 |
Dengan kesaktian Indukmu さんからのコメントです。(令和7年3月7日付け)
Fake coins and a magic bag について、https://jkoizumi144.com/puzzles.html の冒頭に
次のようなパズルがあります。
<引用開始>
1. Fake coins and a magic bag
There are 7 gold coins and 9 silver coins. Among them, there is one fake
gold coin and one
fake silver coin. You want to identify these fake coins using a magic bag. When you put coins
into the magic bag and cast a spell, it emits a suspicious glow only if
both fake coins are inside
the bag. How many times do you need to cast the spell to determine both
fake coins?
<引用終わり>
① 5 回の呪文の詠唱では無理だという考察をします。
バッグが光る・光らないの1ビットの情報を5つ集めても、最大で 2^5 = 32 通りの分別がで
きるにすぎません。一方において、金銀の偽コインのありうるケースを数えあげると、7✕9=63
です。32 < 63 ですから、5 回の呪文の詠唱では無理そうと判断できます。
② 7回の詠唱で偽コインをつきとめる方法はあります。(省略)
③ 6回の詠唱ですますクレバーな方法があるのかどうか気になります。
63 < 2^6 = 64 ですから、《コレだけでは良い方法が無いとは断言できない》という…パズル
としては良い線を突いている感じがします。
実際、金が8枚、銀が8枚だと、6回の詠唱ですます方法はありますので、こちらが元のパズ
ルの姿で、それをひねって金7枚銀9枚に直してあるような……このヒネリにどんな意図があ
るのか頭を傾げています。
皆様のお知恵をお貸しください。
Dengan kesaktian Indukmu さんからのコメントです。(令和7年3月12日付け)
金7枚銀9枚のケースでは、6回の呪文詠唱で確実に偽コインを特定できると判明いたし
ました。難しく考えていたためにどツボに嵌っていたようです。お騒がせいたしました。
Dengan kesaktian Indukmu さんからのコメントです。(令和7年3月13日付け)
せっかくですので、金3枚、銀5枚のケースで、呪文詠唱4回のやり方をひとつご案内させ
ていただきます。
金を、G1、G2、G3 、銀を、S1、S2、S3、S4、S5 とします。偽コインのありうるケースは
15通りです。下図をご覧ください。
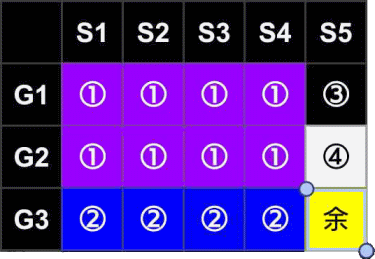
1回目の計測では①をカバーするように袋にいれて呪文を唱えます。袋が光れば、残り3回
の呪文で①のなかにある偽コインペアを確定させる課題はイージーです。
1回目の計測で光らない場合には次のステップに行きます。
2回目の計測では②をカバーするように袋にいれて呪文を唱えます。袋が光れば、残り2回
の呪文で②のなかにある偽コインペアを確定させる課題はイージーです。
2回目の計測で光らない場合には次のステップに行きます。
3回目の計測では③をカバーするように袋にいれて呪文を唱えます。袋が光れば偽コイン
ペアは確定です。(G1:S5)
3回目の計測で光らない場合には次のステップに行きます。
4回目の計測では④をカバーするように袋にいれて呪文を唱えます。袋が光れば偽コイン
ペアは確定です。(G2:S5)
4回目の計測で光らない場合には偽コインペアは確定です。(G3:S5)
なお、上記のやり方は容易に拡張できて、金7枚、銀9枚のケースで呪文6回で済ませる方
法があることがわかります。
Dengan kesaktian Indukmu さんからのコメントです。(令和7年3月15日付け)
金7枚、銀9枚のケースの図解も作りました。偽コインのペアが
⑤に含まれていれば残り5回の詠唱で確定。
さもなければ、④に含まれていれば残り4回の詠唱で確定。
さもなければ、③に含まれていれば残り3回の詠唱で確定。
さもなければ、②に含まれていれば残り2回の詠唱で確定。
さもなければ、①に含まれていれば残り1回の詠唱で確定。
さもなければ、※で確定
ということになります。
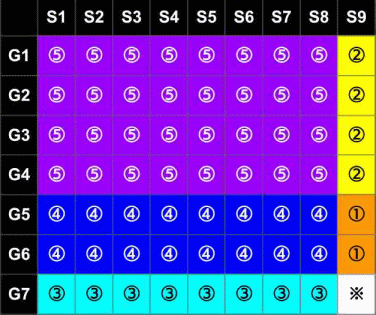
Dengan kesaktian Indukmu さんからのコメントです。(令和7年4月9日付け)
ふと思い立ちまして、chatgpt-4o-latest-20250326 に対して、下記のように出題しましたが、
誤答を返して来ました。なお、英文なのは、そのほうが生成AIにとって理解しやすいとわかっ
たからです。(誤答についてはナンセンスなので省略いたします。)
出題内容の下には、私がいま取り組んでいることも付記させていただきます。皆さんにご助
力を願えれば幸いです。よろしくお願い申し上げます。
♦出題内容♦
Fake Coins and a Magic Bag
You have a collection of 9 coins in total: 3 gold coins, 3 silver coins,
and 3 bronze coins.
Among these, exactly one gold coin, exactly one silver coin, and exactly
one bronze coin
are counterfeit.
Assume that the three coins of each metal are distinguishable (e.g., labeled G_1, G_2, G_3,
S_1, S_2, S_3, B_1, B_2, B_3).
You are provided with a magic bag that has the following property:
When you place any subset of coins into the bag and cast a spell, the bag
glows if and only
if the subset contains all three counterfeit coins simultaneously, regardless
of any additional
genuine coins that might be included.
If the subset contains only one, only two, or none of the counterfeit coins, the bag does
not glow.
All tests are deterministic and error-free. There are no restrictions on
how many or which
coins you may include in a single test, and coins may be reused in multiple
tests.
Your task is to devise a strategy that is guaranteed to identify all three
counterfeit coins
using no more than 5 tests.
Justify your answer with a logical or mathematical argument.
♦出題内容はここまで♦
♥私が今もがいていること♥
この出題について、どのようなヒント(誘導)を追加すれば生成AI(chatgptなど)が正解に辿り
着くか工夫をしているのですが悪戦苦闘しております。
皆さんに伺いたいのですが、なにか良いアイデアはないものでしょうか?
Dengan kesaktian Indukmu さんからのコメントです。(令和7年4月10日付け)
申し遅れました。決定木を求めてほしかったんです。下記の図のような、分割統治戦略で
二分木を作り、それぞれの枝において分析に必要な情報ビットが過度に大きくならないよう
に。
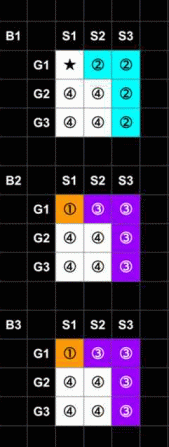
以下、工事中!




