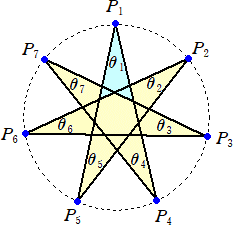
ばしで、次の点を次々と結んでいくと、一つの閉じた閉路が出来上がる。
(星が輝いているような図形)
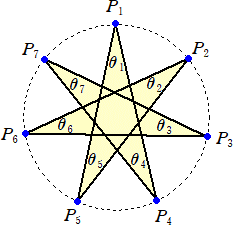
この時、点がある位置 P1、P2、P3、P4、P5、P6、P7 にできる線を引いた直線で作られる
7つの部分が作るそれぞれの角度をθi (i=1、2、3、・・・、7) とすれば、必ず、
∑[i=1,7]θi=180°
が起こる。(一応これは証明できたと自分では感じています。)
(→ 参考:「星形の内角の和」)
ところで、同じ設定で、ある点から1つ飛ばしで、次の点を次々と結んでいくと、同じように、
一つの閉じた閉路が出来上がる。(ゴツゴツした岩のような図形)
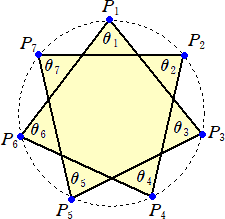
この図形に対するθiにおいては、
∑[i=1,7]θi=540°
が起こりそうなんです。そうとしか言えないのは、実験をして分度器で計測して予想している
だけで、証明がわからないのです。
何方かウソか真か決着を願います。
DD++ さんからのコメントです。(令和5年6月13日付け)
真です。
四角形の外角の大きさは、残り3つの内角の和から 180° を引いた値になります。それを
用いると、P7 のところにできる三角形の3つの内角が、
θ1+θ3+θ5-180°、θ2+θ4+θ6-180°、θ7
と表され、これらの和が 180° であることから示されます。
GAI さんからのコメントです。(令和5年6月13日付け)
わ~!なるほど。三角形の外角を拡張させて考えれば、スーと解けちゃうんですね。頭の
中には外角と言えば、てっきり三角形しか結びつけられていないことに縛られていることに
気付かされました。
壊れた扉さんからのコメントです。(令和5年6月13日付け)
真ですね。
簡易的には、円周上にP1~P7まで適当に点を取ると、
θ1=∠P1=弧P3P4の円周角+弧P4P5の円周角+弧P5P6の円周角
θ2=∠P2=弧P4P5の円周角+弧P5P6の円周角+弧P6P7の円周角
θ3=∠P3=弧P5P6の円周角+弧P6P7の円周角+弧P7P1の円周角
θ4=∠P4=弧P6P7の円周角+弧P7P1の円周角+弧P1P2の円周角
θ5=∠P5=弧P7P1の円周角+弧P1P2の円周角+弧P2P3の円周角
θ6=∠P6=弧P1P2の円周角+弧P2P3の円周角+弧P3P4の円周角
θ7=∠P7=弧P2P3の円周角+弧P3P4の円周角+弧P4P5の円周角
よって、∑[i=1,7]θi
=3(弧P1P2の円周角+弧P2P3の円周角+弧P3P4の円周角+弧P4P5の円周角
+弧P5P6の円周角+弧P6P7の円周角+弧P7P1の円周角)
=3×全円の円周角=3×180°=540°
厳密には、DD++ さんの解法を使えば良いですね。
(以前に解説していたら出禁になった事があるので止めておきます。)
また、2つ飛ばしの方は、2つの三角形の内対角の和とブーメランの定理を使うと簡単に示
せますね。
(コメント) ブーメランの定理を用いて、証明に挑戦してみた。