丒摍妏嫟栶揰偲摍嫍棧嫟栶揰丂丂丂 丂 丂 丂 丂 丂傝傜傂偄巵
丂嶐擭偐傜偺巹偺屄恖揑側僽乕儉偼丄嶰妏宍偵娭偡傞偁傟偙傟偱丄崱傕宲懕偟偰偄傑偡丅
悢擔慜偵傆偲栤戣傪巚偄偮偄偨偺偱彂偄偰傒傑偡丅偨偩偟丄栤戣偼嶌傝傑偟偨偑帺暘偱夝
偄偰偼偄側偄偺偱夝摎偼梡堄偟偰偄傑偣傫丅
乮偙偺栤戣偺撪梕傪娷傓傛傝堦斒揑側柦戣偑惉傝棫偮偙偲偼妋擣偟偰偄傑偡丅乯
乮慜採抦幆偦偺侾乯丂摍妏嫟栶揰 (isogonal conjugate)
丂嶰妏宍ABC偺奺曈偍傛傃偦偺墑挿慄偺忋偵側偄揰P傪偲傞丅
丂妏A偺擇摍暘慄偵娭偡傞捈慄AP偺嬀塮傪捈慄俴
丂妏B偺擇摍暘慄偵娭偡傞捈慄BP偺嬀塮傪捈慄俵
丂妏C偺擇摍暘慄偵娭偡傞捈慄CP偺嬀塮傪捈慄俶
偲偡傞偲丄俁杮偺捈慄俴丄俵丄俶偼侾揰俻偱岎傢傞丅偙偺岎揰傪(嶰妏宍ABC偵娭偡傞)揰P偺
摍妏嫟栶揰偲偄偆丅
丂丂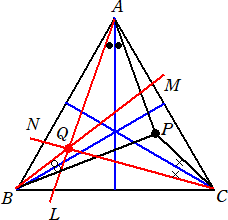
丂乽俁杮偺捈慄俴丄俵丄俶偑侾揰俻偱岎傢傞乿偙偲偼丄師偺傛偆偵丄僠僃僶偺掕棟傪梡偄偰帵偝
傟傞丅
乮徹柧乯丂捈慄俙俹偲曈俛俠偺岎揰傪俢偲偍偔丅傑偨丄佢俹俙俛亖兛丂偲偍偔丅偙偺偲偒丄
丂俛俢 丗 俢俠亖仮俙俛俢 丗 仮俙俢俠亖乮侾/俀乯俙俛丒俙俢倱倝値兛 丗 乮侾/俀乯俙俠丒俙俢倱倝値乮俙亅兛乯
偡側傢偪丄丂俛俢 丗 俢俠亖俙俛倱倝値兛 丗 俙俠倱倝値乮俙亅兛乯
丂摨條偵丄捈慄俛俹偲曈俠俙偺岎揰傪俤偲偍偔丅傑偨丄佢俹俛俠亖兝丂偲偍偔丅偙偺偲偒丄
丂俠俤 丗 俤俙亖BC倱倝値兝 丗 俛俙倱倝値乮俛亅兝乯
捈慄俠俹偲曈俙俛偺岎揰傪俥偲偍偔丅傑偨丄佢俹俠俙亖兞丂偲偍偔丅偙偺偲偒丄
丂俙俥 丗 俥俛亖俠俙倱倝値兞 丗 俠俛倱倝値乮俠亅兞乯
丂俁捈慄俙俹丄俛俹丄俠俹偑侾揰偱岎傢傞偺偱丄僠僃僶偺掕棟偵傛傝丄
丂乮俙俥/俥俛乯丒乮俛俢/俢俠乯丒乮俠俤/俤俙乯亖侾丂側偺偱丄
乮俠俙倱倝値兞乯/乮俠俛倱倝値乮俠亅兞乯乯丒乮俙俛倱倝値兛乯/乮俙俠倱倝値乮俙亅兛乯乯丒乮BC倱倝値兝乯/乮俛俙倱倝値乮俛亅兝乯乯亖侾
偡側傢偪丄乮倱倝値兞乯/乮倱倝値乮俠亅兞乯乯丒乮倱倝値兛乯/乮倱倝値乮俙亅兛乯乯丒乮倱倝値兝乯/乮倱倝値乮俛亅兝乯乯亖侾
乮俠俛倱倝値兞乯/乮俠俙倱倝値乮俠亅兞乯乯丒乮俙俠倱倝値兛乯/乮俙俛倱倝値乮俙亅兛乯乯丒乮俛俙倱倝値兝乯/乮俛俠倱倝値乮俛亅兝乯乯亖侾
偑惉傝棫偮丅捈慄俴偲曈俛俠偺岎揰傪俢乫丄捈慄俵偲曈俠俙偺岎揰傪俤乫丄捈慄俶偲曈俙俛偺岎揰
傪俥乫偲偍偔偲丄忋婰偺摍幃偼丄乮俥乫俛/俙俥乫乯丒乮俢乫俠/俛俢乫乯丒乮俤乫俙/俠俤乫乯亖侾
丂偡側傢偪丄丂乮俙俤乫/俤乫俠乯丒乮俠俢乫/俢乫俛乯丒乮俛俥乫/俥乫俙乯亖侾丂偑惉傝棫偮偙偲傪堄枴偡傞丅
傛偭偰丄僠僃僶偺掕棟傛傝丄俁捈慄俴丄俵丄俶偼侾揰俻偱岎傢傞丅丂丂乮徹廔乯
丂忋婰偺徹柧偵偮偄偰丄乽尫偵懳偡傞僠僃僶偺掕棟乿傪梡偄傞偲丄傕偭偲僄儗僈儞僩偵帵偡偙偲
偑弌棃傞丅乮椷榓俆擭俇寧俀侾擔晅偗乯
丂丂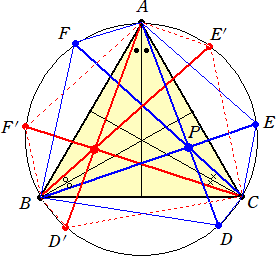
乮暿徹乯丂尫偵懳偡傞僠僃僶偺掕棟傛傝丄丂乮俙俥/俥俛乯丒乮俛俢/俢俠乯丒乮俠俤/俤俙乯亖侾
戣堄傛傝丄佢俙俠俥亖佢佢俛俠俥乫丂側偺偱丄丂俙俥亖俛俥乫
丂佢俛俠俥亖佢俥乫俠俙丂側偺偱丄丂俛俥亖俥乫俙
丂佢俛俙俢亖佢俠俙俢乫丂側偺偱丄丂俛俢亖俠俢乫
丂佢俢俙俠亖佢俢乫俙俛丂側偺偱丄丂俢俠亖俢乫俛
丂佢俠俛俤亖佢俙俛俤乫丂側偺偱丄丂俠俤亖俙俤乫
丂佢俤俛俙亖佢俤乫俛俠丂側偺偱丄丂俤俙亖俤乫俠
丂傛偭偰丄丂乮俛俥乫/俥乫俙乯丒乮俠俢乫/俢乫俛乯丒乮俙俤乫/俤乫俠乯亖侾丂傛傝丄
丂乮俙俤乫/俤乫俠乯丒乮俠俢乫/俢乫俛乯丒乮俛俥乫/俥乫俙乯亖侾丂偑尵偊傞丅
丂偙偺偙偲偼丄尫偵懳偡傞僠僃僶偺掕棟傛傝丄俁捈慄俙俢乫丄俛俤乫丄俠俥乫偑侾揰偱岎傢傞偙偲傪
堄枴偡傞丅丂丂乮暿徹廔乯
乮僐儊儞僩乯丂婎杮揑偵俀偮偺徹柧偼丄傎偲傫偳摨媊偱偁傞丅
乮墳梡椺乯丂嶰妏宍俙俛俠偺悅怱俫偲奜怱俷偼丄屳偄偵摍妏嫟栶揰偱偁傞丅
乮徹柧乯丂壓恾偵偍偄偰丄
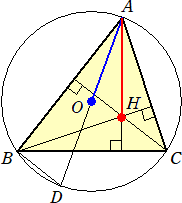 |
丂丂佢俠俙俫亖俋侽亱亅佢俠
丂丂佢俠亖佢俢丂丄佢俙俛俢亖俋侽亱丂側偺偱丄
丂丂佢俷俙俛亖俋侽亱亅佢俢亖俋侽亱亅佢俠
丂傛偭偰丄佢俠俙俫亖佢俷俙俛丂偲側傝丄佢俙偺俀摍暘慄偵娭偟偰丄
丂俙俫偲俙俷偼懳徧偱偁傞丅丂 |
丂摨條偵丄佢俛偺俀摍暘慄偵娭偟偰丄俛俫偲俛俷偼懳徧偱丄佢俠偺俀摍暘慄偵娭偟偰丄俠俫偲俠俷
偼懳徧偲側傞丅埲忋偐傜丄悅怱俫偲奜怱俷偼摍妏嫟栶揰偱偁傞丅丂丂乮徹廔乯
乮曗懌乯丂丒撪怱偺摍妏嫟栶揰偼撪怱帺恎偱偁傞丅
丂丂丂丂丂丒朤怱偺摍妏嫟栶揰偼朤怱帺恎偱偁傞丅
乮慜採抦幆偦偺俀乯丂摍嫍棧嫟栶揰 (isotomic conjugate)
丂嶰妏宍ABC偺奺曈偍傛傃偦偺墑挿慄偺忋偵側偄揰P傪偲傞丅捈慄AP偲BC偺岎揰傪L丄BP
偲CA偺岎揰傪M丄CP偲AB偺岎揰傪N偲偟丄
丂慄暘BC偺拞揰偵娭偟偰揰俴偲懳徧側揰傪俴乫
丂慄暘CA偺拞揰偵娭偟偰揰俵偲懳徧側揰傪俵乫
丂慄暘AB偺拞揰偵娭偟偰揰俶偲懳徧側揰傪俶乫
偲偡傞偲丄俁杮偺捈慄A俴乫丄B俵乫丄C俶乫偼侾揰俻偱岎傢傞丅偙偺岎揰傪(嶰妏宍ABC偵娭偡傞)
揰P偺摍嫍棧嫟栶揰偲偄偆丅
丂丂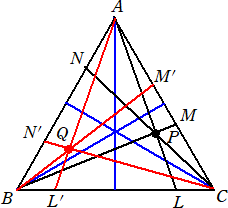
丂乽俁杮偺捈慄俙俴乫丄俛俵乫丄俠俶乫偑侾揰俻偱岎傢傞乿偙偲偼丄師偺傛偆偵丄僠僃僶偺掕棟傪
梡偄偰帵偝傟傞丅
乮徹柧乯丂俁捈慄俙俴丄俛俵丄俠俶偑侾揰偱岎傢傞偺偱丄僠僃僶偺掕棟偵傛傝丄
丂乮俙俶/俶俛乯丒乮俛俴/俴俠乯丒乮俠俵/俵俙乯亖侾丂偑惉傝棫偮丅
丂戣堄傛傝丄丂俙俶亖俛俶乫丄俛俶亖俙俶乫丄俛俴亖俠俴乫丄俠俴亖俛俴乫丄俠俵亖俙俵乫丄俙俵亖俠俵乫
側偺偱丄丂乮俛俶乫/俶乫俙乯丒乮俠俴乫/俴乫俛乯丒乮俙俵乫/俵乫俠乯亖侾丂偡側傢偪丄
丂乮俛俶乫/俶乫俙乯丒乮俙俵乫/俵乫俠乯丒乮俠俴乫/俴乫俛乯亖侾丂偑惉傝棫偮丅
傛偭偰丄僠僃僶偺掕棟傛傝丄俁捈慄俙俴乫丄俛俵乫丄俠俶乫偼侾揰俻偱岎傢傞丅丂丂乮徹廔乯
丂偦傟偱偼丄栤戣偱偡丅
栤戣偦偺侾
丂嶰妏宍偺撪愙墌偵懳偟偰丄偁傞傂偲偮偺朤怱偐傜俀杮偺愙慄傪堷偄偨偲偒偺俀偮偺愙揰偼
屳偄偵摍妏嫟栶揰偱偁傞偙偲傪帵偣丅
栤戣偦偺俀
丂嶰妏宍ABC偵懳偟偰丄巐妏宍ABCD偑暯峴巐曈宍偲側傞傛偆偵揰D傪偲傞丅嶰妏宍ABC偺
撪愙墌偵懳偟偰丄揰D偐傜俀杮偺愙慄傪堷偄偨偲偒偺俀偮偺愙揰偼丄屳偄偵摍嫍棧嫟栶揰
偱偁傞偙偲傪帵偣丅
丂夡傟偨斷偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俆擭俇寧侾侽擔晅偗乯
丂栤戣偦偺侾偵偮偄偰丄偪傚偭偲峫偊偰傒傑偟偨丅
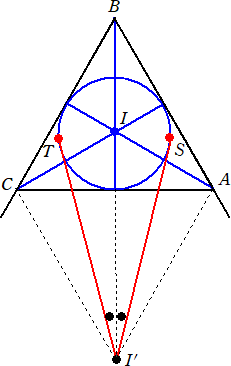 |
乮夝乯丂仮俙俛俠偺撪怱傪 俬 偲偟丄佢俛撪偺朤怱傪 俬乫偲偡
丂傞偲丄俁揰俛丄俬丄俬乫偼堦捈慄忋偵偁傝丄俬乫偐傜撪愙墌偵
丂堷偄偨愙慄偺俀偮偺愙揰傪 俬乫俬 偵娭偟偰揰俙懁傪俽丄
丂揰俠懁傪俿偲偡傞偲丄俙俬 偼佢俙偺擇摍暘慄偱丄俙俬乫偼
丂佢俙偺奜妏偺擇摍暘慄傛傝丄佢俬俙俬乫亖俋侽亱
丂傑偨丄俬乫俽佦俬俽 傛傝丄佢俬俽俬乫亖俋侽亱
丂傛偭偰丄佢俬俙俬乫亖佢俬俽俬乫傛傝丄墌廃妏偺掕棟偺媡偵傛傝丄
丂係揰俽丄俬丄俬乫丄俙偼摨堦墌廃忋偵偁傞丅
丂偲偙傠偱丄仮俬乫俽俬佭仮俬乫俿俬 傛傝丄佢俽俬乫俬亖佢俿俬乫俬亖仠 |
丂偲抲偔偲丄墌廃妏傛傝丄佢俽俙俬亖佢俽俬乫俬亖仠丂偱偁傞丅
丂傑偨丄佢俬俿俬乫亖俋侽亱丄佢俬俙俬乫亖俋侽亱傛傝丄巐妏宍俙俬俿俬乫偼墌偵撪愙偡傞巐妏宍偱偁傞丅
傛偭偰丄墌廃妏傛傝丄佢俬俙俿亖佢俬俬乫俿亖仠丂偐傜丄佢俽俙俬亖佢俬俙俿
偲偙傠偱丄俙俬偼佢俙偺擇摍暘慄傛傝丄俙俽偲俙俿偼丄佢俙偺擇摍暘慄偵娭偟偰嬀塮偱偁傞丅
傑偨丄仮俬乫俽俬佭仮俬乫俿俬 傛傝丄佢俬乫俬俽亖佢俬乫俬俿丂側偺偱丄佢俛俬俽亖佢俛俬俿
傑偨丄敿宎傛傝丄俬俽亖俬俿丂偱丄俛俬 偼嫟捠傛傝丄擇曈汃妏偑摍偟偄偺偱丄仮俛俬俽佭仮俛俬俿
傛傝丄佢俬俛俽亖佢俬俛俿丂偱偁傞丅
偲偙傠偱丄俛俬偼佢俛偺擇摍暘慄傛傝丄俛俽偲俛俿偼佢俛偺擇摍暘慄偵娭偟偰嬀塮偱偁傞丅
傛偭偰丄揰俽偲揰俿偼屳偄偵摍妏嫟栶揰偱偁傞丅傛偭偰丄帵偝傟偨丅
乮曗懌乯
佢俬俿俬乫亖佢俬俠俬乫亖俋侽亱偐傜丄係揰 俬丄俿丄俠丄俬乫偼摨堦墌廃忋偵偁傝丄墌廃妏傛傝丄
佢俿俠俬亖佢俿俬乫俬亖仠丂偱偁傞丅
傑偨丄巐妏宍俽俬俠俬乫偼丄墌偵撪愙偡傞巐妏宍傛傝丄墌廃妏偱丄佢俬俠俽亖佢俬俬乫俽亖仠
傛傝丄佢俿俠俬亖佢俬俠俽丂偱偁傞丅
偲偙傠偱丄俠俬偼佢俠偺擇摍暘慄傛傝丄俠俿偲俠俽偼佢俠偺擇摍暘慄偵娭偟偰嬀塮偱偁傞丅丂乮廔乯
乮僐儊儞僩乯丂夡傟偨斷偝傫丄徹柧傪偁傝偑偲偆偛偞偄傑偡丅旤偟偄徹柧偱偡偹両
丂傝傜傂偄偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俆擭俇寧侾俀擔晅偗乯
丂夡傟偨斷偝傫丄摎偊偰偄偨偩偒偁傝偑偲偆偛偞偄傑偡丅俇偮偺揰 A丄C丄S丄T丄I丄I乫 偑摨堦墌
廃忋偵偁傞傫偱偡偹丅
丂栤戣偦偺侾偼丄偦傟傎偳擄偟偔偼側偄偩傠偆側偲側傫偲側偔巚偭偰偄傑偟偨偑丄偐側傝偒傟偄
側宍偱偟偨丅
丂偪側傒偵丄
丂乽嶰妏宍偺朤愙墌偵懳偟偰撪怱偐傜俀杮偺愙慄傪堷偄偨偲偒偺俀偮偺愙揰偼屳偄偵摍妏
嫟栶揰偱偁傞乿
偙偲傕傎偲傫偳摨條偵帵偣傑偡丅
丂丂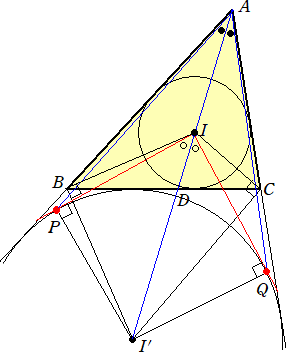
丂夡傟偨斷偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俆擭俇寧侾係擔晅偗乯
丂傝傜傂偄偝傫偺
丂乽嶰妏宍偺朤愙墌偵懳偟偰撪怱偐傜俀杮偺愙慄傪堷偄偨偲偒偺俀偮偺愙揰偼屳偄偵摍妏
嫟栶揰偱偁傞乿
偙偲傕傎偲傫偳摨條偵帵偣傑偡丅
丂愭掱傗偭偰傒傑偟偨丅乽傎偲傫偳摨條乿偺堄枴偑暘偐傝傑偟偨丅偁傞撲傪夝偐側偄偲偄偗傑
偣傫偹丅
乮僐儊儞僩乯丂忋婰偺徹柧偵挧愴偟偰傒傑偟偨丅乮椷榓俆擭俇寧俀侽擔晅偗乯
乮徹柧乯丂忋恾偺仮俙俹俬 偲仮俙俻俬 偵偍偄偰丄俙俬 偼嫟捠丄俬俹亖俬俻丄佢俙俬俹亖佢俙俬俻丂偐傜丄
仮俙俹俬 佭仮俙俻俬 側偺偱丄丂佢俹俙俬 亖佢俻俙俬
傛偭偰丄俙俹丄俙俻偼俙俬 偵娭偟偰嬀塮偱偁傞丅
丂傑偨丄俇揰 俬丄俛丄俹丄俬乫丄俻丄俠偼摨堦墌廃忋偵偁傞偺偱丄俹俬乫亖俻俬乫偐傜丄
丂佢俹俛俬乫亖佢俻俛俬乫丂偲側傞偺偱丄俛俹丄俛俻偼俛俬乫偵娭偟偰嬀塮偱偁傞丅
摨條偵偟偰丄丂佢俹俠俬乫亖佢俻俠俬乫丂偲側傞偺偱丄俠俹丄俠俻偼俠俬乫偵娭偟偰嬀塮偱偁傞丅
丂埲忋偐傜丄俹丄俻偼屳偄偵摍妏嫟栶揰偲側傞丅丂丂乮徹廔乯
丂栤戣偦偺俀傪夝偙偆偲偡傞曽偺偨傔偵丄恾偺弨旛傪偟偰偍偙偆丅
丂嶰妏宍ABC偺撪愙墌偺拞怱傪 俬 偲偟偰丄揰D偐傜撪愙墌偵堷偄偨愙慄偺愙揰傪俹丄俻偲偍
偔丅曈俛俠丄俠俙丄俙俛偺拞揰傪偦傟偧傟俙乫丄俛乫丄俠乫偲偍偔丅偙偺偲偒丄捈慄俙俹丄俙俻偑曈俛俠偲
岎傢傞揰傪偦傟偧傟俴丄俴乫偲偍偔丅摨條偵丄捈慄俛俹丄俛俻偑曈俠俙偲岎傢傞揰傪偦傟偧傟俵丄
俵乫偲偍偒丄捈慄俠俹丄俠俻偑曈俙俛偲岎傢傞揰傪偦傟偧傟俶丄俶乫偲偍偔丅
丂俀揰俹丄俻偑摍嫍棧嫟栶揰偱偁傞偙偲傪帵偡偵偼丄
丂俴俙乫亖俴乫俙乫丂丄俵俛乫亖俵乫俛乫丂丄俶俠乫亖俶乫俠乫
傪帵偣偽傛偄丅
丂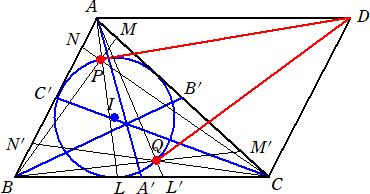
丂傝傜傂偄偝傫偐傜怴偟偄栤戣偑撏偒傑偟偨丅乮椷榓俆擭俇寧侾係擔晅偗乯
丂忋婰偺榖戣偵娭楢偟偰丄傕偆堦栤搳峞偟偰傒傑偡丅偙偪傜傕栤戣偼嶌傝傑偟偨偑丄帺暘偱夝
偄偰偼偄側偄偺偱丄夝摎偼梡堄偟偰偄傑偣傫丅
乮偙偺栤戣偺撪梕傪娷傓傛傝堦斒揑側柦戣偑惉傝棫偮偙偲偼妋擣偟偰偄傑偡丅乯
栤戣偦偺俁
丂嶰妏宍ABC偑偁傝丄慄暘BC偺拞揰傪D丄慄暘CA偺拞揰傪E丄慄暘AB偺拞揰傪F偲偡傞丅嶰
妏宍ABC偺奜愙墌俷偲捈慄EF偺俀偮偺岎揰俽丄俿偵偍偗傞奜愙墌偺愙慄傪俴丄俴乫偲偡傞丅捈
慄俴偲捈慄BC丄CA丄AB 偺岎揰傪偦傟偧傟 P丄Q丄R 偲偟丄捈慄俴乫偲捈慄BC丄CA丄AB 偺岎揰
傪偦傟偧傟P乫丄俻乫丄俼乫偲偡傞丅偙偺偲偒丄 PD亖DP乫丂丄QE亖EQ乫丂丄RF亖FR乫 偑惉傝棫偮偙
偲傪帵偣丅
丂丂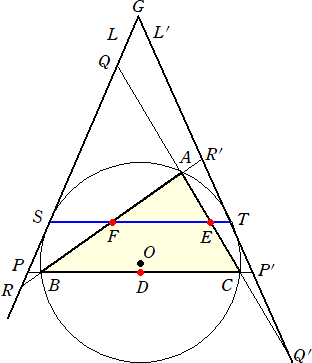
丂夡傟偨斷偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俆擭俇寧侾係擔晅偗乯
丂傝傜傂偄偝傫丄娙扨側傗偮侾偮偩偗偱傕傛傠偟偄偱偟傚偆偐丅
乮鶣乯丂PD亖DP乫 偺徹柧
丂戣堄傛傝丄俀揰俤丄俥偼慄暘俽俿忋偵偁傝丄仮俙俛俠偱偺拞揰楢寢掕棟傛傝丄俥俤//俛俠
偡側傢偪丄俽俿//俛俠丂偱偁傞丅
傑偨丄捈慄俴偲俴乫偺岎揰傪俧偲偡傞偲丄墌偲愙慄偺娭學傛傝丄俧俽亖俧俿丂偐傜丄仮俧俽俿偼擇摍
曈嶰妏宍偱偁傞丅
傑偨丄揰俹丄俹乫偼俛俠偺墑挿忋偵偁傝丄俽俿//俛俠傛傝丄俽俿//俹俹乫 偱偁傞丅
丂傛偭偰丄仮俧俽俿佷仮俧俹俹乫丂傛傝丄仮俧俹俹'傕擇摍曈嶰妏宍偱偁傞丅
丂傛偭偰丄俧偐傜俹俹乫偵悅慄傪壓傠偟丄偦偺懌傪俫偲偡傞偲丄俹俫亖俫俹乫丂丒丒丒丂嘆
偲偙傠偱丄俽俿//俛俠 傛傝丄巐妏宍俽俛俠俿偼戜宍偱丄墌偵撪愙偡傞戜宍偼摍媟戜宍偱丄傑偨丄
仮俧俽俿偼擇摍曈嶰妏宍傛傝丄揰俫偼丄俛俠偺拞揰偱偁傞丅偡側傢偪丄俫亖俢丂丒丒丒丂嘇
丂嘇傪嘆偵戙擖偡傞偲丄俹俢亖俢俹乫丂側偺偱丄傛偭偰丄帵偝傟偨丅丂丂乮徹廔乯
乮曗懌乯丂墌偵撪愙偡傞戜宍偼摍媟戜宍偱偁傞帠傪巊傢側偄応崌偼丄俛俿傪寢傇偲嶖妏傛傝丄
丂佢俽俿俛亖佢俿俛俠丂傛傝丄屖俽俛亖屖俿俠丂側偺偱丄俽俛亖俿俠
丂傑偨丄俽俿//俛俠 傛傝丄巐妏宍俽俛俠俿偼摍媟戜宍偱偁傞丅
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俆擭俇寧侾係擔晅偗乯
丂偙偺柦戣偵偼丄佢B 偲 佢C 偑捈妏偱偼側偄偲偄偆慜採偑昁梫側婥偑偟傑偡丅偁傞偄偼丄暯
峴慄偼柍尷墦偱岎傢偭偰偄傞偲傒側偡偲曗懌傪擖傟傞偐丅偦傟偼偦傟偲偟偰丄PD = DP乫 偵
偮偄偰偼丄曈 BC 偺悅捈擇摍暘慄傪堷偔偲丄俴偲俴乫偑偙偺捈慄偵娭偟偰懳徧偵側傞丄偲偄偆偙
偲傪峫偊傟偽丄傢傝偲帺柧側姶偠偑偟傑偡偹丅
丂傝傜傂偄偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俆擭俇寧侾俆擔晅偗乯
丂妋偐偵偦偆偱偡偹丅幐楃偟傑偟偨丅佢B 偲 佢C 偑捈妏偱偼側偄偲偡傞偺偑傛偝偦偆偱偡偹丅
乮暯峴慄偼柍尷墦偱岎傢偭偰偄傞偲傒側偡偲曗懌傪擖傟傞応崌偼丄岎揰偼掕媊偝傟偰傕挿偝
偑掕媊偝傟側偄偺偱丄栤戣暥偺嵟屻傪乽P偲P'偑D偵娭偟偰懳徧乿偺傛偆側宍偵偡傞偺偑傛偄
偱偡偐偹丠懳徧偺掕媊偑柍尷墦揰偵媦傇偐傢偐傜側偄偐傜旝柇偐側丠乯
丂乽摍妏嫟栶揰偲摍嫍棧嫟栶揰乿偺巹偺愢柧傕丄暯峴慄偲側傞応崌偑敳偗偰偄偰晄廫暘偱偡
偹丅儐乕僋儕僢僪暯柺偵柍尷墦揰偺廤崌偱偁傞柍尷墦捈慄傪壛偊偰幩塭暯柺偺掕媊傪枮偨
偡傛偆偵奼挘偟偨暯柺偱峫偊偰偄傞偲偟偰偔偩偝偄丅偙偺奼戝儐乕僋儕僢僪暯柺偱偼暯峴慄偼
柍尷墦揰偱岎傢傝傑偡丅
丂傝傜傂偄偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俆擭俇寧侾俆擔晅偗乯
丂傕偆堦栤嶌傝傑偟偨丅椺偺偛偲偔丄栤戣偼嶌傝傑偟偨偑帺暘偱夝偄偰偼偄側偄偺偱丄夝摎偼
梡堄偟偰偄傑偣傫丅
乮偙偺栤戣偺撪梕傪娷傓傛傝堦斒揑側柦戣偑惉傝棫偮偙偲偼妋擣偟偰偄傑偡丅乯
栤戣偦偺係
丂嶰妏宍ABC偑偁傝丄佢A偺擇摍暘慄偲曈BC偺岎揰傪D丄佢B偺擇摍暘慄偲曈CA偺岎揰傪
E丄佢C偺擇摍暘慄偲曈AB偺岎揰傪F偲偡傞丅撪怱傪 俬 偲偍偔丅嶰妏宍ABC偺奜愙墌偲捈慄
EF偺俀偮偺岎揰俽丄俿偵偍偗傞奜愙墌偺愙慄傪俴丄俴乫偲偡傞丅俴偲俴乫偺岎揰傪俧偲偍偔丅捈慄俴
偲捈慄BC丄CA丄AB偺岎揰傪偦傟偧傟 P丄Q丄R 偲偟丄捈慄俴乫偲捈慄BC丄CA丄AB偺岎揰傪偦
傟偧傟P乫丄Q乫丄R乫偲偡傞丅偙偺偲偒丄佢PAD=佢DAP乫丂丄佢QBE=佢EBQ乫丂丄佢RCF=佢FCR乫
偑惉傝棫偮偙偲傪帵偣丅
丂丂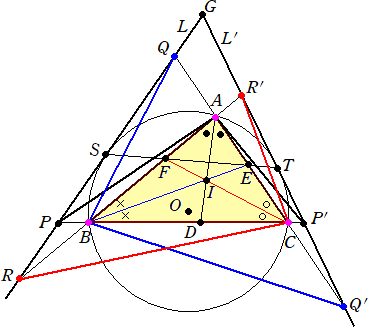
#GeoGebra偱嶌恾偟偰傒傞偲丄偳偆傗傜 佢QBE(=佢EBQ乫) 偲 佢RCF(=佢FCR乫) 傕摍偟偔側傝
偦偆偱偡丅偙偪傜偼徹柧偟偰偄側偄偺偱惓偟偄偐偳偆偐傢偐傝傑偣傫丅
丂傝傜傂偄偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俆擭俇寧俀俀擔晅偗乯
丂偙偺栤戣偺尦僱僞乮傛傝堦斒揑側柦戣乯傪嵹偣偰偍偒傑偡丅
丂埲壓丄儐乕僋儕僢僪暯柺偵柍尷墦揰偺廤崌偱偁傞柍尷墦捈慄傪壛偊偰丄幩塭暯柺偺掕媊
傪枮偨偡傛偆偵奼挘偟偨暯柺偱峫偊傑偡丅偙偺奼戝儐乕僋儕僢僪暯柺偱偼丄擟堄偺堎側傞俀揰
傪寢傇捈慄偑偨偩侾偮懚嵼偟丄擟堄偺堎側傞俀捈慄偼偨偩侾揰偱岎傢傝傑偡丅
亙偙偲偽偺掕媊亜丂撪愙擇師嬋慄
丂俁捈慄BC丄CA丄AB偵愙偡傞擇師嬋慄傪嶰妏宍ABC偺撪愙擇師嬋慄偲偄偆丅
仸嶰妏宍偺撪懁偵偁傝丄俁曈偵愙偡傞懭墌偩偗偱偼側偔丄嶰妏宍偺奜懁偵偁傝丄侾曈偲巆傝俀
丂曈偺墑挿慄偵愙偡傞懭墌丒曻暔慄丒憃嬋慄傪娷傔傞丅
栤戣偦偺侾偺尦僱僞
丂嶰妏宍ABC偺撪怱偲俁偮偺朤怱偺拞偐傜嶰妏宍ABC偺撪愙擇師嬋慄儭偵俀杮偺愙慄偑
堷偗傞揰傪慖傇丅偦偺揰偐傜儭偵堷偄偨俀杮偺愙慄偺愙揰偼丄屳偄偵嶰妏宍ABC偵娭偡傞
摍妏嫟栶揰偱偁傞丅
栤戣偦偺俀偺尦僱僞
丂嶰妏宍ABC偵懳偟偰丄巐妏宍ABA乫C丄ABCB乫丄AC乫BC 偑暯峴巐曈宍偲側傞傛偆偵揰A乫丄
B乫丄C乫傪掕傔傞丅嶰妏宍ABC偺廳怱G偲俁揰A乫丄B乫丄C乫偺拞偐傜嶰妏宍ABC偺撪愙擇師
嬋慄儭偵俀杮偺愙慄偑堷偗傞揰傪慖傇丅偦偺揰偐傜儭偵堷偄偨俀杮偺愙慄偺愙揰偼屳偄
偵嶰妏宍ABC偵娭偡傞摍嫍棧嫟栶揰偱偁傞丅
丂尦僱僞偺尦僱僞乮傛傝堦斒揑側柦戣乯傕嵹偣偰偍偒傑偡丅
丂摍妏嫟栶揰傗摍嫍棧嫟栶揰偼丄偝傜偵堦斒壔偝傟偨乽揰偺嫟栶娭學乿偺偆偪偺傂偲偮偱
偡丅堦斒壔偝傟偨揰偵娭偡傞嫟栶娭學偵偼丄帺屓嫟栶側揰傪係偮帩偮傕偺偲侾偮傕帩偨側偄
傕偺偑偁傝傑偡丅
丂尦僱僞偺尦僱僞
丂嶰妏宍ABC偵娭偟偰丄帺屓嫟栶側揰傪係偮帩偮乽揰偵娭偡傞嫟栶娭學乿傪傂偲偮寛傔傞丅
偦偺係偮偺帺屓嫟栶側揰偺拞偐傜嶰妏宍ABC偺撪愙擇師嬋慄儭偵俀杮偺愙慄偑堷偗傞揰
傪慖傇丅偦偺揰偐傜儭偵堷偄偨俀杮偺愙慄偺愙揰偼屳偄偵嵟弶偵掕傔偨嫟栶娭學偵偁傞丅
丂偙偺尦僱僞偺尦僱僞偼丄幩塭婔壗偺斖醗側偺偱丄憃懳偑惉傝棫偪傑偡丅偦偺憃懳偑丄傕偆
傂偲偮偺乽嶰妏宍偺奜愙擇師嬋慄偲嫟栶捈慄乿偺尦僱僞偺尦僱僞偵側傝傑偡丅
乮慜採抦幆偦偺俁乯丂憡斀嫟栶慄
丂嶰妏宍ABC偺奺捀揰傪捠傜側偄捈慄俴傪偲傞丅捈慄俴偲捈慄BC丄CA丄AB偺岎揰傪偦傟偧
傟P丄Q丄R 偲偟丄慄暘BC偺拞揰偵娭偟偰揰P偲懳徧側揰傪P乫丄慄暘CA偺拞揰偵娭偟偰揰Q偲
懳徧側揰傪Q乫丄慄暘AB偺拞揰偵娭偟偰揰R偲懳徧側揰傪R乫偲偡傞偲丄俁揰P乫丄Q乫丄R乫偼堦捈
慄忋偵偁傞丅偙偺捈慄傪(嶰妏宍ABC偵娭偡傞)捈慄l偺憡斀嫟栶慄偲偄偆丅
乮慜採抦幆偦偺係乯丂妏搙偺嫟栶慄丠
丂嶰妏宍ABC偺奺捀揰傪捠傜側偄捈慄俴傪偲傞丅捈慄俴偲捈慄BC丄CA丄AB 偺岎揰傪偦傟偧
傟P丄Q丄R 偲偟丄妏A偺擇摍暘慄偵娭偡傞捈慄AP偺嬀塮偑捈慄BC偲岎傢傞揰傪P乫丄妏B偺
擇摍暘慄偵娭偡傞捈慄BP偺嬀塮偑捈慄CA偲岎傢傞揰傪Q乫丄妏C偺擇摍暘慄偵娭偡傞捈
慄CP偺嬀塮偑捈慄AB偲岎傢傞揰傪R乫偲偡傞偲丄俁揰P乫丄Q乫丄R乫偼堦捈慄忋偵偁傞丅
丂偙偺捈慄傪壗偲偄偆偺偐傢偨偟偼抦傝傑偣傫偟丄偦傕偦傕柤徧偑偁傞偺偐偳偆偐傕傢偐傝傑
偣傫偺偱丄偙偱偼丄偙偺捈慄傪(嶰妏宍ABC偵娭偡傞)捈慄俴偺妏搙偺嫟栶慄偲屇傇偙偲偵
偟傑偡丅
亙偙偲偽偺掕媊亜丂奜愙擇師嬋慄
丂俁揰A丄B丄C傪捠傞擇師嬋慄傪嶰妏宍ABC偺奜愙擇師嬋慄偲偄偆丅
仸堦晹偑嶰妏宍ABC偺撪晹傪捠傞憃嬋慄傕娷傔傞丅
亙偙偲偽偺掕媊亜丂antiorthic axis
丂嶰妏宍ABC偵懳偟偰丄揰A丄B丄C偺奜妏偺擇摍暘慄偲懳曈偺墑挿慄偺岎揰傪偦傟偧傟
D乫丄E乫丄F乫偲偡傞偲丄偙偺俁揰偼堦捈慄忋偵偁傞丅偙偺捈慄傪嶰妏宍ABC偺 antiorthic axis
偲偄偆丅(擔杮岅偺柤徧偼傢偐傝傑偣傫丅)
栤戣偦偺俁偺尦僱僞
丂嶰妏宍ABC偑偁傝丄慄暘BC偺拞揰傪D丄慄暘CA偺拞揰傪E丄慄暘AB偺拞揰傪F偲偡傞丅柍
尷墦捈慄偲捈慄EF丄FD丄DE偺拞偐傜嶰妏宍ABC偺奜愙擇師嬋慄儭偲俀揰偱岎傢傞捈慄傪
慖傇丅偦偺捈慄偲儭偺俀偮偺岎揰偵偍偗傞愙慄偼屳偄偵嶰妏宍ABC偵娭偡傞憡斀嫟栶慄偱
偁傞丅
栤戣偦偺係偺尦僱僞
丂嶰妏宍ABC偑偁傝丄揰A丄B丄C偺撪妏偺擇摍暘慄偲懳曈偺岎揰傪偦傟偧傟D丄E丄F偲偡傞丅
嶰妏宍ABC偺 antiorthic axis 偲捈慄EF丄FD丄DE偺拞偐傜嶰妏宍ABC偺奜愙擇師嬋慄儭偲
俀揰偱岎傢傞捈慄傪慖傇丅偦偺捈慄偲儭偺俀偮偺岎揰偵偍偗傞愙慄偼屳偄偵嶰妏宍ABC偵
娭偡傞妏搙偺嫟栶慄偱偁傞丅
丂尦僱僞偺尦僱僞乮傛傝堦斒揑側柦戣乯傕嵹偣偰偍偒傑偡丅
丂憡斀嫟栶慄傗妏搙偺嫟栶慄偼丄偝傜偵堦斒壔偝傟偨乽捈慄偺嫟栶娭學乿偺偆偪偺傂偲偮偱
偡丅堦斒壔偝傟偨捈慄偵娭偡傞嫟栶娭學偵偼丄帺屓嫟栶側捈慄傪係偮帩偮傕偺偲侾偮傕帩偨
側偄傕偺偑偁傝傑偡丅
尦僱僞偺尦僱僞
丂嶰妏宍ABC偵娭偟偰丄帺屓嫟栶側捈慄傪係偮帩偮乽捈慄偵娭偡傞嫟栶娭學乿傪傂偲偮寛傔
傞丅偦偺係偮偺帺屓嫟栶側捈慄偺拞偐傜嶰妏宍ABC偺奜愙擇師嬋慄儭偲俀揰偱岎傢傞捈慄
傪慖傇丅偦偺捈慄偲儭偺俀偮偺岎揰偵偍偗傞愙慄偼屳偄偵嵟弶偵掕傔偨嫟栶娭學偵偁傞丅
丂偙偺尦僱僞偺尦僱僞偼丄幩塭婔壗偺斖醗側偺偱憃懳偑惉傝棫偪傑偡丅偦偺憃懳偑傕偆傂偲
偮偺乽嶰妏宍偺撪愙擇師嬋慄偲嫟栶揰乿偺尦僱僞偺尦僱僞偵側傝傑偡丅
丂傢偨偟偑偙傟傜偺偙偲傪峫偊傞偒偭偐偗偵側偭偨偺偼丄師偺掕棟傪尒偐偗偨偙偲偵傛傝傑偡丅
丂栤戣偦偺侾偐傜偦偺係傗偦傟傜偺尦僱僞偺柦戣偼師偺掕棟偐傜偺楢憐偱惗傑傟傑偟偨丅
丂嶰妏宍ABC偺憡斀嫟栶慄偲側傞俀捈慄偺慻偼丄俁揰A丄B丄C傪捠傞偁傞憃嬋慄偺
俀杮偺慟嬤慄偱偁傞丅
乮僐儊儞僩乯丂宖帵斅乽弌夛偄偺愹乿偵偍偗傞僞僀僩儖乽嶰妏宍偺亀撪愙擇師嬋慄亁傗嶰妏宍偺
丂丂丂丂丂丂亀奜愙擇師嬋慄亁偵丄偳傫側娭學偑偁傞偺偐晄巚媍偱偟偨偑丄傝傜傂偄偝傫偺庬柧
丂丂丂丂丂丂偐偟傪巉偭偰丄崌揰偑偄偒傑偟偨丅
丂捈妏憃嬋慄 倷亖侾/倶 忋偵俁揰俙乮侾丆侾乯丄俛乮俀丆侾/俀乯丄俠乮亅侾丆亅侾乯傪偲傞丅
捈慄俛俠偺曽掱幃偼丄丂倷亖乮侾/俀乯倶亅侾/俀丂側偺偱丄揰俙偐傜俛俠偵壓傠偟偨悅慄偺曽掱幃偼丄
丂倷亖亅俀倶亄俁丂偱偁傞丅摨條偵偟偰丄丂捈慄俠俙偺曽掱幃偼丄倷亖倶丂側偺偱丄揰俛偐傜俠俙偵壓
傠偟偨悅慄偺曽掱幃偼丄丂倷亖亅倶亄俆/俀丂偱偁傞丅丂偟偨偑偭偰丄仮俙俛俠偺悅怱俫偺嵗昗偼丄
乮侾/俀丆俀乯偲側傝丄俫偼丄柧傜偐偵丄捈妏憃嬋慄 倷亖侾/倶 忋偺揰偱偁傞丅
丂丂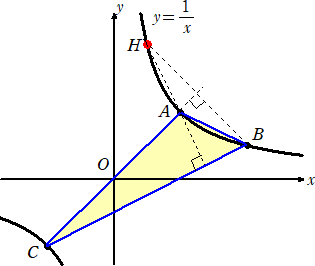
丂媡偵丄嶰妏宍偺捀揰偲悅怱傪捠傞憃嬋慄偼捈妏憃嬋慄偱偁傞偙偲偑抦傜傟偰偄傞丅
丂偙偺偲偒丄捈妏憃嬋慄 倷亖侾/倶 偼丄仮俙俛俠偺奜愙擇師嬋慄偲尵傢傟傞丅
丂師偺掕棟偑抦傜傟偰偄傞丅
掕棟丂丂仮俙俛俠偵偍偄偰丄摍妏嫟栶揰傪俹丄俻偲偡傞丅偙偺偲偒丄偙偺俀揰傪徟揰偲偟丄仮俙俛俠
丂丂丂丂偺俁曈偵撪愙偡傞俀師嬋慄乮仮俙俛俠偺撪愙擇師嬋慄乯偑懚嵼偡傞丅
乮曗懌乯丂丒俹丄俻偑偲傕偵仮俙俛俠偺撪晹丄傑偨偼丄奜愙墌偺奜晹偵偁傞偲偒丄俀師嬋慄偼懭墌
丂丂丂丂丒俹丄俻偺堦曽偑仮俙俛俠偺奜晹偐偮奜愙墌偺撪晹偵偁傝丄懠曽偑奜愙墌偺奜晹偵偁傞
丂丂丂丂偲偒丄俀師嬋慄偼憃嬋慄
丂丂丂丂丒俹丄俻偺堦曽偑仮俙俛俠偺奜愙墌忋乮捀揰偼彍偔乯偵偁傝丄懠曽偑柍尷墦揰偱偁傞偲偒丄
丂丂丂丂俀師嬋慄偼曻暔慄
掕棟丂丂仮俙俛俠偵偍偄偰丄摍妏嫟栶揰傪俹丄俻偲偡傞丅俹傛傝丄俁曈偵悅慄偺懌俹1丄俹2丄俹3傪
丂丂丂丂壓偡丅摨條偵丄俻傛傝丄俁曈偵悅慄偺懌俻1丄俻2丄俻3傪壓偡丅
丂丂丂丂偙偺偲偒丄俇揰俹1丄俹2丄俹3丄俻1丄俻2丄俻3偼摨堦墌廃忋偵偁傝丄慄暘俹俻偺拞揰偑墌
丂丂丂丂偺拞怱偲側傞丅
丂丂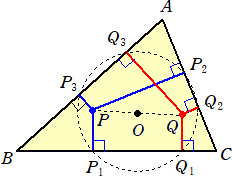
乮徹柧乯丂墌偼俁揰偱掕傑傞偺偱丄係揰俹1丄俹3丄俻1丄俻3 偑摨堦墌廃忋偵偁傞偙偲傪帵偣偽
丂丂丂丂廫暘偱偁傞丅
丂丂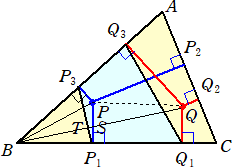
丂係揰俛丄俹1丄俹丄俹3 偼摨堦墌廃忋偵偁傞偺偱丄丂佢俹俹1俹3亖佢俹俛俹3
丂俹丄俻偼摍妏嫟栶揰側偺偱丄丂佢俹俛俹3亖佢俻俛俻1
丂係揰俛丄俻1丄俻丄俻3 偼摨堦墌廃忋偵偁傞偺偱丄丂佢俻俛俻1亖佢俻俻3俻1
丂傛偭偰丄丂佢俹俹1俹3亖佢俻俻3俻1丂偱偁傞丅偙偺偲偒丄
丂佢俻1俹1俹3亖佢Q1俹1俹亄佢俹俹1俹3亖俋侽亱亄佢俹俹1俹3亖俋侽亱亄佢俻俻3俻1
丂亖佢俻俻3俙亄佢俻俻3俻1亖佢俙俻3俻1
偑惉傝棫偮偺偱丄係揰俹1丄俹3丄俻1丄俻3 偼摨堦墌廃忋偵偁傞丅
丂摨條偵偟偰丄係揰俹1丄俹2丄俹3丄俻3 傕摨堦墌廃忋偵偁傝丄係揰俹1丄俹3丄俻1丄俻2 傕摨堦墌
廃忋偵偁傞偙偲偐傜丄寢嬊丄俇揰俹1丄俹2丄俹3丄俻1丄俻2丄俻3偼摨堦墌廃忋偵偁傞丅
墌偺拞怱偼丄慄暘俹1俻1偲慄暘俹3俻3 偺悅捈俀摍暘慄偺岎揰偱丄慄暘俹俻偺拞揰偱岎傢傞丅
偡側傢偪丄墌偺拞怱偼丄慄暘俹俻偺拞揰偱偁傞丅丂丂乮徹廔乯
乮僐儊儞僩乯丂忋婰偺徹柧偵偼捈愙娭學偟側偄偑丄乽俛俻佦俹1俹3乿偲偄偆娭學偑惉傝棫偮偙偲偵丄
丂丂丂丂丂丂忋婰偺徹柧傪峫嶡偟偰偄傞嵺偵婥偑晅偄偨丅
丂幚嵺偵丄仮俽俛俹1偲仮俽俹1俿偵偍偄偰丄係揰俛丄俹1丄俹丄俹3 偼摨堦墌廃忋偵偁傞偺偱丄
丂佢俹俹1俹3亖佢俹俛俹3丂偱丄俹丄俻偼摍妏嫟栶揰側偺偱丄佢俹俛俹3亖佢俻俛俻1丂傛傝丄
丂佢俹俹1俹3亖佢俻俛俻1丂偡側傢偪丄佢俽俹1俿亖佢俽俛俹1
丂佢俹1俽俛偼嫟捠側偺偱丄俀妏憡摍偐傜丄丂仮俽俛俹1佷仮俽俹1俿
丂偲偙傠偱丄佢俽俹1俛亖俋侽亱側偺偱丄佢俽俿俹1亖俋侽亱丂懄偪丄俛俻佦俹1俹3丂偑惉傝棫偮丅
掕棟丂丂仮俙俛俠偵偍偄偰丄摍妏嫟栶揰傪俹丄俻偲偡傞丅俹傛傝丄俁曈偵悅慄偺懌俹1丄俹2丄俹3傪
丂丂丂丂壓偡丅摨條偵丄俻傛傝丄俁曈偵悅慄偺懌俻1丄俻2丄俻3傪壓偡丅俹偺俹1丄俹2丄俹3丄俻1丄
丂丂丂丂俻2丄俻3偵娭偡傞懳徧揰傪俹1乫丄俹2乫丄俹3乫丄俻1乫丄俻2乫丄俻3乫偲偡傞偲丄偙偺俇揰偼丄俻
丂丂丂丂傪拞怱偲偡傞墌廃忋偵偁傞丅
丂丂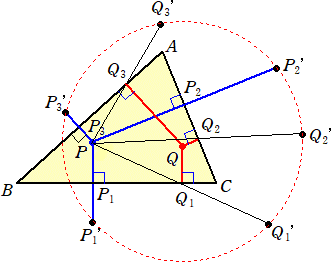
乮徹柧乯丂揰俹偵懳偟偰丄揰俹1乫丄俹2乫丄俹3乫丄俻1乫丄俻2乫丄俻3乫偺庢傝曽偐傜丄
丂仮俹1俹2俹3佷仮俹1乫俹2乫俹3乫丂丄仮俻1俻2俻3佷仮俻1乫俻2乫俻3乫丂乮憡帡斾丂俀乯丂偱偁傞丅
丂丂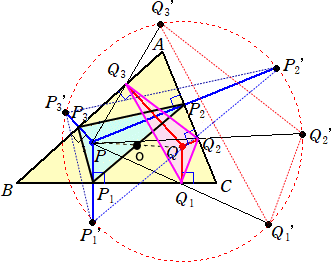
丂俇揰俹1丄俹2丄俹3丄俻1丄俻2丄俻3傪捠傞墌偼丄俇揰俹1乫丄俹2乫丄俹3乫丄俻1乫丄俻2乫丄俻3乫傪捠傞
墌偵憡帡奼戝偝傟傞丅
丂偦偺墌偺拞怱偼丄俹偵娭偟偰揰俷傪俀攞偵憡帡奼戝偡傟偽丄俻偲側傞丅丂丂乮徹廔乯
掕棟丂丂仮俙俛俠偵偍偄偰丄摍妏嫟栶揰傪俹丄俻偲偡傞丅俹傛傝丄俁曈偵悅慄偺懌俹1丄俹2丄俹3傪
丂丂丂丂壓偡丅摨條偵丄俻傛傝丄俁曈偵悅慄偺懌俻1丄俻2丄俻3傪壓偡丅俻偺俹1丄俹2丄俹3丄俻1丄
丂丂丂丂俻2丄俻3偵娭偡傞懳徧揰傪俹1乭丄俹2乭丄俹3乭丄俻1乭丄俻2乭丄俻3乭偲偡傞偲丄偙偺俇揰偼丄俹
丂丂丂丂傪拞怱偲偡傞墌廃忋偵偁傞丅
乮徹柧乯丂忋婰偲摨條偵偟偰帵偝傟傞丅丂丂乮徹廔乯
丂傝傜傂偄偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俆擭俇寧俁侽擔晅偗乯
丂堦斒壔偝傟偨乽揰偵娭偡傞嫟栶娭學乿(帺屓嫟栶側揰傪4偮帩偮傕偺)偵偮偄偰彂偒崬傫偱偍
偒傑偡丅
丂侾揰傪捠傞係捈慄偺暋斾傪 [l1,l2;l3,l4] 偺傛偆偵彂偒丄侾捈慄忋偵偁傞4揰偺暋斾傪
[P1,P2;P3,P4] 偺傛偆偵彂偔丅
丂揰D偼捈慄BC丄CA丄AB忋偵側偄偲偡傞丅係偮偺帺屓嫟栶側揰傪帩偪丄偦偺拞偺侾偮偑揰D
偱偁傞傛偆側嫟栶娭學偺偙偲傪D-嫟栶偲彂偔偙偲偵偟丄偁傞揰偵懳偟偰丄D-嫟栶偺娭學偵偁傞
揰偺偙偲傪D-嫟栶揰偲彂偔偙偲偵偡傞丅
亙D-嫟栶揰亜
丂捈慄BC丄CA丄AB忋偵側偄揰P偵懳偟偰丄捈慄m1偼揰A傪捠傝丄[AC,AB;AD,m1]亖侾/[AC,AB;AD,AP]
偲側傞捈慄偲偟丄捈慄m2偼揰A傪捠傝丄[BA,BC;BD,m2]亖侾/[BA,BC;BD,BP] 偲側傞捈慄偲偟丄
捈慄m3偼揰A傪捠傝丄[CB,CA;CD,m3]亖侾/[CB,CA;CD,CP] 偲側傞捈慄偲偡傞丅
丂偙偺偲偒丄俁杮偺捈慄m1丄m2丄m3偼侾揰偱岎傢傞丅偙偺揰偑揰P偺D-嫟栶揰偱偁傞丅
丂偪側傒偵丄捈慄BC偲AD偺岎揰傪A乫丄CA偲BD偺岎揰傪B乫丄AB偲CD偺岎揰傪C乫偲偡傞偲丄
D-嫟栶偺係偮偺帺屓嫟栶側揰偺偆偪揰D埲奜偺俁偮偺揰偼丄揰A丄A乫偵娭偡傞揰D偺挷榓嫟
栶揰丂丄揰B丄B乫偵娭偡傞揰D偺挷榓嫟栶揰丂丄揰C丄C乫偵娭偡傞揰D偺挷榓嫟栶揰偱偁傞丅
仸挷榓嫟栶揰偲偼暋斾偑-1偲側傞揰偺偙偲傪偄偆丅
丂堦斒壔偝傟偨乽捈慄偵娭偡傞嫟栶娭學乿(帺屓嫟栶側捈慄傪4偮傕偮傕偺)偵偮偄偰彂偒崬傫
偱偍偒傑偡丅
丂捈慄d偼揰A丄B丄C傪捠傜側偄偲偡傞丅傑偨丄捈慄d偲捈慄BC丄CA丄AB偺岎揰傪偦傟偧傟D1丄
D2丄D3偲偡傞丅
丂係偮偺帺屓嫟栶側捈慄傪帩偪丄偦偺拞偺1偮偑捈慄d偱偁傞傛偆側嫟栶娭學偺偙偲傪d-嫟栶
偲彂偔偙偲偵偟丄偁傞捈慄偵懳偟偰d-嫟栶偺娭學偵偁傞捈慄偺偙偲傪d-嫟栶慄偲彂偔偙偲偵偡傞丅
亙d-嫟栶慄亜
丂揰A丄B丄C傪捠傜側偄捈慄l偲捈慄BC丄CA丄AB偺岎揰傪偦傟偧傟L1丄L2丄L3偲偡傞丅
丂揰M1偼捈慄BC忋偵偁傝丄[B,C;D1,M1]亖侾/[B,C;D1,L1] 偲側傞揰偲偟丄揰M2偼捈慄CA忋偵
偁傝丄[C,A;D2,M2]亖侾/[C,A;D2,L2] 偲側傞揰偲偟丄揰M3偼捈慄AB忋偵偁傝丄
[A,B;D3,M3]=1/[A,B;D3,L3] 偲側傞揰偲偡傞丅
丂偙偺偲偒丄3偮偺揰M1丄M2丄M3偼1捈慄忋偵偁傞丅偙偺捈慄偑捈慄l偺d-嫟栶慄偱偁傞丅
丂偪側傒偵丄d-嫟栶偺4偮偺帺屓嫟栶側捈慄偺偆偪捈慄d埲奜偺3杮偺捈慄偼丄捈慄BC丄AD1
偵娭偡傞捈慄d偺挷榓嫟栶慄丄捈慄CA丄BD2偵娭偡傞捈慄d偺挷榓嫟栶慄丄捈慄AB丄CD3偵
娭偡傞捈慄d偺挷榓嫟栶慄偱偁傞丅
仸挷榓嫟栶慄偲偼暋斾偑-1偲側傞捈慄偺偙偲傪偄偆丅
丂丂埲壓丄岺帠拞両
丂丂丂丂丂丂丂丂丂丂丂丂丂丂














