(1) 各項は、1以上4以下の整数
(2) s≠t で、as=at ならば、as+1≠at+1
この性質を持つ数列で、m が最大となるものを構成してください。
例えば、 a1=a2=1 とすると、性質(2)より、 a2≠a3 なので、 a3≠1
よって、a3 は、性質(1)より、 2、3、4 の何れかとなる。
そこで、 a3=2 としてみる。すると、a4 は、 1、2、3、4 の何れかとなる。
そこで、 a4=1 としてみる。このとき、 a1=a2=a4=1 なので、性質(2)より、
a2≠a3、a2≠a5、a3≠a5 を満たすように、a5 を定めればよい。
a5 は、1と2以外の数なので、a5=3 としてみる。
すると、a6 は、 1、2、3、4 の何れかとなる。
・・・・・・・・・・・・・・・・・・・・・・・・・・・
その後を適当に値を決めていくと、
1、1、2、1、3、1、4、1
とした場合は、第9項に入るべき数がなくなるので、この場合は、「記録 m=8」となる。
多分、数の選択が悪かったんでしょう...。
違うパターンで考えてみると、
1、2、3、4、1、3、2、4、2、1、2
で、第11項目に「2」が入るのは誤りで、修正すると
1、2、3、4、1、3、2、4、2、1、4、3、1、1
で、第15項目に入る数はないので、この場合は、「記録 m=14」となる。
一体、どこまでmの値は伸ばせるのだろうか?これが、冒頭の問題の趣旨です。
らすかるさんからのコメントです。(令和5年5月3日付け)
多分、m の最大は、17 ですよね。
適当に考えたので全く綺麗ではないですが、例えば、
2、1、3、1、4、2、3、2、4、3、3、4、4、1、1、2、2
(コメント) お~、すばらしい!私も何とか、m=17の場合を構成することが出来ました!
1、2、3、4、3、2、4、1、3、3、1、4、4、2、2、1、1
作り方は、次の4×4のマス目で、あるマス目から始めて全てのマス目を動くように数を選
択していけばよいようです。上の場合だと、次の順番で選択しました。
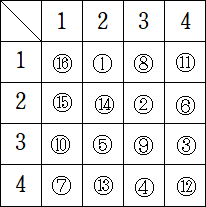
(am,an)の順序対で、上表の①は、(1,2)を意味し、数列を 1,2 と並べる。次に②は
(2,3)を意味し、数列を 1,2,3 と続けて並べる。③は、(3,4)を意味し、数列を
1,2,3,4 と続けて並べる。以下同様にして、m=17 の数列
1、2、3、4、3、2、4、1、3、3、1、4、4、2、2、1、1
が完成する。この構成法から、mの最大値が17であることも分かる。
Dengan kesaktian Indukmu さんからのコメントです。(令和5年5月4日付け)
m=17 で作ると、右端と左端とは同じものになりそうですね。
らすかるさんからのコメントです。(令和5年5月4日付け)
はい、両端は同じ数字になります。
ゾロ目が入っているとちょっとややこしいので、11、22、33、44 を除いた m=13 で考えます。
(m=17のパターンから同じ数字の連続を1文字減らせばそのパターンになります。)
また、先頭の数字は 2 とします。2 で始まる 2 桁は、21、23、24 の 3 個
2 で終わる 2 桁は、12、32、42 の 3 個が必要ですが、右端が 2 でないと仮定すると、
2a…A2b…B2c…
のようになり、2a、2b、2c の 3 個で、21、23、24 はすべて終わりますが、そうすると、2 で終
わるものが A2、B2 の 2 個しかないので足りません。
よって、2 で始まるものと 2 で終わるものが同数になるためには、
2a…A2b…B2c…C2
のように 2 で始まったら 2 で終わらなければなりませんので、左端と右端の数字は常に同
じになります。
Dengan kesaktian Indukmu さんからのコメントです。(令和5年5月4日付け)
らすかるさん、いつもありがとうございます。
DD++ さんからのコメントです。(令和5年5月4日付け)
1 までを使う場合、最長の 1 つは、 1、1
2 までを使う場合、これのどこかの 1 を 1、2、1 に変え、さらにどこかの 2 を 2、2 に変え
ると、 1、2、2、1、1
3 までを使う場合、これのどこかの 1 を 1、3、1 に変え、さらにどこかの 2 を 2、3、2 に変
え、そしてどこかの 3 を 3、3 に変えると、 1、3、3、1、2、3、2、2、1、1
以下同様に繰り返せば、n まで使うときの n^2+1 項の数列の一例を錬成できますね。
Dengan kesaktian Indukmu さんからのコメントです。(令和5年5月4日付け)
m=17 で所望の有限数列を求めるにあたり、1列の繋がりではなく、m-1=16 の数からなる
円環をまずは構成するのも面白いですね。
DD+さんによる構成を真似すれば、n が 4 のときも n^2 がベストなわけです。m-1=16はそ
れを満たしています。
四色のビーズに糸を通して輪っかにし、机の上においたときに、輪を右回りに方向づけて、
各ビーズの右隣、左隣の色のパターンがそれぞれ輪のなかでダブルことがないようにするに
は(四色でしたから)、4✕4 = 16 が最大であろうと見当がつきます。
うまく並べることができたら、輪っかの糸を一箇所で切断し、ビーズを1列に並ぶようにしま
す。このとき、切断のおかげで、色の並びのひとつが消失します。
それを補償するために、ビーズを1個補充して、左右の端の色が同じになるようにします。
これにて、17個で、左右の端が同じになる列ができあがります。
(論理が飛んでいますがご容赦ください。)
GAI さんからのコメントです。(令和5年5月4日付け)
使える数字が{1,2}や{1,2,3}ならどうなるのだろうと思ったので調べたら、
{1,2}=>[1,2,2,1,1],[1,1,2,2,1] (なお1,2の数字を入れ替えても可)で<1を3回;2を2回使用>
{1,2,3}=>[1, 1, 2, 1, 3, 2, 2, 3, 3, 1] (1,2,3の数字はサイクリックに変更できる。)で
<1を4回;2を3回;3を3回使用>
らすかるさんの例も、(1->4.2->1,3->2,4->3)に読み替えると、
{1,2,3,4}=>[1,4,2,4,3,1,2,1,3,2,2,3,3,4,4,1,1]で<1を5回;2を4回;3を4回;4を4回使用>
そこで、一般に、{1,2,3,・・・,n}の数字で条件を満たす最長のパターンは、
<1をn+1回;2をn回;3をn回;4をn回;・・・,nをn回使用>して最長n^2+1の数列
が作れそうです。証明は数学的帰納法が有力だが、示し方が分からない。
これが何通り構成可能かは、1を他より1回多く使用するパターンに限って調べたら、
n=2;2通り(例で挙げたもの)
n=3;72通り
1;[1, 1, 2, 1, 3, 2, 2, 3, 3, 1]
2;[1, 1, 2, 1, 3, 3, 2, 2, 3, 1]
3;[1, 1, 2, 2, 1, 3, 2, 3, 3, 1]
4;[1, 1, 2, 2, 1, 3, 3, 2, 3, 1]
5;[1, 1, 2, 2, 3, 1, 3, 3, 2, 1]
6;[1, 1, 2, 2, 3, 2, 1, 3, 3, 1]
7;[1, 1, 2, 2, 3, 3, 1, 3, 2, 1]
8;[1, 1, 2, 2, 3, 3, 2, 1, 3, 1]
9;[1, 1, 2, 3, 1, 3, 3, 2, 2, 1]
10;[1, 1, 2, 3, 2, 2, 1, 3, 3, 1]
11;[1, 1, 2, 3, 3, 1, 3, 2, 2, 1]
12;[1, 1, 2, 3, 3, 2, 2, 1, 3, 1]
13;[1, 1, 3, 1, 2, 2, 3, 3, 2, 1]
14;[1, 1, 3, 1, 2, 3, 3, 2, 2, 1]
15;[1, 1, 3, 2, 1, 2, 2, 3, 3, 1]
16;[1, 1, 3, 2, 2, 1, 2, 3, 3, 1]
17;[1, 1, 3, 2, 2, 3, 3, 1, 2, 1]
18;[1, 1, 3, 2, 3, 3, 1, 2, 2, 1]
19;[1, 1, 3, 3, 1, 2, 2, 3, 2, 1]
20;[1, 1, 3, 3, 1, 2, 3, 2, 2, 1]
21;[1, 1, 3, 3, 2, 1, 2, 2, 3, 1]
22;[1, 1, 3, 3, 2, 2, 1, 2, 3, 1]
23;[1, 1, 3, 3, 2, 2, 3, 1, 2, 1]
24;[1, 1, 3, 3, 2, 3, 1, 2, 2, 1]
25;[1, 2, 1, 1, 3, 2, 2, 3, 3, 1]
26;[1, 2, 1, 1, 3, 3, 2, 2, 3, 1]
27;[1, 2, 1, 3, 2, 2, 3, 3, 1, 1]
28;[1, 2, 1, 3, 3, 2, 2, 3, 1, 1]
29;[1, 2, 2, 1, 1, 3, 2, 3, 3, 1]
30;[1, 2, 2, 1, 1, 3, 3, 2, 3, 1]
31;[1, 2, 2, 1, 3, 2, 3, 3, 1, 1]
32;[1, 2, 2, 1, 3, 3, 2, 3, 1, 1]
33;[1, 2, 2, 3, 1, 1, 3, 3, 2, 1]
34;[1, 2, 2, 3, 1, 3, 3, 2, 1, 1]
35;[1, 2, 2, 3, 2, 1, 1, 3, 3, 1]
36;[1, 2, 2, 3, 2, 1, 3, 3, 1, 1]
37;[1, 2, 2, 3, 3, 1, 1, 3, 2, 1]
38;[1, 2, 2, 3, 3, 1, 3, 2, 1, 1]
39;[1, 2, 2, 3, 3, 2, 1, 1, 3, 1]
40;[1, 2, 2, 3, 3, 2, 1, 3, 1, 1]
41;[1, 2, 3, 1, 1, 3, 3, 2, 2, 1]
42;[1, 2, 3, 1, 3, 3, 2, 2, 1, 1]
43;[1, 2, 3, 2, 2, 1, 1, 3, 3, 1]
44;[1, 2, 3, 2, 2, 1, 3, 3, 1, 1]
45;[1, 2, 3, 3, 1, 1, 3, 2, 2, 1]
46;[1, 2, 3, 3, 1, 3, 2, 2, 1, 1]
47;[1, 2, 3, 3, 2, 2, 1, 1, 3, 1]
48;[1, 2, 3, 3, 2, 2, 1, 3, 1, 1]
49;[1, 3, 1, 1, 2, 2, 3, 3, 2, 1]
50;[1, 3, 1, 1, 2, 3, 3, 2, 2, 1]
51;[1, 3, 1, 2, 2, 3, 3, 2, 1, 1]
52;[1, 3, 1, 2, 3, 3, 2, 2, 1, 1]
53;[1, 3, 2, 1, 1, 2, 2, 3, 3, 1]
54;[1, 3, 2, 1, 2, 2, 3, 3, 1, 1]
55;[1, 3, 2, 2, 1, 1, 2, 3, 3, 1]
56;[1, 3, 2, 2, 1, 2, 3, 3, 1, 1]
57;[1, 3, 2, 2, 3, 3, 1, 1, 2, 1]
58;[1, 3, 2, 2, 3, 3, 1, 2, 1, 1]
59;[1, 3, 2, 3, 3, 1, 1, 2, 2, 1]
60;[1, 3, 2, 3, 3, 1, 2, 2, 1, 1]
61;[1, 3, 3, 1, 1, 2, 2, 3, 2, 1]
62;[1, 3, 3, 1, 1, 2, 3, 2, 2, 1]
63;[1, 3, 3, 1, 2, 2, 3, 2, 1, 1]
64;[1, 3, 3, 1, 2, 3, 2, 2, 1, 1]
65;[1, 3, 3, 2, 1, 1, 2, 2, 3, 1]
66;[1, 3, 3, 2, 1, 2, 2, 3, 1, 1]
67;[1, 3, 3, 2, 2, 1, 1, 2, 3, 1]
68;[1, 3, 3, 2, 2, 1, 2, 3, 1, 1]
69;[1, 3, 3, 2, 2, 3, 1, 1, 2, 1]
70;[1, 3, 3, 2, 2, 3, 1, 2, 1, 1]
71;[1, 3, 3, 2, 3, 1, 1, 2, 2, 1]
72;[1, 3, 3, 2, 3, 1, 2, 2, 1, 1]
n=4; 82944通り
1;[1, 1, 2, 1, 3, 1, 4, 2, 2, 3, 2, 4, 3, 3, 4, 4, 1]
2;[1, 1, 2, 1, 3, 1, 4, 2, 2, 3, 2, 4, 4, 3, 3, 4, 1]
3;[1, 1, 2, 1, 3, 1, 4, 2, 2, 3, 3, 2, 4, 3, 4, 4, 1]
・・・・・・・・・・・・・・・・
82942;[1, 4, 4, 3, 4, 2, 4, 1, 3, 3, 2, 2, 3, 1, 2, 1, 1]
82943;[1, 4, 4, 3, 4, 2, 4, 1, 3, 3, 2, 3, 1, 1, 2, 2, 1]
82944;[1, 4, 4, 3, 4, 2, 4, 1, 3, 3, 2, 3, 1, 2, 2, 1, 1]
怪しいプログラムで探しているので、誰か確認願う。
らすかるさんからのコメントです。(令和5年5月4日付け)
2、72、82944 は正しいです。また、n=5 は、4976640000通りです。
(コメント) 「2,72,82944,4976640000」は未だオンライン整数列大辞典には登録されてい
ないようです。
GAI さんからのコメントです。(令和5年5月4日付け)
n=4 での結果を得るまでに優に3時間以上は要したので、n=5 では指数関数的に時間が
増加し、自分のプログラムではたぶん1年以上かかっても無理と思えるものになります。
それを n=5 は 4976640000通りとたちどころに算出できるらすかるさんの技に驚かされます。
出題された問題が、どんなことを意味しているのかを理解するまでにまず時間がかかり、ら
すかるさんの解答をみて、やっとその意味が分かり始め、始めは配列を手作業で作ろうと試
みるが結局混乱していき、何とか自動化で配列を決められないかと、これをプログラムで作
り出すまでにまた何度も試行錯誤を繰り返していきました。
始め全部で配列が何個できるかを探る疑問に間違った考え方で算出していたが、結果を
点検したらその考え違いに気付いて、コードを全面的に修正してやっと何とか結果が得られ
たんではないかという顛末を辿りました。
自分なりに修正を繰り返しながら、らすかるさんと同じ結果を得られたことにとてもうれしい
気持ちです。
DD++ さんからのコメントです。(令和5年5月4日付け)
もしかして、
n=6 は 23219011584000000
n=7 は 11800915893414789120000000
n=8 は 873120530892689265453642547200000000
だったりします?コンピュータでも流石にこの桁数は厳しいですかね?
らすかるさんからのコメントです。(令和5年5月5日付け)
n=5 は数分だったのですが、n=6 にかかる時間はざっと考えても1兆倍以上かかりそうなの
で、コンピュータでカウントする方式では試すまでもなく全く無理ですね。
DD++ さんからのコメントです。(令和5年5月5日付け)
n まで使える場合に最長数列が何通り構成できるか。
その答えは、全く別の「ある問題」の答えを足がかりにするとよい、というところまで昨晩到
達し、実際に n=8 までの解を(合っているかどうかまだ不明ですが)求めました。
が、しかし、その「ある問題」を一般の n で解こうとして一晩考えても方針が全く思い浮かび
ません。みなさんの協力を求めるべく、「まち針の木」として出題しています。あっちが解けれ
ばこっちも解けるので、挑戦よろしくお願いします。
そういえば、冒頭の
違うパターンで考えてみると、
1、2、3、4、1、3、2、4、2、1、2、2
で、第13項目に入る数はないので、
の例では、第 11 項の時点で「1, 2」が 2 回登場してルール違反になっていますね。らすかる
さんが既に証明している通り、「数列がこれ以上続けられない」という現象は必ずスタートに
使った数字で起こるはずです。
(コメント) 確かに、誤りでした!
違うパターンで考えてみると、
1、2、3、4、1、3、2、4、2、1、2
で、第11項目に「2」が入るのは誤りで、修正すると
1、2、3、4、1、3、2、4、2、1、4、3、1、1
で、第15項目に入る数はないので、この場合は、「記録 m=14」となる。
と修正しました。
GAI さんからのコメントです。(令和5年5月5日付け)
n=9
gp > prod(i=0,8,floor((80+i)/9)!)
%368 = 12123409823952368497816099928432676175872000000000
n=10
gp > prod(i=0,9,floor((99+i)/10)!)
%369 = 39594086612242519324387557078266845776303882240000000000000000000
一般に、n なら、 prod(i=0,n-1,floor((n^2-1+i)/n)!) となりませんか?
DD++ さんからのコメントです。(令和5年5月5日付け)
(n!)^n/n と同じ式ですかね?
n=8 までは私が直接求めたので、(私が計算ミスをしていない限り)この式に一致する結果
になっています。そして、n≧9 でも多分成り立つんだろうなと私も思います。
でも、「成り立つと予想した」だけでは解けたとは言えません。解けたと宣言するには成り立
つ証明まで必要です。
DD++ さんからのコメントです。(令和5年5月5日付け)
「最長数列の総数」と「まち針の木」の関係について掲載しておきます。
一般の n のままだとわかりにくいので、「最長数列の総数」の n=4 という具体的な話で進め、
既に出ている 82944 通りという数を導出してみます。
まず、
「数列の現在の末尾の数が 4 回目以内の登場ならば、次に書くことができる数がまだ残っ
ている」は数列の作り方から明らかです。
よって、対偶を考えれば、
「次に書くことのできる数がもうないならば、現在の末尾の数は 5 回目以降の登場をして
いる」
ことがわかります。
しかし、条件:「s≠t で、a[s]=a[t] ならば、a[s+1]≠a[t+1]」の対偶
「s≠t で、a[s+1]=a[t+1] ならば、a[s]≠a[t]」
より、同じ数が複数回登場する場合、直前の数字は全て異ならなくてはいけません。
つまり、5 回以上登場できる数は、先頭にある 1 に限られます。
つまり、次に書くことのできる数がもうなくなった数列は、必ず 1 が「先頭」「1 の次」「2 の
次」「3 の次」「4 の次」を順不同に 1 回ずつ計 5 回登場した直後で終わっています。
さて、最長数列の個数を考えましょう。
まず、n=4 の最長数列を実際にたくさん作って、「1 以外の各数について、4 回目の登場の
次に何を書いたか」で分類します。
例えば、GAI さんのリストの先頭のものは、4 回目の 2 の次は 4、4 回目の 3 の次は 4、4
回目の 4 の次は 1、となっているので、
1;[1, 1, 2, 1, 3, 1, 4, 2, 2, 3, 2, 4, 3, 3, 4, 4, 1] -> [2->4, 3->4, 4->1]
と分類します。
さて、では同じ [2->4, 3->4, 4->1] に分類される数列は何個作れるでしょうか。
実は、これは非常に簡単な問題です。
先に示した通り、そのような数列は最長でもそうでなくても、行き詰まるのは必ず 5 回目の
1 が登場したときです。
そして、それは「先頭」「1 の次」「2 の次」「3 の次」「4 の次」が全て揃ったときになるはず
です。
ところが、4->1 という関係がある以上、4 が 4 回登場した後でないと「4 の次」は起こりま
せん。
したがって、4->1 という依存関係があれば、どんなに雑に数列を作っても、行き詰まる前
に 4 が 4 回登場することは絶対に保証されるのです。
さらに、4 が 4 回登場するのは「1 の次」「2 の次」「3 の次」「4 の次」が全て揃ったときにな
るはずですが、2->4, 3->4 という関係があるので、同様に 2 と 3 もどんなに雑に作っても 4
回登場することが保証されるのです。
つまり、
「1 の登場 4 回目までは次の数に 1,2,3,4 を任意の順で使う」
「2 の登場 3 回目までは次の数に 1,2,3 を任意の順で使う」
「3 の登場 3 回目までは次の数に 1,2,3 を任意の順で使う」
「4 の登場 3 回目までは次の数に 2,3,4 を任意の順で使う」
を守る限り、何をやっても自動的に [2->4, 3->4, 4->1] に分類される最長数列ができあがる
のです。
よって、その総数は 4!*3!*3!*3! = 5184 通りです。
これは [2->4, 3->4, 4->1] に限った話ではないので、分類それぞれの中で必ず 5184 個
の最長数列が作れることになります。
では、そのような分類は何組できるかということを考えます。
[2->a, 3->b, 4->c] の a, b, c を適当に選べばよいかというとそうではありません。例えば
[2->4, 3->2, 4->2] の場合。
2 と 4 はお互いに 4 回目の登場があるとしたら相手の 4 回目より後でないといけないとい
うループが発生しています。
つまりどんなにうまくやっても 2 や 4 の 4 回目が登場しないまま 5 回目の 1 が来て数列
が終わってしまうことを意味します。
よって、[2->4, 3->2, 4->2] という分類は存在しません。
あるいは [2->1, 3->2, 4->4] の場合。
2 と 3 については 4 回の登場が保証されます。しかし、4 については 4 回目の登場があ
るとしたら 4 回目の 4 より後でないといけないという自己ループが発生していますので、4
は 4 回目の登場がありません。
よって、これも最長数列には絶対にならず、[2->1, 3->2, 4->4] という分類はできません。
つまり [2->a, 3->b, 4->c] という名目の分類が存在するか否かは、依存関係にこのような
ループが発生しないか否かを考えればよいことになります。
そして、それは、「まち針の木」で 1 という針山と 2, 3, 4 というまち針を用意して、
2 は a の頭(a=1 なら針山)に刺す
3 は b の頭(b=1 なら針山)に刺す
4 は c の頭(c=1 なら針山)に刺す
という木が存在するか否かを考えればいいことになります。
3 本のまち針で作る木は 16 通りだとわかっています。
よって、このような依存関係の作り方は 16 通り、ゆえに、最長数列の分類も 16 組である
ことがわかります。
したがって、n=4 の最長数列の総数は 5184*16 = 82944 となります。
一般の n の場合も同様に考えることができて、
「n-1 本のまち針の木の総数」 * n! * (n-1)! * (n-1)! * …… * (n-1)! ( (n-1)! は全部で n-1 個)
と求められることがわかります。
さて、では、「まち針の木」の総数を求める式(証明付き)は? というのが現状私がたどり
着いている最先端です。
Dengan kesaktian Indukmu さんからのコメントです。(令和5年5月5日付け)
どうも、「de Bruijn sequence」(デ・ブライン数列)と密接な関わりがあるような気がしてまい
りました。
冒頭の問題は1列ですが、この左端と右端とを繋げて輪にします。繋げるにあたり、両端は
同じでしたが、片方は除去します。つまり、一列に n^2+1 の要素があったものを n^2 の要素
のある輪にします。
「de Bruijn sequence」の記事中で、
"The number of distinct de Bruijn sequences B(k, n) is (k!)kn-1/kn "
とあります。この記事で、冒頭の問題を調べている私達の目的においては、「n=2」で固定で
考えてよいです。B(k, n)ではなく、B(k, 2)を知りたいのです。
また、この記事における k は、私達が解こうとしていた問題の n に相当します。
このことを意識して、B(k, 2) を求める式をみてください。
さて、こうして得られる数は、輪にしていたものに対応して数えています。輪を切断して元の
一列にするには、k 倍する必要があります。
といった………、浅い読み方をしております。皆様からの御批正をお願いいたします。
DD++ さんからのコメントです。(令和5年5月5日付け)
なるほど、密接な関わりどころか、ほぼそのものですね。
しかし、2 種類の n 連続で重複を避ける方向から発展してきた都合上、n 種類の 2 連続
での話はあんまりないみたいですね。
でも、とりあえず予想している式が正しいという保証ができたことは大きな一歩です。ありが
とうございます。
「この問題はちゃんと解ける問題である」というのは数学において最大のヒントですからね。
らすかるさんからのコメントです。(令和5年5月6日付け)
その後プログラムを何度か高速化して、n=5 の時の 4976640000 通りが一瞬で求められ
るようになり、このプログラムで、n=6 について求めたところ、約23分で「23219011584000000
通り」と求まりました。
(同一数字の連続をなくしたものを数えてn(n-1)^(n-1)を掛けるようにしたのが主な高速化)
それでも n=7 は数え方を根本から変えないと無理そうです。
GAI さんからのコメントです。(令和5年5月6日付け)
prod(i=0,n-1,floor((n^2-1+i)/n)!) と (n!)^n/n の結果が同じものになるのが面白く、構造
を分析すると、
n=3 3!*2!*2!*(3^1)=3!*3!*2!=3!*3!*(3!/3)=(3!)^3/3
n=4 4!*3!*3!*3!*(4^2)=4!*4!*4!*3!=4!*4!*4!*(4!/4)=(4!)^4/4
n=5 5!*4!*4!*4!*4!*(5^3)=5!*5!*5!*5!*4!=5!*5!*5!*5!*(5!/5)=(5!)^5/5
n=6 6!*5!*5!*5!*5!*5!*(6^4)=6!*6!*6!*6!*6!*5!=6!*6!*6!*6!*6!*(6!/6)=(6!)^6/6
n=7 7!*6!*6!*6!*6!*6!*6!*(7^5)=7!*7!*7!*7!*7!*7!*6!=7!*7!*7!*7!*7!*7*(7!/7)=(7!)^7/7
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
#2つ目の所が prod(i=0,n-1,floor((n^2-1+i)/n)!) で、最後の部分が (n!)^n/n に対応して
いく。
ここに、DD++ さんのコメントと重ね合わせると、
「n-1 本のまち針の木の総数」 * n! * (n-1)! * (n-1)! * …… * (n-1)! ((n-1)!は全部で n-1個)
と求められることがわかります。
n=3 である場合のDD++ さんの解説にある、
つまり [2->a, 3->b, 4->c] という名目の分類が存在するか否かは、依存関係にこのような
ループが発生しないか否かを考えればよいことになります。
そして、それは、「まち針の木」で 1 という針山と 2, 3, 4 というまち針を用意して、
2 は a の頭(a=1 なら針山)に刺す
3 は b の頭(b=1 なら針山)に刺す
4 は c の頭(c=1 なら針山)に刺す
という木が存在するか否かを考えればいいことになります。
3 本のまち針で作る木は 16 通りだとわかっています。
(私はいまいち理解が及んでいませんが、この数が4^2の部分に相当しているのか?)
n=5 まではコンピュータで、 [1,1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4,5,5,5,5,5] を勝手に並び
変えたとき、例の数列の条件が満たされる配列総数が 4976640000 まで確認されている
のですから、n=5 での
5!*4!*4!*4!*4!*(5^3)=5!*5!*5!*5!*4!=5!*5!*5!*5!*(5!/5)=(5!)^5/5(=4976640000)
における 5^3=125 は、「まち針の木の総数」と解釈できるんですよね。
この形式をたどれば、一般に、nでの「まち針の木の総数」= n^(n-2) となりそうなんです
が、n>=8 でもそれでいいという証明が必要ということでしょうか?(→ 参考:「A000272」)
DD++ さんからのコメントです。(令和5年5月6日付け)
らすかるさん、ありがとうございます。n=6 も私の計算であっていたみたいですね。
GAI さん、n>=8 でもそれでいいという証明が必要ということでしょうか?
「それでいい」がどこからどこまでを指して「それ」と言っているのか判断がつきかねますが、
一般の n に対して、まち針の木の総数を求めたがっているというのはその通りです。
最初の数項を実際に求めてみれば続きの予測は立ちますが、実際に証明しようと思うと難
しく、難航しています。
DD++ さんからのコメントです。(令和5年5月7日付け)
今にして思えば、「/n」がついているのは最初の数を「1」に限定しているせいですね。最初
の数も任意にしてよいのであれば、最長数列の総数は (n!)^n 通りというとても整った結果に
なります。また、計算方法も先頭の数は任意である方がやりやすそうです。
ということで、「まち針の木」の方で wikipedia から拾ってきた発想をこの問題用に書き直し
つつ、「n まで使える場合の最長数列の総数は (n!)^n 通りである」の証明を以下に記述しま
す。以前の内容と重複する部分も含みます。わかりにくければ、トランプを使って実際に手
を動かすと助けになると思います。
条件を満たすような数列を以下のような方法で作ることを考えます。
1 から n までのカードの組を n セット用意します。それぞれを適当な順に積み重ねて、各
山に 1 番から n 番までの番号をつけておきます。
最初に初項 a[1] として 1 以上 n 以下の数を選びます。
a[1] 番の山の一番上のカードを手に取り、書いてあった数字を a[2] とし、カードは破棄し
ます。
a[2] 番の山の一番上のカードを手に取り、書いてあった数字を a[3] とし、カードは破棄し
ます。
以下、同様に繰り返します。
a[m] 番の山の一番上を手に取ろうとしたら既にその山にカードがなかった場合、a[m] を
末項として数列を終了します。
[例1] n=3, a[1]=1 で各山が上から順に
1 番の山:1, 3, 2
2 番の山:2, 1, 3
3 番の山:2, 3, 1
の場合、数列は 1, 1, 3, 2, 2, 1, 2, 3, 3, 1 となります。
[例2] n=3, a[1]=1 で、各山が上から順に
1 番の山:1, 3, 2
2 番の山:2, 1, 3
3 番の山:1, 2, 3
の場合、数列は 1, 1, 3, 1, 2, 2, 1 となります。
[例3] n=3, a[1]=1 で、各山が上から順に
1 番の山:1, 3, 2
2 番の山:2, 1, 3
3 番の山:1, 3, 2
の場合、数列は 1, 1, 3, 1, 2, 2, 1 となります。
n^2+1 項続く最長数列ができる場合というのは、n^2 枚ある全てのカードを破棄できる場合
ということになります。
そして、
「最長数列の内容」 と 「全て破棄できるようにカードを積み重ねて a[1] を選ぶ方法」
が一対一に対応することは数列の作り方からすぐにわかるので、結局カードを全部破棄で
きるような場合の数を考えればいいことになります。
では、カードを全て破棄することに関していくつか考察を行います。
まず、この操作は a[1] と異なる数のカードで終わることは絶対にありません。しかも、終
わったときには必ず a[1] と同じ数のカードが全ての山から破棄されています。
なぜなら、どこかの山でカードが足りなくなるのは「全ての山から a[1] と同じ数のカードを
引く」を達成し、最初の 1 回とあわせて a[1] 番の山からカードを引くのが n+1 回目になると
き以外ありえないからです。
そして、a[1] と異なる数のカードも全て破棄されるかどうかは、a[1] 番以外の山の一番下
のカードだけ見ればわかります。
例えば [例1] の場合、まず、a[1]=1 なので 1 のカードは全て破棄されることがわかります。
次に、3 のカードは全て破棄されることもわかります。
なぜなら 3 番の山の一番下に 1 のカードがあり、「3 のカードが全て破棄されるまで 3 番の
山の 1 のカードが破棄できない」という状態になっているからです。
終わるまでに必ず 1 のカードが全て破棄されるのですから、その前に 3 のカードが全て破棄
されることも達成されなければなりません。
さらに、2 のカードも全て破棄されることがわかります。
なぜなら 2 番の山の一番下に 3 のカードがあり、「2 のカードが全て破棄されるまで 2 番の
山の 3 のカードが破棄できない」という状態になっているからです。
終わるまでに 3 のカードが全て破棄されることは先ほど確認したので、その前に 2 のカード
が全て破棄されることも達成されなければなりません。
よって、[例1] は、実際に数列を作ってみなくても、1 も 2 も 3 も全て破棄される、つまり最長
数列ができることがわかります。
一方で [例2] の場合、3 のカードが全て破棄されることはありません。
なぜなら 3 番の山の一番下に 3 のカードがあり、「3 のカードが全て破棄されるまで 3 番の
山の 3 のカードが破棄できない」という状態になっているからです。
一般に、a[1]≠x で x 番の山の一番下に x のカードがある場合、その山は絶対に残ってし
まいます。
よって、[例2] は、実際に数列を作ってみなくても、最長数列にはならないことがわかります。
また、[例3] の場合も、2 および 3 のカードが全て破棄されることはありません。
なぜなら 2 番の山の一番下に 3 のカードがあり、同時に 3 番の山の一番下に 2 のカードが
あるため、
「2 のカードが全て破棄されるまで 2 番の山の 3 のカードが破棄できない」
「3 のカードが全て破棄されるまで 3 番の山の 2 のカードが破棄できない」
という状態になっているからです。
一般に、このような依存関係のループが発生すると、それらの山は絶対に残ってしまいます。
([例2] も単独でループしているとみなすことができます)
よって、[例3] は、実際に数列を作ってみなくても、最長数列にはならないことがわかります。
ループが存在しなければ、全ての数のカードについて直接的または間接的に a[1] と同じ数
のカードを全て破棄する前にそちらを全て破棄する必要があり、最長数列ができることが確
定します。
よって、最長数列になるどうかは、積み重ねるときに a[1] 番以外の山の一番下に来るカー
ドでループが発生しないかどうかだけを考えればいいことになります。
さて、では、カードを無作為に積み重ねて初項も無作為に選んだ場合に、最長数列を作れ
る確率がどのくらいになるか考えます。
まず、無作為にカードを積み重ねつつ初項を無作為に選ぶ方法として以下の手順を採用
します。
1 から n までのカード 1 組をシャッフルします。その後、1 番から n 番までの番号を 1 つ
無作為に選び、この山の番号とします。
改めて別の 1 から n までのカード 1 組をシャッフルします。その後、1 番から n 番までの
番号のうち重複しないものを 1 つ無作為に選び、この山の番号とします。
これを n 回繰り返すと、1 番から n 番までの山が完成します。そして、最後に作った山の
番号を a[1] として採用します。
この作り方であれば、n 個の山の積み重ね方 (n!)^n 通りと a[1] の選び方 n 通りの組、
全 n*(n!)^n 通りの起こりやすさが同様に確からしいといえます。
ここで、確率 P[k] (0≦k≦n) を「この山の作り方で k 個の山を作った段階で、最後に残る
ことが確定した山がまだどこにもない確率」と定義します。もちろん、P[0]=1 です。
このとき 1 - P[k+1]/P[k] は「k 個の山を作った段階で最後に残ることが確定した山がまだ
どこにもないという条件のもとで、k+1 個目の山を作ったせいで最後に残ることが確定した山
ができてしまう条件付き確率」です。
これは、0≦k≦n-2 の場合、k+1 個目の山をシャッフルしたときに一番下にきたカードが
x だったとして、
・x 番の山が k 番目までにまだなく、その x 番をk+1 番目の山につけてしまった
・x 番の山が k 番目までにもうあり、「x 番の山の一番下のカードは y」「y 番の山の一番下
のカードは z」……と辿って行き着いた未使用番号を k+1 番目の山につけてしまったの
どちらかが起こる確率であり、つまりは一番下のカードが何であるかに関係なく残ってい
る n-k 個の番号から特定の 1 個を引いてしまう確率になります。
よって、 1 - P[k+1]/P[k] = 1/(n-k) なので、 P[k+1]/P[k] = 1 - 1/(n-k) = (n-k-1)/(n-k)
であり、
P[n-1] = (1/2)*P[n-2] = (1/2)*(2/3)*P[n-3] = …… = (1/2)*(2/3)*……*((n-1)/n)*P[0] = 1/n
となります。
最後に作る山は、どんな順序になっても、a[1] の選び方を考えれば確率に影響は与えま
せん。
よって、 P[n] = P[n-1] = 1/n です。
これで、「n 個の山を無作為に作り、初項 a[1] を無作為に選んだ場合に、最長数列を作れ
る確率は 1/n である」ことがわかりました。
ところで、この山の作り方は n*(n!)^n 通りが同様に確からしく作れる方法でした。つまり、
最長数列を作れるようにカードの積み重ねて a[1] を選ぶ方法がそのうち N[n] 通りであると
すると、古典的確率の定義より、
N[n] / {n*(n!)^n} = 1/n
となります。したがって、分母を払って、
N[n] = (n!)^n
が得られました。
以下、工事中!
