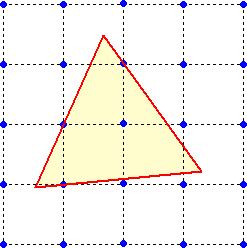
問題 xy平面上の正三角形で、内部(辺上を含まない)にちょうど一つ格子点(座標が整数
の点)を含むものの最大面積は?
GAI さんからのコメントです。(令和4年11月24日付け)
考えられる色々なパターンで、 (12+13*√3)/15=2.3011106998930・・・ が最大かなと思
いますが、絶対ですか?と言われれば、自信はありません。
らすかるさんからのコメントです。(令和4年11月24日付け)
残念ながら、それは最大ではありません。
例えば、一つの頂点を (0,2) として、残りの2頂点を x 軸上に置くだけで、その値より大き
くなりますね。
(参考) 面積=4/
GAI さんからのコメントです。(令和4年11月24日付け)
あら〜、基本的な形状から、この値を軽く超えてしまうとは・・・。
では、次の記録として、 3*√3/2(=2.5980762113533・・・) が出来ましたが、最大値と言え
るのか?
らすかるさんからのコメントです。(令和4年11月24日付け)
それより大きいものがあります。その三角形はちょっとスライドさせれば大きくできますね。
GAI さんからのコメントです。(令和4年11月24日付け)
再挑戦: (15+14*√3)/12(=3.270725942163690・・・)
手計算なので計算ミスが起こっているかも・・・。
らすかるさんからのコメントです。(令和4年11月24日付け)
大丈夫です。計算にミスはありません。私は最初、その値が最大だと思っていました。
しかしさらに計算していくと、それは最大ではないことがわかりました。そこから先の計算が
大変でした。
# 何かうまい方法があればひょっとすると簡単になるのかも知れませんが、少なくとも単純
に考えて計算していくと結構面倒です。
GAI さんからのコメントです。(令和4年11月24日付け)
これ以上の三角形が存在できるのか!信じられないですね〜。大きさでは小数点以下の
変化位なものですか? それとも整数部のオーダーも変化してしまう位なのですか?
らすかるさんからのコメントです。(令和4年11月24日付け)
小数点以下です。最大は、3.3 ちょい。
GAI さんからのコメントです。(令和4年11月25日付け)
3.30020486367181・・・・・・ 位ですか?
らすかるさんからのコメントです。(令和4年11月25日付け)
もう少し大きいです。3.309…
GAI さんからのコメントです。(令和4年11月25日付け)
コンピュータの数値計算の繰り返しで最大値になるものを絞り出す方法なので、時間をか
ける割にはこの程度の精度ですが、3.30940107・・・ 辺りでしょうか?
りらひいさんからのコメントです。(令和4年11月25日付け)
証明はしていませんが、3.3ちょいの値は出ました。結果だけ見るとシンプルに書けますね。
この答えが正しければ、普通の電卓でキーを7回叩けば数値が出ます。最大の証明はどう
すればいいんだろう。
らすかるさんからのコメントです。(令和4年11月25日付け)
GAI さん、「3.30940107・・・ 辺り」で正解です。
厳密値は、(4√3+3)/3=3.3094010767585…です。
下図で、正三角形の内部の点を原点とする。
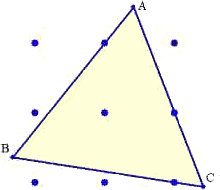
直線AB: y=(2+√3)x/3+1 、直線BC: y=(3-2√3)(x-1)/3-1 、直線CA: y=-(6+√3)(x-1)/3
で、 点A: ((9+√3)/26,11(9+√3)/78) 、点B: ((9-25√3)/26,(21-41√3)/78)
点C: ((35+√3)/26,-(19+5√3)/26)
一辺の長さ: (2/3)√(12+3√3)=2.764549…
面積: (4√3+3)/3=3.309401…
のようになります。
普通の図形問題のパターンだと、三角形がもっと安定する向きで最大になりそうな気がし
ますが、この問題ではなんとも中途半端な向きで最大になりますので、珍しいですね。
この角度で最大になることの証明は、以下のようにできます。
まず、原点だけを含むように正三角形を回転することを考えます。対称性から、回す角度
は 15°だけで十分であることがわかります。
図で、直線ABが y=x+1 である向きから直線BCが y=-1 である向きまでの 15°を考えます。
(AB上に、(0,1)、BC上に、(1,-1)、CA上に、(1,0) があるように回します)
確か、直線ABが y=x+1 のときの値が GAI さんが書かれた値 (15+14√3)/12=3.27…です
よね。
そして、直線BCが y=-1 である向きのときは、(3+2√3)/2=3.23… で、上の中途半端な角
度で 3.30… ですから、少なくともこの15°の途中に最大値があることがわかりますね。
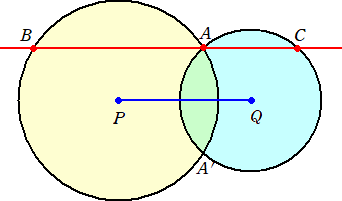
次に、上記の角度で最大値をとることの証明の肝の部分ですが、
まず、(1,0)・A・(0,1) のなす角が 60°であることから、Aは必ず点((3+√3)/6,(3+√3/6))を
通り、半径が √6/3 である円上にあることがわかります(この円は(1,0)と(0,1)を通ります)。
同様に、Cは必ず点 ((6+√3)/6,-1/2) を通り、半径が √3/3 である円上にあることがわか
ります(この円は(1,0)と(1,-1)を通ります)。
(いずれの円も、図の9点の格子点を使って容易に作図できます。作図方法は※1※2)
そして、(1,0)を通る直線と2円との(1,0)でない方の交点を結んだ線分の長さが最大になる
向きが答えになるわけですが、実は、これは2円の中心を結んだ直線と平行になるときが
最大であることがわかります(※3)。
それにより、上記の (4√3+3)/3 が最大となります。
※1 点Aの軌跡となる円の作図
「(-1,0)を中心として、(0,1)を通る円と、(0,1)を中心として、(-1,0)を通る円の交点のうち、yが
大きい方(-(1+√3)/2,(1+√3)/2)と(0,1)を結んだ直線」
と
「(0,-1)を中心として、(1,0)を通る円と、(1,0)を中心として、(0,-1)を通る円の交点のうち、yが
小さい方((1+√3)/2,-(1+√3)/2)と(1,0)を結んだ直線」
との交点を中心とし、(1,0)を通る円を描けばよい。
※2 点Cの軌跡となる円の作図
「(0,0)を中心として、(1,0)を通る円と、(1,0)を中心として、(0,0)を通る円の交点のうち、yが大
きい方(1/2,√3/2)と(1,0)を結んだ直線」
と
「(0,-1)を中心として、(1,-1)を通る円と、(1,-1)を中心として、(0,-1)を通る円の交点のうち、y
が小さい方(1/2,-1-√3/2)と(1,-1)を結んだ直線」
との交点を中心とし、(1,0)を通る円を描けばよい。
※3 「円Pと円Qが2点A、A’で交わり、点Aを通る直線と円P、QとのA以外の交点をB、Cとす
るとき、線分BCが最長になるのは、BC//PQ のときである」
という命題は、三角関数を使って強引に証明することはできましたが、おそらく幾何学的な証
明ができれば、そんなに長くはならない気がします。
どなたか証明できればお願いします。(既知の定理の場合は名前だけでも結構です)
りらひいさんからのコメントです。(令和4年11月25日付け)
らすかるさんの「(AB上に(0,1)、BC上に(1,-1)、CA上に(1,0)があるように回します」について、
これらの点(あるいはその対称移動)を通らない正三角形が最大になることがないのは、どの
ように言えばよいのでしょう。
わたしが証明していないといったのは、この配置以外の正三角形を検討していないからで
す。
図を眺めていれば感覚的にはわかるのですが、言葉にするのが難しいなと思って。
らすかるさんからのコメントです。(令和4年11月25日付け)
では、きちんと整理します。
前提は、「原点のみを内部に含む正三角形」です。
・各辺上(端点を除く)に少なくとも1点ないと最大にならない
(格子点を通らない辺の方向に拡大できるから)
・各辺上にある格子点は原点のまわりの8点に限られる
(それより外側の点を通ると原点以外の格子点を内部に含んでしまう)
4点(±1,±1)について
・対角の2点を通ると原点以外の点を含んでしまうので不適
・隣接2点を通る場合の面積の最大値は(3+2√3)/2=3.23…なので最大ではない
(隣接2点が異なる辺上にあると原点以外を含んでしまうので同一辺上の必要がある)
・従って、面積が最大となるとき、角の4点は通っても最大1つ
・角の4点を一つも通らず、残りの4点中3点を(1辺に1点として)通る場合、一応そのような正
三角形は存在するが、面積が 3(17889+10694√3)/34810=3.138… 未満になるので最大
にはならない
(ABが(0,1)を通りBCが(0,-1)を通りCAが(1,0)を通るとして計算しました)
従って、面積が最大となるとき、角の4点のうちちょうど1点を通る
これを(1,-1)としてよい。またBCがこの点を通るとしてよい。
このとき考えられるパターンは、
(1)ABが(-1,0)を通りCAが(0,1)を通る
(2)ABが(-1,0)を通りCAが(1,0)を通る
(3)ABが(0,1)を通りCAが(1,0)を通りBがy=x+1より上
(4)ABが(0,1)を通りCAが(1,0)を通りBがy=x+1より下
の4通り
(1)の場合
直線BCがy=-1に一致し、ABが(-1,0)を通り、CAが(0,1)を通る形(このとき、面積は、
(3+2√3)/2=3.23…)から、(-1,0)と(0,1)と(1,-1)を通ることを変えずに三角形を右回転していく
(Cが(1,-1)に一致するまで)と、Bと(1,-1)の距離とCと(1,-1)の距離はどちらも短くなっていくの
で、面積は最大にならない。
(BCが短くなっていくのは、BとCの軌跡の円を描けば自明です)
(2)の場合
ABが(-1,0)と(0,1)を通り、CAが(1,0)を通り、BCが(1,-1)を通る形(このとき面積は、
(15+14√3)/12=3.27…)から、(-1,0)と(1,0)と(1,-1)を通ることを変えずに三角形を右回転して
いく(Cが(1,-1)に一致するまで)と、Aと(1,0)の距離及びCと(1,0)の距離はどちらも短くなって
いくので、面積は最大にならない。
(CAが短くなっていくのは、AとCの軌跡の円を描けば自明です)
(3)の場合
BCが(-1,0)と(1,-1)を通り、CAが(1,0)を通り、ABが(0,1)を通る形(このとき面積は上に書い
た 3(17889+10694√3)/34810=3.138…) から、(0,1)と(1,0)と(1,-1)を通ることを変えずに三角
形を右回転していく(Cが(1,-1)に一致するまで)と、上と同様にCAは短くなっていくので、面
積は最大にならない。
(4)の場合
前回に書いたとおりで、この場合に最大値をとります。
従って、(4√3+3)/3 が最大値です。
GAI さんからのコメントです。(令和4年11月26日付け)
手探りで最大面積を微妙に数値を変化させながら、とても探していくのに時間が掛かって
いたので、何とか一発で辿り着けないものかと挑戦してみました。
正三角形の内部に唯一含まれる格子点の周りの8個の格子点のどこを通らせる3つの直
線が有効であるかを決定するまでの前段階が長い道のりがかかるが、もし内部の格子点
を(1,0)と指定しておけば(らすかるさんは(0,0)とされていた。)、囲む3つの直線を格子点
P(0,0),Q(0,-1),R(1,1)で指定してやれば良く、それぞれの点を通る直線の傾きをm1,m2,m3で
表せば、
Pを通る直線はy=m1*x・・・・・・・・・・・・・(*)
Qを通る直線はy=m2*x-1・・・・・・・・・・・(**)
Rを通る直線はy=m3*x+1-m3・・・・・・・(***)
(*)(**)の交点をA、(**)(***)の交点をB、(***)(*)の交点をCで表すと、
A(1/(m2-m1),m1/(m2-m1))
B((2-m3)/(m2-m3),(m2+m3-m2*m3)/(m2-m3))
C((1-m3)/(m1-m3),m1*(1-m3)/(m1-m3))
となり、(1,0)を取り囲む三角形の各頂点に相当する。
ここに、△ABCが正三角形をなすことから、m1,m2には、
(m1-m2)/(1+m1*m2)=tan(Pi/3)=√3 よって、m2=(m1-√3)/(√3*m1+1)
同じく、m1,m3には、 (m3-m1)/(1+m3*m1)=√3 よって、m3=(√3+m1)/(1-√3*m1)
の関係式が成立する。
これを使えば、点A,Cの座標は、
A(-(√3*m1+1)/(√3*(m1^2+1)),-m1*(√3*m1+1)/(√3*(m1^2+1)))
C((√3-1+(√3+1)*m1)/(√3*(m1^2+1)),m1*(√3-1+(√3+1)*m1)/(√3*(m1^2+1)))
と、m1のパラメータのみで表せ、2点A,Cの距離Lは、
L^2=AC^2=((2*√3+1)*m1+√3)^2/(3*(m1^2+1))
そこで、m1の部分を変数xにして、
f(x)=((2*√3+1)*x+√3)^2/(3*(x^2+1))
なる分数関数の増減を調べる。
例により微分すると(計算が結構大変)、
f'(x)=-2*(6+√3)*(x^2-2/33*(24+7*√3)*x-1)/(3*(x^2+1)^2)
=-2*(6+√3)*(x-(6+√3)/3)*(x+(6-√3)/11)/(3*(x^2+1)^2)
f'(x)=0 から、x=(6+√3)/3,-(6-√3)/11
増減を調べて、x=(6+√3)/3 で、f(x)は極大で最大値を与える。
したがって、求める最大の三角形の面識Sは
S=1/2*L^2*sin(Pi/3)=1/2*f((6+√3)/3)*√3/2=(3+4*√3)/3(=3.309401076758503・・・・・・・)
と求められました。
ちなみに、A,B,Cの各交点を複素平面上で、Z1,Z2,Z3とすると、
Z1 = 1/(m2 - m1) + m1/(m2 - m1)*I
Z2 = ((-m3 + 2)/(m2 - m3)) + (((-m3 + 1)*m2 + m3)/(m2 - m3))*I
Z3 = ((-m3 + 1)/(m1 - m3)) + (-m3 + 1)*m1/(m1 - m3)*I
に置き換え、正三角形をなすであろう
m1=(6+sqrt(3))/3
%946 = 2.5773502691896257645091487805019574557
m2=(m1-sqrt(3))/(sqrt(3)*m1+1)
%947 = 0.15470053837925152901829756100391491130
m3=(sqrt(3)+m1)/(1-sqrt(3)*m1)
%948 = -1.2440169358562924311758154471686241223
の数値を
FR(m1,m2,m3)=real(Z1^2+Z2^2+Z3^2-Z1*Z2-Z2*Z3-Z3*Z1)
FR(m1,m2,m3)=imag(Z1^2+Z2^2+Z3^2-Z1*Z2-Z2*Z3-Z3*Z1)
へ代入すると、
gp > FR(m1,m2,m3)
%949 = 6.281303159995074080 E-38
gp > FI(m1,m2,m3)
%950 = -3.589316091425756617 E-38
つまり、公式(→ 参考:「複素数の底力」)
ガウス平面上の異なる3点 α、β、γ について、△αβγ が正三角形であるため
の必要十分条件は、
α^2+β^2+γ^2−αβ−βγ−γα=0
に合致しました。
実は、このことを利用して数値的に最大値の面積を探りにいっていました。
りらひいさんからのコメントです。(令和4年11月26日付け)
らすかるさん、詳しい説明をありがとうございます。まだ、ざっと読んだだけなので、後でしっ
かり読み込もうと思います。思った通り、というよりも思った以上に大変そうです。
<※3 の証明>です。
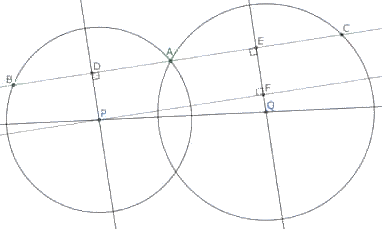
二つの円の中心P、Qから直線BCに下ろした垂線の足をそれぞれD、Eとすると、
BC=AB+AC=2*AD+2*AE=2*DE
点Pから直線QEに下ろした垂線の足をFとすると四角形PDEFは長方形なので、DE=PF
直角三角形PQFで三平方の定理より、PF=√(PQ^2-QF^2)
以上から、BCが最大となるのはQとFが一致するときで、このとき、BC//PQ
思いついてみれば単純でした。
らすかるさんからのコメントです。(令和4年11月26日付け)
おぉ!こんなに単純だったんですね。ありがとうございます。とてもすっきりしました。
最長のとき、BC=2PQ というのも知れてよかったです。
思った通り、というよりも思った以上に大変そうです。
そうですね。あれでも細部は説明が大変で省略してしまっていますので、すべての詳細を
書いたら、さらに数倍大きくなりそうです。もっとも、私の証明が下手で、もっと簡潔に示す方
法がある気もしますが...。
りらひいさんからのコメントです。(令和4年11月27日付け)
せっかくなので、私が「AB上に(0,1)、BC上に(1,-1)、CA上に(1,0)」と等価な配置における最
大面積を求めた時の計算過程を載せておきます。
といっても、座標で一辺の長さを出して微分で停留点を求めるという面白みのない方法で
すが...。それでも運よく(?)二重根号が外れたり約分ができたりして楽しかったので...。
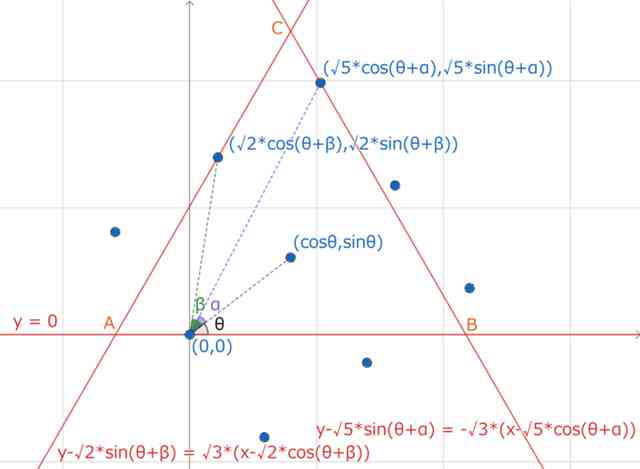
上図のように正三角形の一辺ABを x 軸上にとり、格子点を回転させる。
AB上の格子点を(0,0)とする。x 軸正の向きから測った正三角形内部の格子点方向の角度
をθとする。θの範囲は、30°≦θ≦45°になる。
辺BC上の格子点の座標は、(√5*cos(θ+α),√5*sin(θ+α))
辺CA上の格子点の座標は、(√2*cos(θ+β),√2*sin(θ+β))
となる。ここで、cosα=2/√5、sinα=1/√5、cosβ=1/√2、sinβ=1/√2 である。
辺BCの傾きは、-√3 なので、直線BCは、y-√5*sin(θ+α)=-√3*(x-√5*cos(θ+α)) 、
辺CAの傾きは、√3 なので、直線CAは、y-√2*sin(θ+β)=√3*(x-√2*cos(θ+β)) となる。
点B、Aは、それぞれの直線の x 切片なので、y=0 を代入すれば、
B(√5*cos(θ+α)+√5/√3*sin(θ+α),0) 、A(√2*cos(θ+β)-√2/√3*sin(θ+β),0)
となる。よって、正三角形の一辺の長さf(θ)は、
f(θ)=(点Bのx座標)-(点Aのx座標)
=√5*cos(θ+α)+√5/√3*sin(θ+α)-√2*cos(θ+β)+√2/√3*sin(θ+β)
=√5*(cosθ*cosα-sinθ*sinα)+√5/√3*(sinθ*cosα+cosθ*sinα)
-√2*(cosθ*cosβ-sinθ*sinβ)+√2/√3*(sinθ*cosβ+cosθ*sinβ)
=√5*(cosθ*2/√5-sinθ*1/√5)+√5/√3*(sinθ*2/√5+cosθ*1/√5)
-√2*(cosθ*1/√2-sinθ*1/√2)+√2/√3*(sinθ*1/√2+cosθ*1/√2)
=(2*cosθ-sinθ)+1/√3*(2*sinθ+cosθ)-(cosθ-sinθ)+1/√3*(sinθ+cosθ)
=(1+2/√3)*cosθ+√3*sinθ
微分して、f'(θ)=-(1+2/√3)*sinθ+√3*cosθ が0になるのは、
tanθ=√3/(1+2/√3)=3*(2-√3)
のときであり、これは 30°≦θ≦45°の範囲にある。
f'(30°)=1-1/√3>0 、f'(45°)=-1/√2*(1-1/√3)<0 なので、その間は上に凸で極大点
となる。
※ f''(arctan(3*(2-√3))=-f(arctan(3*(2-√3))<0 (∵ fは長さで正だから) なので極大と
した方がかっこよかったかも。
θm=arctan(3*(2-√3)) とすると、
cos(θm)^2=1/(1+tan(θm)^2)=(16+9*√3)/52
sin(θm)^2=1-cos(θm)^2=(36-9*√3)/52=9*(4-√3)/52
cos(θm)>0 、sin(θm)>0 より、
cos(θm)*sin(θm)=3/52*√((16+9*√3)*(4-√3))=3/52*√(37+20*√3)=3*(5+2*√3)/52
よって、このタイプの面積最大の正三角形の面積は、
√3/4*f(θm)^2
=√3/4*((1+2/√3)*cos(θm)+√3*sin(θm))^2
=√3/4*((1+2/√3)^2*cos(θm)^2+2*(1+2/√3)*√3*cos(θm)*sin(θm)+(√3)^2*sin(θm)^2)
=√3/4*((7+4*√3)/3*(16+9*√3)/52+(4+2*√3)*3*(5+2*√3)/52+3*9*(4-√3)/52)
=√3/(4*52*3)*((7+4*√3)*(16+9*√3)+9*(4+2*√3)*(5+2*√3)+81*(4-√3))
=√3/(4*52*3)*(832+208*√3)
=√3*/3*(4+√3)
=(3+4*√3)/3
である。
以下、工事中!
