放物線に関するちょっとした発見です。これは、ある日せっせと微積分〜(まちぼうけの
リズムで)していて見つけたものです。
放物線の準線と焦点が、
準線 : 放物線上の任意の点における接線 L と、それと直交するもう1本の接線 M
との交点の軌跡
焦点 : L と M のそれぞれの接点を通る直線(割線)と放物線の軸との交点
で求まるのです。(準線と焦点については、こちらを参照)
上記の性質は、平行移動、回転移動により不変な性質であり、また、全ての放物線は、
平行移動と回転移動により標準形に直せるので、標準形で確かめれば十分でしょう。
放物線の方程式(標準形)を、 y2=4px (p≠0) とすると、
準線は、 x=−p 、 焦点は、 ( p , 0 )
である。
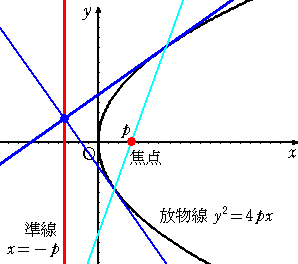
いま、放物線上の2点P( x1 , y1 ) 、Q( x2 , y2 )における接線の方程式は、
yy1=2p(x+x1) 、 yy2=2p(x+x2)
と書ける。 2つの放物線は垂直なので、 2p・2p+(−y1)(−y2)=0
すなわち、 y1・y2 = −4p2 が成り立つ。
このとき、 yy1y2=2py2(x+x1) 、 yy1y2=2py1(x+x2) より、
4p(y1−y2)x=4p(x1y2−x2y1)=y12y2−y1y22=−4p2(y1−y2)
y1≠y2 なので、 x=−p となる。
したがって、互いに垂直な2つの接線の交点の軌跡は、放物線の準線である。
ところで、 2つの接線の交点の座標を、( −p , q ) (qは、pの関数) とすると、
qy1=2p(−p+x1) 、 qy2=2p(−p+x2)
が成り立つので、 方程式 qY=2p(−p+X) は、2つの接点を通る直線を表す。
この直線と放物線の軸 Y=0 との交点は、 ( p , 0 ) となる。
したがって、 2つの接点を結ぶ直線と放物線の軸との交点は、放物線の焦点である。
(塾長コメント) この性質は非常に有名で、40年以上前から既に入試問題に登場してい
る。接線は、接点( x1 , y1 )と点( −x1 , 0 )を結ぶ直線として作図でき、
放物線の準線、焦点も方程式からすぐ分かるので、一つの接線に垂直な
接線を作図するときに有用な性質と言える。
上記の計算では、実際の交点を求めず、巧妙なアイデアを駆使している。
このアイデアに私が初めて接したのは高校2年のときである。そのときは、
「?」という感じで、イマイチ馴染めなかった。もしかしたら読者の方にも同
じ感慨の方がおられるかもしれない。このアイデアは習うより慣れろで、使
いこなしているうちに段々とその素晴らしさがヒシヒシと伝わってくることだ
ろう。
(補足) 平成17年6月19日、3類生さんから当HPの掲示板「出会いの泉」に書き込みを
頂いた。
前回、放物線の性質について投稿いたしましたが、その後、楕円と双曲線についても
調べてみました。結果は・・・円になります。(楕円については、現在自分が通ってい
る大学で過去に入試で出題されてましたが)ただ、実際に軌跡の方程式を求める際に、
「円だ」と予想しないと、トンデモナイことになる割に、結果がすっきりなのには、い
い意味でも悪い意味でも驚きましたね。
3類生さんに啓発されて私も計算してみた。すると、放物線、楕円、双曲線に関係なく、統
一的な解法が存在することに気づかされた。
放物線の場合 : 放物線の方程式を、 Y2=4pX (p≠0) とする。
互いに垂直な2つの接線の交点 P の座標を、( x , y ) とおく。
点 P を通り、傾き 1/m の直線の方程式は、 X = m( Y − y ) + x
これを、放物線の方程式に代入して、
Y2−4pm Y + 4pmy − 4px = 0
接する条件から、判別式を D とすると、
D/4 = 4p2m2 − 4pmy + 4px = 0
この2つの解を、m1、m2 とすると、解と係数の関係と垂直条件から、
m1・m2 = x/p = −1
よって、点 P が満たす軌跡の方程式は、 x = −p (準線) となる。
楕円の場合 : 楕円の方程式を、 b2X2 + a2X2=a2b2 ( a>b>0 ) とする。
互いに垂直な2つの接線の交点 P の座標を、( x , y ) とおく。
点 P を通り、傾き m の直線の方程式は、 Y = m( X − x ) + y
これを、楕円の方程式に代入して、整理すると
( b2 + a2m2 )X2 + 2ma2 ( y − mx )X + a2( y − mx )2 −a2b2 = 0
接する条件から、判別式を D とすると、
D/4 = a2b2(( a2 − x2 )m2 + 2mxy + b2 − y2 )= 0
a2 − x2 = 0 すなわち、 x = ±a のとき、条件を満たす点 P は、
( ±a , ±b ) (複号任意)
の4点ある。
a2 − x2 ≠ 0 のとき、
( a2 − x2 )m2 + 2mxy + b2 − y2= 0
は、m に関する2次方程式である。
この2つの解を、m1、m2 とすると、解と係数の関係と垂直条件から、
m1・m2 = ( b2 − y2 )/( a2 − x2 ) = −1
よって、点 P が満たす軌跡の方程式は、上記4点も含めて、
円 : x2 + y2 = a2 + b2
となる。
双曲線の場合 : 双曲線の方程式を、 b2X2 − a2X2=a2b2 ( a>b>0 ) とする。
互いに垂直な2つの接線の交点 P の座標を、( x , y ) とおく。
点 P を通り、傾き m の直線の方程式は、 Y = m( X − x ) + y
これを、双曲線の方程式に代入して、整理すると
( b2 − a2m2 )X2 − 2ma2 ( y − mx )X − a2( y − mx )2 −a2b2 = 0
接する条件から、判別式を D とすると、
D/4 = −a2b2(( a2 − x2 )m2 + 2mxy − b2 − y2 ) = 0
a2 − x2 = 0 すなわち、 x = ±a のとき、条件を満たす点 P はない。
よって、 a2 − x2 ≠ 0 としてよい。このとき、
( a2 − x2 )m2 + 2mxy − b2 − y2 = 0
は、m に関する2次方程式である。
この2つの解を、m1、m2 とすると、解と係数の関係と垂直条件から、
m1・m2 = ( −b2 − y2 )/( a2 − x2 ) = −1
よって、点 P が満たす軌跡の方程式は、 x2 + y2 = a2 − b2 となる。
(コメント) 直線も無限遠点を考えれば円の一部な訳で、これは円錐曲線の特有の性質な
のでしょうか?
