例えば、 三角形・二等辺三角形・正三角形・四角形・台形・長方形・正方形など。
しかし、どのような平面を準備しても決して現れることのない図形も存在する。
例えば、 直角三角形・直角二等辺三角形・一般の平行四辺形・一般のひし形など。
これらの図形が、どのような場合に出来て、どのような場合に出来ないのかをイメージす
ることは楽しい。
Dengan kesaktian Indukmu さんからのコメントです。（令和４年７月７日付け）
遠い昔の記憶を掘り起こしまして、次のような立体パズルがあったはずと朧気ながらに思
い出しました。
・正四面体を３つのピースで組み立てます。
・各ピースの体積は正四面体の体積の１/３です。
・３つのピースは互いに合同です。
・ピースは凹多面体です。
・ピースは面対称な立体です。（鏡像と合同）
※凸多面体ならば容易に想像できますが、凹多面体なのです。
実際に売られていた立体パズルでは、これらの３つのピースがひとつの小さな素朴なビニ
ール袋に封入されていて、全部を使って正四面体をつくれますかと煽るタイプだったような気
がします。買いませんでした、すみません。
Dengan kesaktian Indukmu さんからのコメントです。（令和４年７月１３日付け）
当該のパズルが復刻されていました。《売り切れとのこと》 （→ 「パズラボwebShop」）
（追記） 令和４年８月８日付け
正四面体を、一つのある辺を含み、それとねじれの位置にある辺の中点を通る平面で切
断するとき、その切り口は、２等辺三角形となる。
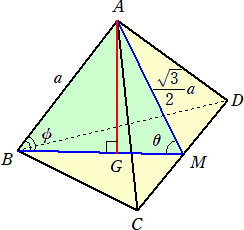
いくつか基本的な計量を計算してみよう。
ＢＭ＝（
/２）ａ で、Ｇは△ＢＣＤの重心である。ＢＧ ： ＧＭ＝２ ： １ なので、ＢＧ＝（
/２）ａ×（２/３）＝（/３）ａ 、ＧＭ＝（/６）ａよって、 ｃｏｓθ＝１/３ 、ｃｏｓφ＝１/
となる。このとき、 ｓｉｎθ＝２
/３ 、 ｓｉｎφ＝
/３ で、 ＡＧ＝（/３）ａまた、△ＡＢＭの面積は、 （
/２）ａ×（/３）ａ×（１/２）＝（/４）ａ2（コメント） 上図のθは、２面角で、いろいろな計算で頻出する角である。
次に、正四面体を平面で切断するとき、その切り口が正方形の場合について考えてみよう。
正四面体ＡＢＣＤにおいて、ねじれの位置にある２辺、例えば、ＡＣ、ＢＤを残して、残り４辺
の中点Ｐ、Ｑ、Ｒ、Ｓを通る平面を考えれば、ちょうど正四面体の切り口は正方形ＰＱＲＳとな
る。
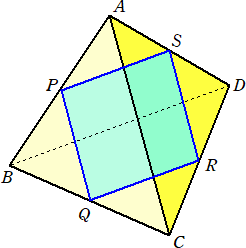
中点連結定理より、四角形ＰＱＲＳが４辺の長さが等しい平行四辺形、即ち、ひし形となる
ことは明らかだろう。
ひし形では、当然、次の性質が成り立つ。
１．線分ＰＲ⊥線分ＱＳ である。
対角線ＰＲ、ＱＳの交点をＯとすると、△ＰＱＯ≡△ＰＳＯ から、ＰＲ⊥ＱＳ が成り立つこと
は容易に分かるだろう。
ベクトルを用いて、次のように証明してもいいだろう。
（証明） ＡＢ＝２ｂ、ＡＣ＝２ｃ、ＡＤ＝２ｄ とおくと、
ＡＰ＝ｂ 、ＡＱ＝ｂ＋ｃ 、ＡＲ＝ｃ＋ｄ 、ＡＳ＝ｄ
よって、 ＰＲ＝ｃ＋ｄ−ｂ 、ＱＳ＝ｄ−ｂ−ｃ となるので、
ＰＲ・ＱＳ＝（ｃ＋ｄ−ｂ）・（ｄ−ｂ−ｃ）＝｜ｄ−ｂ｜2−｜ｃ｜2＝０
したがって、 ＰＲ⊥ＱＳ が成り立つ。 （終）
さらに、このひし形ＰＱＲＳは次のような性質を持つことが分かる。
２．∠ＱＰＳ＝９０° である。（→ この結果より、ひし形ＰＱＲＳは、正方形と言える。）
（証） ＰＱ＝ｃ 、ＰＳ＝ｄ−ｂ より、 ＰＱ・ＰＳ＝ｃ・（ｄ−ｂ）＝ｃ・ｄ−ｃ・ｂ＝０
したがって、 ∠ＱＰＳ＝９０° が成り立つ。 （終）
一つの正四面体に対して、このような正方形は、３つ出来る。
（追記） 令和４年８月５日付け
正四面体のある平面による切り口が正方形と聞くと、昔懐かしいチマキを思い出す。
丁度、正四面体のねじれの位置にある２辺を除いた４辺の中点を通るように紐で結んで
あったように思う。
同様にして、正八面体をある平面で切断するとき、その切り口が正六角形になる場合が
あり、そのような正六角形は全部で４通りある。下図と是非睨めっこして堪能してみてくだ
さい。
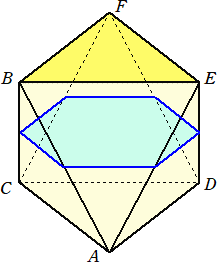
上記の正四面体内の正方形の存在から、正八面体を構成出来ることに気づく。
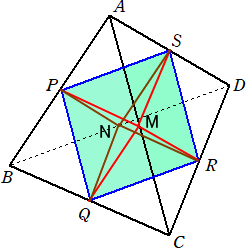
正方形の構成で用いなかった正四面体の２辺ＡＣ、ＢＤの中点をそれぞれＭ、Ｎとする。
正四面体から、小正四面体ＡＰＭＳ、ＣＱＲＭ、ＢＰＱＮ、ＤＳＲＮを切り取ると、正八面体が
得られる。
１辺の長さが ａ の正四面体の体積は、（
/１２）ａ3 なので、１辺の長さが ａ/２ の正八面体の体積は、
（
/１２）ａ3−（/１２）（ａ/２）3×４＝（/２４）ａ3となる。すなわち、１辺の長さが ａ の正八面体の体積は、
（
/２４）（２ａ）3＝（/３）ａ3となる。（→ 参考：「正多面体が５種類しかない理由」）
このことから、１辺の長さが等しい場合の正四面体と正八面体の体積比は、
（
/１２）ａ3 ： （/３）ａ3＝１ ： ４となる。この比は次のようにしても分かる。
正四面体から切り取る小正四面体の体積は、元の正四面体の１/８である。したがって、
中の正八面体の体積は、元の正四面体の １−（１/８）×４＝１/２ である。正四面体と正
八面体の１辺の長さが等しいとするならば、 （１/２）×２3＝４ となるので、正四面体と正
八面体の体積比は、 １ ： ４ であると言える。
（追記） 令和４年８月４日付け
上記で調べたように、一つの正四面体から、４つの小正四面体を切り取れば、正八面体が
構成できる。この知識があれば、逆に、正八面体の一つの面に正四面体が滑らかに接続で
きることは明らかだろう。
しかし、この知識がなければ、「正八面体の一つの面に正四面体が滑らかに接続できるか」
という疑問が起こるのは自然なことだろう。一般には自信がないのが普通だろう。
空間把握がしっかりしていないと、正八面体の面と正四面体の面が一体となって一つの面
を作るという保証が全くないことに気づかされる。
このことを計量的に示すには、次のように行えばよい。
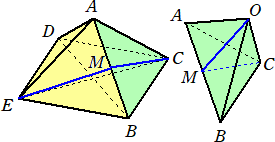
正八面体の上側の部分Ａ-ＢＣＤＥに対して、面ＡＢＣに正四面体ＯＡＢＣを貼り付けること
を考える。１辺の長さは２とする。
このとき、辺ＡＢの中点Ｍに対して、 ＭＣ＝ＭＥ＝
、ＣＥ＝２
なので、ｃｏｓ∠ＣＭＥ＝（３＋３−８）/６＝−１/３ である。
これに対して、 ＭＣ＝ＭＯ＝
、ＯＣ＝２ なので、ｃｏｓ∠ＯＭＣ＝（３＋３−４）/６＝１/３ である。
よって、ｓｉｎ∠ＣＭＥ＝２
/３、ｓｉｎ∠ＯＭＣ＝２/３ なので、加法定理より、ｃｏｓ（∠ＯＭＣ＋∠ＣＭＥ）＝（１/３）（−１/３）−（２
/３）（２/３）＝−１/９−８/９＝−１なので、 ∠ＯＭＣ＋∠ＣＭＥ＝π すなわち、３点 Ｏ、Ｍ、Ｅ は１直線上にある。
このことから、 △ＡＥＢの面と△ＯＡＢの面は、同一平面上にあることが分かる。
上記のような計算をしなくても、次のように考えれば自明だろう。
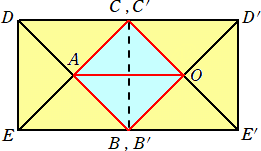
正八面体を横に並べると、 ＯＡ＝ＯＢ＝ＯＣＡＢ＝ＢＣ＝ＣＡ＝２ なので、三角錐Ｏ-ＡＢＣ
は正四面体である。
明らかに、△ＡＥＢの面と△ＯＡＢの面は、同一平面上にあることが分かる。
（追記） 令和４年７月６日付け
次の正四面体をある平面で切断した立体の体積の計算は、ありふれた問題だろう。
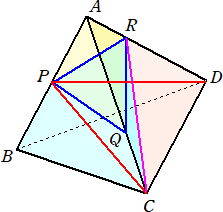
問 題 １辺の長さが３の正四面体ＡＢＣＤにおいて、下図のように辺上に４点Ｐ、Ｑ、Ｒ、
Ｓをとる。４点Ｐ、Ｑ、Ｒ、Ｓを通る平面で正四面体ＡＢＣＤを切断するとき、２つの立
体に分かれる。
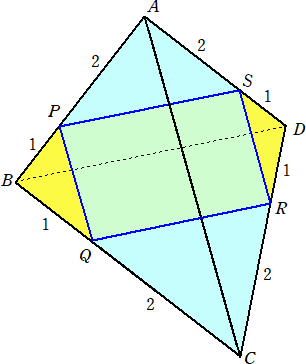
このとき、頂点Ａを含む方の立体の体積を求めよ。
（解） 求める立体は、四角錐ＡＰＱＲＳ＋三角錐ＡＱＣＲである。辺ＢＤ、ＡＣの中点をそれぞ
れＭ、Ｎとおく。線分ＭＮと長方形ＰＱＲＳの交点をＬとおく。
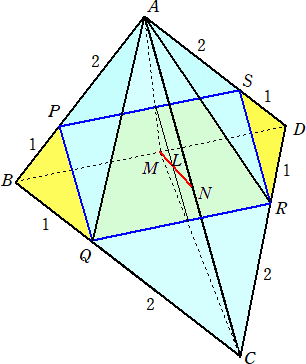
まず、長方形ＰＱＲＳの面積は、 １×２＝２
四角錐ＡＰＱＲＳの高さは、 （２/３）√｛（３
/２）2−（３/２）2｝＝よって、 四角錐ＡＰＱＲＳの体積は、 ２×
÷３＝（２/３）また、△ＱＣＲ＝（
/４）・２2＝ で、三角錐ＡＱＣＲの高さは、√｛３2−2｝＝なので、 三角錐ＡＱＣＲの体積は、
×÷３＝したがって、求める体積は、 （２/３）
＋＝（５/３） （終）（追記） 令和４年７月７日付け
上図において、正四面体に平面が交わり、辺ＡＢ、ＢＣ、ＣＤ、ＤＡとの交点Ｐ、Ｑ、Ｒ、Ｓに
ついて、
（ＡＰ/ＰＢ）（ＢＱ/ＱＣ）（ＣＲ/ＲＤ）（ＤＳ/ＳＡ）＝（２/１）（１/２）（２/１）（１/２）＝１
が成り立つ。上図は特別な場合（長方形ＰＱＲＳと辺ＡＣが平行）であったが、一般の場合に
も実は、
（ＡＰ/ＰＢ）（ＢＱ/ＱＣ）（ＣＲ/ＲＤ）（ＤＳ/ＳＡ）＝１
は成り立つ。この公式に関連する問題が、慶應義塾中等部の入試問題（２０１２）で出題さ
れている。次の問題は改題です。
問 題 １辺の長さが５の正四面体ＡＢＣＤがある。辺ＡＢ、ＣＤ、ＤＡ上に点Ｐ、Ｒ、Ｓがあり、
ＡＰ＝４、ＣＲ＝１、ＤＳ＝３で、この正四面体を３点Ｐ、Ｒ、Ｓを通る平面で切る切断面
がＢＣ上の点Ｑで交わるとき、ＢＱの長さを求めよ。
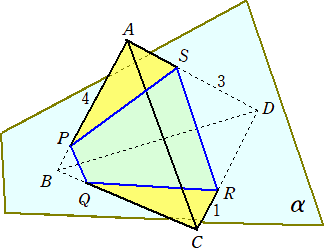
（解） ＢＱ＝ｘ とおくと、
（ＡＰ/ＰＢ）（ＢＱ/ＱＣ）（ＣＲ/ＲＤ）（ＤＳ/ＳＡ）＝（４/１）（ｘ/（５−ｘ））（１/４）（３/２）＝１
より、 ３ｘ＝１０−２ｘ なので、 ５ｘ＝１０ すなわち、 ｘ＝２ （終）
上記では、公式を用いて解いてしまったが、次のように地道に解くことも可能である。
（別解） 下図のように、直線ＳＰ、ＤＢ、ＲＱの交点をＴとおく。△ＡＢＤ上で、Ｓより辺ＤＢに
平行線を引き、辺ＡＢとの交点をＵとおく。同様に△ＢＣＤ上でＲより辺ＢＣに平行線を引き、
辺ＢＤとの交点をＶとおく。
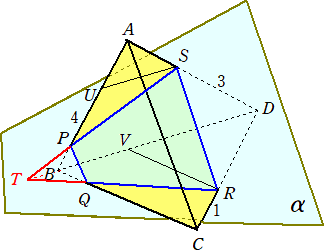
このとき、ＳＵ＝２ で、△ＰＳＵ∽△ＰＴＢ より、 ＴＢ ： ＳＵ＝１ ： ２ なので、 ＴＢ＝１
また、ＲＶ＝４ で、△ＴＱＢ∽△ＴＲＶ より、 ＴＢ ： ＴＶ＝ＢＱ ： ＲＶ なので、
ＢＱ ： ＲＶ＝１ ： ２
よって、 ＢＱ＝２ （終）
（追記） 令和４年７月８日付け
次の公式を証明しよう。
（公式） 下図のように正四面体ＡＢＣＤと平面αが交わる。辺ＡＢ、ＢＣ、ＣＤ、ＤＡと
の交点をそれぞれＰ、Ｑ、Ｒ、Ｓとすると、
（ＡＰ/ＰＢ）（ＢＱ/ＱＣ）（ＣＲ/ＲＤ）（ＤＳ/ＳＡ）＝１
が成り立つ。
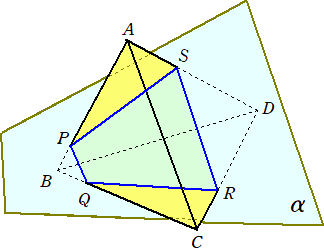
＃中学受験では、覚えておいて損はしない公式だろう。検算にも使えますね！
正四面体の頂点をグルリと（分子）、（分母）、（分子）、（分母）、・・・と唱えながら一周する
と覚えれば忘れないと思います。チェバの定理やメネラウスの定理と同じ覚え方です。
（証明） 下図のように、直線ＳＰ、ＤＢ、ＲＱの交点をＴとおく。
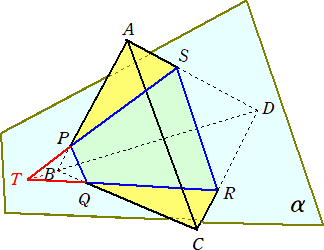
△ＡＢＤにおいて、メネラウスの定理より、 （ＡＰ/ＰＢ）（ＢＴ/ＴＤ）（ＤＳ/ＳＡ）＝１
△ＢＣＤにおいて、メネラウスの定理より、 （ＢＱ/ＱＣ）（ＣＲ/ＲＤ）（ＴＤ/ＢＴ）＝１
２式を辺々掛けて、 （ＡＰ/ＰＢ）（ＢＱ/ＱＣ）（ＣＲ/ＲＤ）（ＤＳ/ＳＡ）＝１ が成り立つ。 （終）
下図のように、正四面体ＡＢＣＤを底面ＢＣＤに平行な平面で切断するとき、
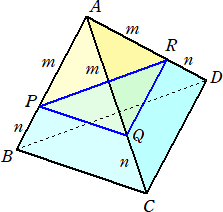
体積比は、相似比の３乗に比例するので、
正四面体ＡＰＱ ： 正四面体ＡＢＣ＝ｍ3 ： （ｍ＋ｎ）3
が成り立つ。
問題 下図のように、正四面体ＡＢＣＤにおいて、３辺ＡＢ、ＡＣ、ＡＤを３等分する点をＰ1、
Ｐ2、Ｑ1、Ｑ2、Ｒ1、Ｒ2とする。
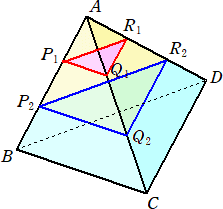
このとき、 正四面体ＡＰ1Ｑ1Ｒ1：三角錐台Ｐ1Ｑ1Ｒ1Ｐ2Ｑ2Ｒ2：三角錐台Ｐ2Ｑ2Ｒ2ＢＣＤ
の値を求めよ。
（解） 体積比は、相似比の３乗に比例するので、
正四面体ＡＰ1Ｑ1Ｒ1 ： 正四面体ＡＰ2Ｑ2Ｒ2 ： 正四面体ＡＢＣＤ＝１ ： ８ ： ２７
よって、
正四面体ＡＰ1Ｑ1Ｒ1：三角錐台Ｐ1Ｑ1Ｒ1Ｐ2Ｑ2Ｒ2：三角錐台Ｐ2Ｑ2Ｒ2ＢＣＤ＝１ ： ７ ： １９
である。 （終）
（追記） 令和４年７月９日付け
正四面体の底面に平行な平面で切断するときは、相似の公式が使えて簡便に求められる
が、一般の場合はどうだろうか？次の問題を考えてみよう。
問 題 １辺の長さが６の正四面体ＡＢＣＤがある。辺ＡＢ上にＡＰ＝３となる点Ｐをとり、辺
ＡＣ上にＡＱ＝４となる点Ｑをとり、辺ＡＤ上にＡＲ＝２となる点Ｒをとる。
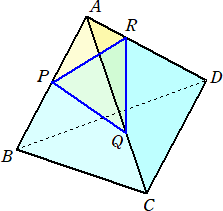
このとき、四面体ＡＰＱＲと正四面体ＡＢＣＤの体積比を求めよ。
（解）
上図において、 正四面体ＣＡＢＤ ： 四面体ＣＡＰＤ＝２ ： １
四面体ＣＡＰＤ ： 四面体ＣＡＰＲ＝３ ： １
四面体ＣＡＰＲ ： 四面体ＱＡＰＲ＝３ ： ２
なので、
四面体ＱＡＰＲ＝（２/３）四面体ＣＡＰＲ＝（２/３）（１/３）四面体ＣＡＰＤ
＝（２/３）（１/３）（１/２）正四面体ＣＡＢＤ
すなわち、 四面体ＡＰＱＲ＝（１/９）正四面体ＡＢＣＤ より、
四面体ＡＰＱＲ ： 正四面体ＡＢＣＤ＝１ ： ９ （終）
一般に、次の公式が成り立つ。証明は、上記の解と同様にすればよい。
（公式） 下図のように正四面体ＡＢＣＤの３辺上に３点Ｐ、Ｑ、Ｒをとる。
０＜ｂ、ｃ、ｄ＜１に対して、ＡＰ＝ｂ・ＡＢ、ＡＱ＝ｃ・ＡＣ、ＡＲ＝ｄ・ＡＤ とする。
このとき、 四面体ＡＰＱＲ ： 正四面体ＡＢＣＤ＝ｂｃｄ ： １ が成り立つ。
この公式を用いれば、上記の問題
問題 下図のように、正四面体ＡＢＣＤにおいて、３辺ＡＢ、ＡＣ、ＡＤを３等分する点をＰ1、
Ｐ2、Ｑ1、Ｑ2、Ｒ1、Ｒ2とする。
このとき、 正四面体ＡＰ1Ｑ1Ｒ1 ： 正四面体ＡＰ2Ｑ2Ｒ2 ： 正四面体ＡＢＣＤ の値を求めよ。
に対しても、次のように解いてもいいだろう。
（解） 公式より、
正四面体ＡＰ1Ｑ1Ｒ1 ： 正四面体ＡＰ2Ｑ2Ｒ2 ： 正四面体ＡＢＣＤ
＝（１/３）3 ： （２/３）3 ： １＝１/２７ ： ８/２７ ： １＝１ ： ８ ： ２７ （終）
（追記） 令和４年７月１１日付け
次の問題は、福島県公立高校入試（２０１９）で出題されたものである。超難問という噂で、
正答率がほとんど０％だったとか．．．。問題は、若干改題しました。
問題 １辺の長さが６の正四面体ＯＡＢＣがある。辺ＢＣの中点をＭとし、辺ＯＣを １ ： ２
に内分する点をＤとおく。辺ＯＢ上に点Ｅを、ＡＥ＋ＥＤが最小となるようにとる。
線分ＯＭとＤＥの交点をＰとする。線分ＡＭを ８ ： ７ に内分する点をＱとし、平面ＡＥＤと
直線ＯＱの交点をＲとおく。
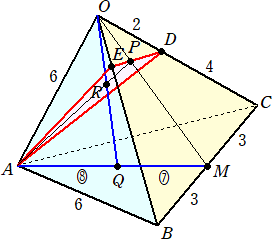
このとき、三角錐ＲＱＢＣの体積は、正四面体ＯＡＢＣの体積の何倍であるか？
（解） まず、ＯＰ ： ＰＭ を求める。
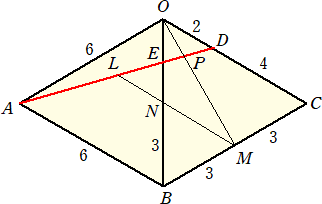
上図において、辺ＯＢの中点をＮとし、直線ＭＮと線分ＡＤの交点をＬとおく。
このとき、 △ＯＥＤ∽△ＢＥＡ なので、 ＯＥ ： ＥＢ＝１ ： ３
よって、 ＯＥ＝６×（１/４）＝３/２ 、ＥＢ＝６−３/２＝９/２ で、ＮＢ＝３ より、ＥＮ＝３/２
このとき、 ＯＥ ： ＥＮ＝１ ： １ から、 △ＯＥＤ≡△ＮＥＬ より、 ＬＮ＝２ となる。
中点連結定理より、 ＮＭ＝３ なので、 ＬＭ＝５ となる。
△ＯＰＤ∽△ＭＰＬ なので、 ＯＰ ： ＰＭ＝ＯＤ ： ＬＭ＝２ ： ５
次に、平面ＯＡＭにおいて、点Ｐより線分ＡＭに平行線を引き、線分ＯＱとの交点をＳとおく。
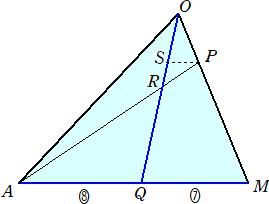
△ＯＳＰ∽△ＯＱＭ なので、 ＯＳ ： ＯＱ＝ＯＰ ： ＯＭ＝２ ： ７
このとき、 △ＳＰＲ∽△ＱＡＲ なので、 ＳＲ ： ＲＱ＝ＳＰ ： ＱＡ＝２ ： ８＝１ ： ４
以上から、 ＯＲ ： ＯＱ＝３ ： ７ より、 ＲＱ＝（４/７）ＯＱ となる。
よって、 （三角錐ＯＱＢＣの体積）＝（７/１５）×（正四面体ＯＡＢＣの体積）
（三角錐ＲＱＢＣの体積）＝（４/７）×（三角錐ＯＱＢＣの体積）
より、 （三角錐ＲＱＢＣの体積）＝（４/１５）×（正四面体ＯＡＢＣの体積） なので、
三角錐ＲＱＢＣの体積は、正四面体ＯＡＢＣの体積の４/１５倍である。 （終）
（コメント） 四面体ＯＡＢＣの体積は、 （
/１２）×６3＝１８ なので、三角錐ＲＱＢＣの体積は、 １８
×（４/１５）＝（２４/５） となる。（追記） 令和４年７月１３日付け
一般の四面体ＯＡＢＣにおいて、その重心Ｇは、底面の△ＡＢＣの重心Ｈと頂点Ｏを結ぶ
線分ＯＨを ３ ： １ に内分する点で定められるが、ねじれの位置にある辺同士の中点を結
ぶ線分の交点（互いの中点で交わる）としても定められる。（下図参照）
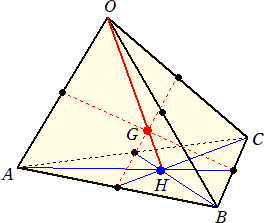
このことは、
ＯＧ＝（ＯＡ＋０Ｂ＋ＯＣ）/４
＝（（１/２）ＯＡ＋（０Ｂ＋ＯＣ）/２）/２
＝（（ＯＡ＋０Ｂ）/２＋（１/２）ＯＣ）/２
＝・・・
等から分かるだろう。
そこで、１辺の長さが ａ の正四面体ＯＡＢＣにおいて、ねじれの位置にある辺同士の中点
を結ぶ線分の長さを求めることを次に考えよう。
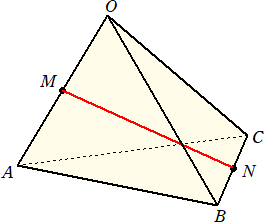
（解） ２点Ａ、Ｎを結び、直角三角形ＡＮＭを考える。
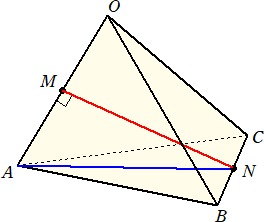
このとき、 ＡＭ＝ａ/２ 、 ＡＮ＝（
/２）ａ から、三平方の定理より、ＭＮ2＝（
/２）2ａ2−ａ2/４＝ａ2/２よって、 ＭＮ＝（
/２）ａ となる。 （終）ここで留意すべき点は、 ＭＮ＜ａ が成り立つということだろう。ＭＮの長さは、正四面体
の１辺の長さよりも短いという点が面白い。
（追記） 令和４年７月１４日付け
ねじれの位置にある２直線ＯＡとＢＣについて、ＭＮは最短の距離を与える。
最短であることから、 ＯＡ⊥ＭＮ 、ＢＣ⊥ＭＮ が成り立つ。
いま、線分ＯＡを ｔ ： １-ｔ に内分する点をＰ、線分ＢＣを ｓ ： １-ｓ に内分する点をＱとする
と、
ＯＰ＝ｔＯＡ 、 ＯＱ＝（１-ｓ）ＯＢ＋ｓＯＣ より、 ＰＱ＝（１-ｓ）ＯＢ＋ｓＯＣ−ｔＯＡ
ＰＱが最短の距離を与えるとき、 ＯＡ⊥ＰＱ 、ＢＣ⊥ＰＱ なので、
（（１-ｓ）ＯＢ＋ｓＯＣ−ｔＯＡ）・ＯＡ＝｛（１-ｓ）/２＋ｓ/２−ｔ｝ａ2＝０ より、 ｔ＝１/２
（（１-ｓ）ＯＢ＋ｓＯＣ−ｔＯＡ）・（ＯＣ−ＯＢ）
＝（１-ｓ）/２−（１-ｓ）＋ｓ−ｓ/２−ｔ/２＋ｔ/２）ａ2＝０ より、 ｓ＝１/２
よって、確かに最短の距離を与える２点は、Ｍ、Ｎであることが分かる。
若干、Ｍの位置をずらした問題を考えよう。
問 題 １辺の長さが４の正四面体ＯＡＢＣにおいて、辺ＯＡを ３ ： １ に内分する点をＰ、
辺ＢＣの中点をＮとする。
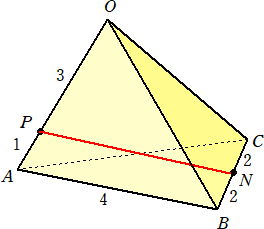
このとき、線分ＰＮの長さを求めよ。
（解） 直角三角形ＰＢＮを考える。（以下の解答は、ＭＮを求める問題の別解となる。）
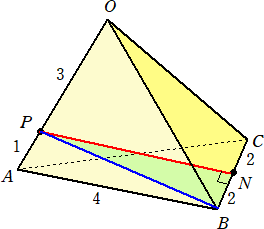
余弦定理より、 ＰＢ2＝１2＋４2−２・１・４・ｃｏｓ６０°＝１３ なので、
ＰＮ2＝１３−４＝９ より、 ＰＮ＝３ （終）
（コメント） 上記の問題設定で、△ＯＰＮが２等辺三角形になる点に興味が引かれた。
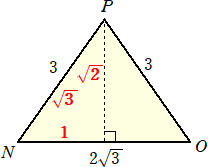
均整のとれた２等辺三角形ですね！
（追記） 令和４年７月１５日付け
（公式） １辺の長さが ａ の正四面体ＯＡＢＣにおいて、ねじれの位置にある辺同士の
中点Ｍ、Ｎを結ぶ線分の長さＭＮは、ＭＮ＝（
/２）ａ で与えられる。この公式を用いれば、ＭＮの長さが任意に与えられたとき、正四面体の１辺の長さを瞬時
に求めることが出来る。公式として知っていれば、便利かも．．．！
例 ＭＮ＝４のとき、正四面体の１辺の長さは、４
である。このＭＮに関する問題をもう１題あげておこう。
問 題 １辺の長さが ａ の正四面体ＯＡＢＣにおいて、ねじれの位置にある辺ＯＡ、ＢＣの
中点をそれぞれＭ、Ｎとおく。また、辺ＡＢの中点をＬとおく。
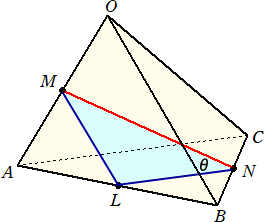
このとき、∠ＬＮＭの大きさ（＝θ）を求めよ。
（解） △ＬＮＭは、ＬＮ＝ＬＭ＝ａ/２ 、ＭＮ＝（
/２）ａ の２等辺三角形である。よって、 ｃｏｓθ＝（
/４）ａ÷（ａ/２）＝１/ より、 θ＝４５° となる。 （終）（コメント） 上記の計算結果から、∠ＭＬＮ＝９０° となり、△ＬＮＭは、直角２等辺三角形
になるんですね！これは美しい．．．。でも、このことは当たり前ですね。なぜなら
ば、３点Ｌ、Ｍ、Ｎを通る平面で正四面体を切断するとき、その切り口は正方形な
んだもの．．．。
（追記） 令和４年７月１６日付け
立体図形の問題で、「そんな風に考えるんだ．．．。」という問題を紹介しよう。問題解法の
視点として身につけた方がよい考え方だと思う。
次は、豊島岡学園中学の入試問題（２０２２）である。問題は若干改題しました。
問 題 １辺の長さが６の正四面体２つを上下に重ねた立体図形Ｏ-ＡＢＣ-Ｏ’がある。
ＯＡ、Ｏ’Ｂを １ ： ２ に内分する点をそれぞれＰ、Ｑとおく。辺ＡＢの中点をＭとし、
線分ＣＭと線分ＰＱの交点をＲとおく。
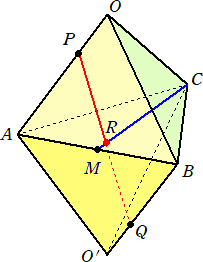
このとき、ＭＲ ： ＲＣ を求めよ。
（解） Ｏ、Ｏ’より平面ＡＢＣに垂線を下ろし、その足をＧとおくと、Ｇは△ＡＢＣの重心である。
同様に、Ｐ、Ｑより平面ＡＢＣに垂線を下ろし、その足をそれぞれＰ’、Ｑ’とおく。
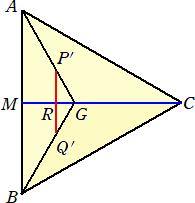
このとき、 ＭＣ＝（
/２）×６＝３ で、 ＭＧ＝３×（１/３）＝ＭＲ ： ＲＧ＝ＡＰ’ ： Ｐ’Ｇ＝２ ： １ なので、 ＭＲ＝（２/３）ＭＧ＝（２/３）
また、 ＲＣ＝３
−（２/３）＝（７/３） なので、 ＭＲ ： ＲＣ＝２ ： ７ （終）（追記） 令和４年８月７日付け
下図のように、１辺の長さが２の正三角形ＡＢＣの外側に、１辺の長さが２の正三角形を貼
り付ける。その頂点を結ぶ三角形ＰＱＲは、明らかに、１辺の長さが４の正三角形となる。
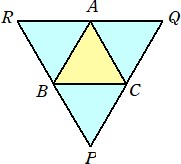
この話題を正四面体の場合に考えよう。
１辺の長さが２の正四面体ＯＡＢＣの外側に、１辺の長さが２の正四面体を貼り付ける。
その頂点を結ぶ三角錐は、明らかに、正四面体である。
この正四面体の１辺の長さは、いくらになるのだろうか？
正四面体ＯＡＢＣにおいて、辺ＯＡの中点Ｍを通り、辺ＢＣを含む平面で切断する。その切
断面は、下図のようになる。
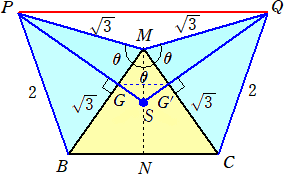
上図において、Ｎは辺ＢＣの中点、Ｇ、Ｇ’はそれぞれ△ＯＡＢ、△ＯＡＣの重心で、直線ＰＧ
と直線ＰＧ’の交点をＳとおく。Ｓは線分ＭＮ上の点である。
θは、正四面体の隣り合う面のなす角で、ｃｏｓθ＝１/３ である。
ＭＧ＝ＭＧ’＝
/３ なので、余弦定理より、ＧＧ’2＝（
/３）2＋（/３）2−２・（/３）2ｃｏｓθ＝４/９ から、 ＧＧ’＝２/３ＧＳ＝Ｇ’Ｓ＝ｘ とおいて、∠ＧＳＧ’＝π−θ から、余弦定理より、
ｘ2＋ｘ2−２ｘ2・ｃｏｓ（π−θ）＝（２/３）2 すなわち、 （８/３）ｘ2＝４/９
よって、 ｘ＝１/
となるので、 ＰＳ＝ＱＳ＝（２/３）＋（１/６）＝（５/６）以上から、余弦定理より、
ＰＱ2＝（（５/６）
）2＋（（５/６））2−２・（（５/６））2ｃｏｓ（π−θ）＝１００/９すなわち、求める正四面体の１辺の長さは、 ＰＱ＝１０/３ である。
（参考図） 立体を上から見た図
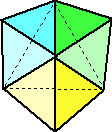
（コメント） ＭＧ＝
/３ 、 ＧＳ＝１/ より、三平方の定理より、 ＭＳ＝/２ここで、 ＭＮ＝
なので、ちょうど Ｓは線分ＭＮの中点であることが分かる。以下、工事中！
